Constante de raideur d'un ressort : bac S Amérique du Nord 2011.

. . . .

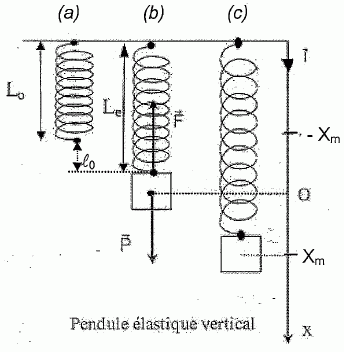
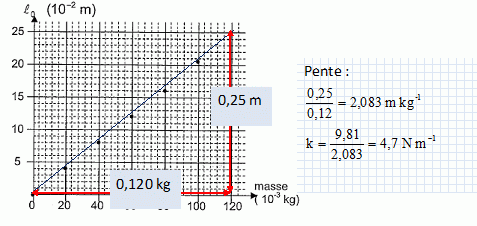
On dispose d'un pendule élastique vertical constitué d'un ressort de masse négligeable et de constante de raideur k, auquel on accroche un solide de masse m. Le ressort s'allonge de la longueur l0 : une position d'équilibre est atteinte. A partir de cette position d'équilibre, on étire le ressort verticalement puis on le lâche. Le système effectue des oscillations libres de part et d'aute de sa position d'équilibre avec une amplitude xm et une pseudo-période T. (a) ressort à vide  : longueur L0. (b) ressort à l'équilibre: phase sattique, longueur Lé. (c) ressort en oscillation: phase dynamique. La position du centre d'inertie du solide est repérée par son abscisse x dans le repère proposé. Intensité de la pesanteur g =9,81 N / kg. Etude statique. On mesure l'allongement pour différentes valeur de m.  masse m (10-3 kg) 20 40 60 80 100 allongement l0 (10-2 m) 4,0 8,1 12,2 16,2 20,2 Exprimer l'allongement en fonction de L0 et Le. l0 = Le-L0. Etablir la relation entre m, g, k et l0 à l'équilibre. 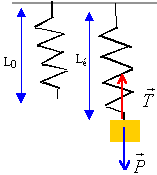La masse m est soumise à son poids et à la tension du ressort. A l'équilibre ces deux forces sont opposées. A l'équilibre : mg = k(Lé-L0) ;  l0 = mg  /k. Déterminer graphiquement  la constante de raideur k. 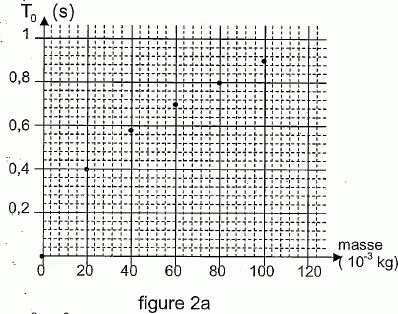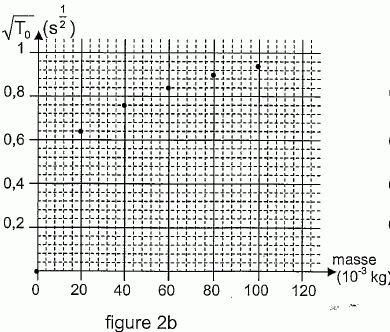Etude dynamique. Pour les mêmes valeurs de la masse m, on mesure avec un chronomètre la durée de 10 oscillations. masse m ( 10-3 kg) 20 40 60 80 100 durée de 10 oscillations (s) 4,06 5,75 6,95 8,03 8,96 Pour un oscillateur non amorti, l'équation différentielle vérifiée par l'abscisse x du centre d'inertie du solide S s'écrit : m x" + kx=0. 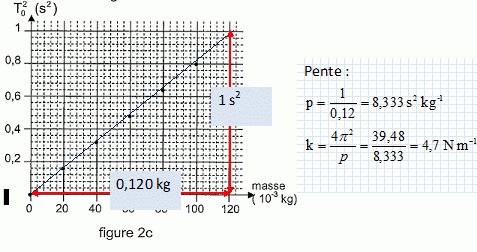La solution de cette équation, dans le cas présent, est x = xm cos (2p t / T0). Que représente T0 ? T0 est la période propre de l'oscillateur libre non amorti.  Montrer que T0 = 2 p(m/k)½. 2p / T0 = w0, pulsation en rad / s.  De plus x" + k/ m x= ; on pose  w02 = k / m. Par suite 2p / T0 =(k / m)½ soit T0 = 2p (m / k)½. En réalité, l'amplitude du mouvement ne reste pas constante. Le mouvement est qualifié de pseudo-périodique. Comment évolue l'amplitude du mouvement au cours du temps ? Comment le justifier ? L'amplitude diminue au cours du temps. L'énergie mécanique de l'oscillateur diminue du travail des frottements. A quelle condition, la pseudo-période T est-elle très proche de T0 ? L'amortissement doit être faible. On considère, dans la suite, que cette condition est vérifiée. Comment procéder pour que la mesure de T soit la plus précise possible ? On mesure non pas la durée d'une seule oscillation, mais la durée d'une dizaine d'oscillations, puis on divise cette durée par 10. Choisir l'une des représentation fournies pour déterminer la valeur de k puis la calculer. T0 = 2p (m / k)½ ; T02 = 4p2 / k m   ; T02 est proportionnellle à la masse m. ( figure (c)).  La pente de la droite est égale à 4p2 / k.

menu