Etude d'une bobine, montage transmetteur Pt 100: bac Stl 2008 Antilles.

. . . .

Etude d'une bobine. Cette étude est menée à partir de trois expériences utilisant une même bobine, de résistance interne R et d’inductance L. Expérience 1 : la bobine est alimentée par un générateur de tension continue. Un ampèremètre indique un courant d’intensité I1 = 30 mA et un voltmètre indique aux bornes de la bobine une tension U1 = 6,2 V. 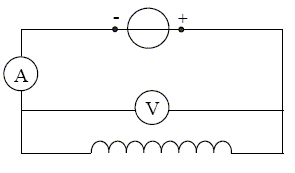Déterminer la valeur de la résistance interne R de la bobine. Tension aux bornes de la bobine U1 =RI1 ; R = U1 / I1 =6,2 /0,030 = 206,66 ~2,1 102 ohms. Expérience 2 : le générateur de l’expérience 1 est remplacé par un générateur délivrant une tension sinusoïdale alternative de fréquence f = 50 Hz. Les appareils de contrôle, en position AC, affichent alors les valeurs efficaces suivantes : I2 = 13 mA, U2 = 5,2 V. 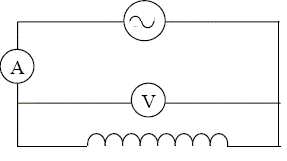Calculer la valeur de l’impédance Z de la bobine. Tension aux bornes de la bobine U2 =Z I2 ; Z = U2 / I2 = 5,2 /0,013 = 400 ~4,0 102 ohms. En déduire la valeur de l’inductance L de la bobine.. Z2 = R2+(Lw)2 avec w = 2*3,14*50 = 314 rad/s. (Lw)2 = Z2 - R2 = 4002-206,662 =1,173 105 ; Lw =(1,173 105)½=3,42 102 ohms ; L =342/314 =1,09 ~1,1 H. Expérience 3 : On reprend le montage de l’expérience 2 enplaçant en série avec la bobine un condensateur de capacité réglable C. Le réglage du générateur étant conservé, on fait varier la valeur de C. L’intensité efficace mesurée varie ; elle passe par un maximum pour une valeur de la capacité C0 = 9,2 μF. 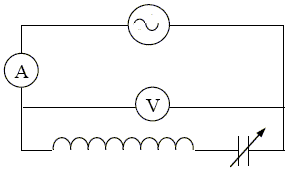Nommer le phénomène observé lors de la troisième expérience. On observe le phénomène de résonance d'intensité. Indiquer la valeur de l’impédance du dipôle RLC lorsque la valeur efficace de l’intensité I passe par un maximum. En déduire la relation entre L, C0 et la pulsation ω dans ce cas. A la résonance d'intensité, l'impédance est minimale, égale à la résistance R du dipôle RLC. On rappelle l’expression de l’impédance d’un dipôle RLC : 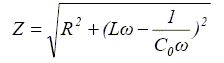Lw -1/(C0w)=0 ; LC0w2=1. En déduire la valeur de l’inductance L de la bobine. Comparer ce résultat à la valeur de L obtenue à partir de l’expérience 2. L =1 /(C0w2) = 1 / (9,2 10-6 *3142) = 1,10 ~1,1 H, valeur identique à 1% près. Présentation du montage transmetteur Pt 100. La sonde de température Pt 100 est couramment utilisée dans l’industrie chimique. Elle est constituée d’un mince fil de platine dont la résistance RPt varie avec la température et qui peut s’exprimer sous la forme : RPt = 100 + a × θ RPt : résistance du fil de platine (en Ω ) θ : température (en °C) a : coefficient appelé sensibilité de la sonde (en Ω. 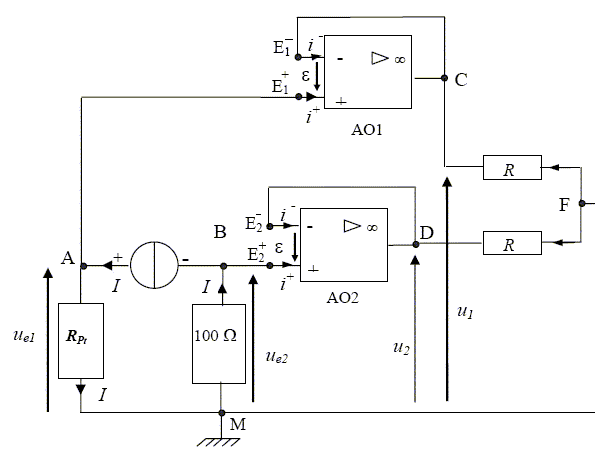°C-1)   Le rôle du montage transmetteur : La sonde étant placée à une extrémité du montage transmetteur, on désire avoir à l’autre extrémité une tension de sortie uS dont la valeur en volt s’exprime numériquement sous la forme : uS = 10-3 × θ (uS en volt et θ en degré Celsius) Pour cela, la sonde est placée dans la maille AMBA qui comporte un générateur de courant délivrant un courant d’intensité I et un conducteur ohmique de résistance égale à 100 Ω. Calculer en millivolt la valeur de uS pour une température de 110 °C. Expliquer l’intérêt de ce montage. uS = 10-3 × θ  = 110 10-3 = 0,11 V = 110 mV. Les quatre amplificateurs présents dans le montage schématisé  fonctionnent en régime linéaire. Rappeler les hypothèses simplificatrices concernant un amplificateur opérationnel supposé idéal fonctionnant en régime linéaire. Les deux entrées sont au même potentiel : e = 0. Les intensités des courants dans les deux entrées sont nulles. L’intensité I du courant est la même dans toute la maille AMBA (démonstration non demandée). Comparer les signes des tensions ue1 et ue2. ue1 + ue2 =0 ; ue1 =- ue2 .  Exprimer la tension ue1 en fonction de a, θ et I. ue1 = RPt I =(100+ a q) I. Exprimer la tension ue2 en fonction de I. ue2 = -100 I. Étude de la partie gauche du montage (A.O.1 et A.O.2) Nommer le type de montage des amplificateurs opérationnels A.O.1 et A.O.2. Montage suiveur de tension. Donner la relation existant entre ue1 et u1. Même question pour ue2 et u2. ue1 = u1 ; ue2 =  u2.  Exprimer u1 en fonction de a, θ et I. Exprimer u2 en fonction de I. u1 = (100+ a q) I ; u2 = -100 I. 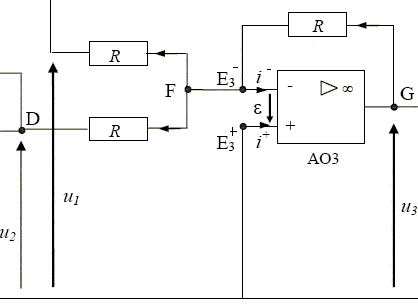Étude de la partie centrale du montage (A.O.3). Les trois résistances R étant identiques, on reconnaît un montage additionneur (sommateur) inverseur. La relation entre les tensions est : u3 = - ( u1 + u2 ) Montrer que u3 = - a × θ × I. 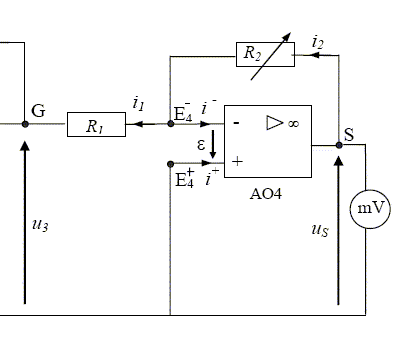u3 = - ( u1 + u2 ) = -((100+ a q) I- 100 I) = - a × θ × I. Étude de la partie droite du montage (A.O.4) En utilisant la loi des mailles et la loi des noeuds, établir l’expression de uS en fonction de u3 , R1 et R2. Donner le nom de ce montage. Au noeud E-4 : i2 = i1 +i- avec i- =0 d'où i1 = i2. E+4 est relié à la masse ; E+4 =E+4 =0. u3 = -R1i1 soit : i1 = -u3 /R1  ; us = R2i2  = R2i1  = - R2 / R1 u3 ; montage amplificateur inverseur.  Exprimer uS en fonction de a, θ, I, R1 et R2. us = - R2 / R1 (- a × θ × I) us =  R2 / R1 a q I. Conclusion. On donne les valeurs suivantes : I = 1,00 mA, a = 0,385 Ω.°C-1, R1 = 500 Ω Déterminer la valeur à donner à la résistance réglable R2 pour que la tension uS soit numériquement égale à 10-3 × θ (uS en volt et θ en degré Celsius) us =  R2 / R1 a q I. R2  = us R1 / (a q I) = 10-3 R1 / (a  I). R2  =10-3 *500 / (0,385*1,00 10-3) =500/0,385 = 1,3 103 ohms.

menu