Hydrométallurgie du zinc, dosage du cuivre dans un laiton : bac STL chimie de laboratoire 2011

Aurélie 08/09/11

Hydrométallurgie du zinc, dosage du cuivre dans un laiton : bac STL chimie de laboratoire 2011.

. .

.
.

Le zinc métallique est obtenu à partir de la blende, minerai essentiellement constitué de sulfure de zinc, avec notamment des traces d’oxyde de cuivre(II).
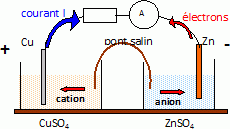
Après plusieurs étapes de traitement de la blende, on obtient une solution aqueuse S contenant des ions Zn²⁺ et des traces d’ions Cu²⁺.
Les concentrations molaires sont égales à 2,3 mol.L^-1 pour les ions Zn²⁺ et 1,6 x 10^-2 mol.L^-1 pour les ions Cu²⁺ dans la solution S.
L’objectif est d’éliminer les ions cuivre(II) de la solution S.
Étude d’une pile.
Dans un bécher 1, on place un volume V₁ = 100 mL d’une solution S₁ de sulfate de cuivre(II) de concentration molaire c₁ = 1,6 x 10^-2 mol.L^-1.
Dans un bécher 2, on place un volume V₂ = 100 mL d’une solution S₂ de sulfate de zinc de concentration molaire c₂ = 2,3 mol.L^-1.
Étude de la demi-pile 1.
On plonge une lame de cuivre dans le bécher 1.
Donner l’expression littérale du potentiel E₁ de l’électrode de cuivre plongeant dans la solution S₁.
Calculer le potentiel de cette électrode.
E₁ = E°(Cu²⁺aq/Cu(s)) + 0,03 log [Cu²⁺aq] =0,34 +0,03 log 1,6 x 10^-2 = 0,286 ~0,29 V.
Étude de la demi-pile 2.
Donner l’expression littérale du potentiel E₂ de l’électrode de zinc plongeant dans la solution S₂.
Calculer le potentiel de cette électrode.
E₂ = E°(Zn²⁺aq/Zn(s)) + 0,03 log [Zn²⁺aq] = -0,76 +0,03 log 2,3= -0,749 ~ -0,75 V.

Étude de la pile obtenue en reliant la demi-pile 1 à la demi-pile 2.
Faire un schéma annoté de cette pile : indiquer les polarités et préciser le sens de circulation des électrons et du courant.

Calculer la force électromotrice de cette pile en début de fonctionnement.
E = E₁ -E₂ =0,286+0,749 =1,03 V.

Étude de l’évolution du système.
Écrire l’équation de la réaction modélisant la transformation qui se produit dans la pile lorsqu’elle débite.
Zn(s) + Cu²⁺aq = Cu(s) + Zn²⁺aq.
Donner l’expression de la constante d’équilibre K de la réaction mise en jeu en fonction des concentrations des différentes espèces à l’équilibre.
K = [Zn²⁺aq]_éq / [Cu²⁺aq]_éq
Établir l’expression de la constante d’équilibre K en fonction des potentiels standard des couples mis en jeu ; vérifier que cette constante est voisine de 5 x 10³⁶.
A l'équilibre E₁ = E₂ : E°(Cu²⁺aq/Cu(s)) + 0,03 log [Cu²⁺aq] = E°(Zn²⁺aq/Zn(s)) + 0,03 log [Zn²⁺aq]
E°(Cu²⁺aq/Cu(s))-E°(Zn²⁺aq/Zn(s)) = 0,03 log([Zn²⁺aq] / [Cu²⁺aq])
( E°(Cu²⁺aq/Cu(s))-E°(Zn²⁺aq/Zn(s)) ) / 0,03 = ln K.
log K =(0,34 +0,76)/0,03 =36,67 ; K = 4,6 10³⁶.
Exprimer et calculer le quotient de réaction Q_r,i en début de fonctionnement. En déduire le sens d’évolution du système constitué par la pile.
Q_r,i = [Zn²⁺aq]_i / [Cu²⁺aq]_i =2,3 / 1,6 10^-2 =1,4 10².
Q_r,i < K, donc évolution spontanée dans le sens direct.
Calculer la concentration en ions cuivre(II) dans le bécher 1 quand la pile s’arrête de fonctionner (on considèrera que la concentration dans le bécher 2 reste sensiblement égale à
c₂ tout au long de la transformation).
K = [Zn²⁺aq]_éq / [Cu²⁺aq]_éq = c₂ / [Cu²⁺aq]_éq ; [Cu²⁺aq]_éq = c₂ / K = 2,3 / 4,6 10³⁶ =5 10^-37 mol/L.
La cémentation.
La cémentation consiste à disperser de la poudre de zinc dans la solution S contenant des ions
Cu²⁺ et Zn²⁺. Après plusieurs heures de contact, la solution est filtrée.
Expliquer l’intérêt de cette opération de cémentation.
Le zinc solide est oxydé en ion zinc(II), tandis que les ions cuivre (II) sont réduits en cuivre solide ; ces derniers se déposent au fond de la solution. D'après le calcul précédent, pratiquement tous les ions cuivre (II) sont éliminés de la solution.

Dosage du cuivre dans un laiton.
Le laiton est un alliage constitué de cuivre et de zinc. Sa teneur en cuivre est comprise entre 95 % et 55 %, en masse.
La teneur en cuivre dans un laiton peut être déterminée par spectrophotométrie d’absorption du complexe [Cu(NH₃)₄]²⁺.
Dans un premier temps, le laiton est attaqué par une solution d’acide nitrique. Après neutralisation et dilution, on obtient une solution contenant des ions cuivre(II). Les ions cuivre(II) sont ensuite complexés par l’ammoniac, à l’aide d’une solution tampon ammoniacale.
Attaque du laiton.
Écrire l’équation de la réaction d’oxydation du cuivre avec les ions nitrate de la solution d’acide nitrique (les demi-équations d’oxydo-réduction sont demandées).
L'ion nitrate, en milieu acide constitue l'oxydant le plus fort ; le zinc et le cuivre sont des réducteurs capables d'être oxydés par cet ion nitrate.
2NO₃^- + 8H⁺ + 6 e^- = 2 NO + 4 H₂O réduction
3Zn = 3Zn²⁺ + 6 e^- oxydation
3Cu = 3Cu²⁺ + 6 e^- oxydation
2NO₃^- + 8H⁺ +3Zn = 3Zn²⁺ +2 NO + 4 H₂O (2)
ou 8(NO₃^- + H⁺ ) +3Zn = 3(Zn²⁺ + 2NO₃^- )+2 NO + 4 H₂O (2)
2NO₃^- + 8H⁺ +3Cu = 3Cu²⁺ +2 NO + 4 H₂O (1 )
ou 8(NO₃^- + H⁺ ) +3Cu = 3(Cu²⁺ + 2NO₃^- )+2 NO + 4 H₂O (1)
Étude d’une solution tampon.
On désire préparer V=500,0 mL d’une solution tampon de pH égal à 9,2 par dissolution d’une masse m de chlorure d’ammonium solide dans une solution d’ammoniac à 2,0 mol.L^-1 (la dissolution s’effectue sans variation de volume).
Rappeler les propriétés d’une solution tampon.
Une solution tampon modère les variations de pH suite à l'ajout modéré d'un acide fort ou d'une base forte. Le pH d'un solution tampon ne varie pas suite à une dilution modérée.
Calculer la concentration en ions ammonium dans la solution tampon à pH = 9,2.
Le pK_a du couple (NH₄⁺ / NH₃) est égl à 9,2. A pH=pK_a, la quantité de matière d'ammoniac est égale à celle d'ion ammonium. [NH₄⁺]=2,0 mol/L.
Calculer la masse m de chlorure d’ammonium solide à dissoudre.
En solution l'ammoniac réagit partiellement avec l'eau ; on peut considérer que les ion ammonium proviennent exclusivement du chlorure d'ammonium dissout.
n = [NH₄⁺] V = 2,0 *0,500 = 1,0 mol ; m = n M_NH4Cl = 1,0*53,5 = 53,5 g.

Formation du complexe [Cu(NH₃)₄] ²⁺.
Le complexe est formé en mélangeant la solution d’ions cuivre(II) et la solution tampon à pH = 9,2.
On obtient ainsi une solution de pH = 9,2 présentant une concentration initiale en ions cuivre(II) c_Cu = 0,010 mol.L^-1 et une concentration initiale en ammoniac c_NH3 égale à 2,0 mol.L^-1. Compte tenu du large excès d’ammoniac, on considérera que la concentration de cette espèce est constante.
Écrire l’équation de la réaction de complexation des ions cuivre(II) par l’ammoniac.
Cu²⁺ + 4NH₃ =[Cu(NH₃)₄] ²⁺.
Donner le nom du complexe formé.
Ion tétramminecuivre (II).
Donner l’expression littérale de la constante de dissociation de ce complexe.
K_D =[Cu²⁺][NH₃]⁴ / [[Cu(NH₃)₄] ²⁺]= 1,0 10^-12.
Au regard de la valeur de cette constante de dissociation, que peut-on dire de la stabilité du complexe formé et donc de la réaction de formation du complexe ?
K_D étant très faible, le complexe [Cu(NH₃)₄] ²⁺est très stable.
En déduire la concentration du complexe en solution.
[[Cu(NH₃)₄] ²⁺]~c_Cu = 0,010 mol.L^-1.

On traite une masse de 1,4 g d’un laiton.
Après attaque par la solution d’acide nitrique et complexation par le tampon ammoniacal, on obtient 200,0 mL de solution : la courbe d’étalonnage obtenue par spectrophotométrie d’absorption donne
une concentration en complexe [Cu(NH₃)₄] ²⁺ dans cette solution égale à 8,0 x 10^-2 mol.L^-1.
Calculer la masse de cuivre contenue dans l’échantillon de laiton traité.
n_Cu = n([Cu(NH₃)₄] ²⁺) = 0,200*8,0 x 10^-2 =0,016 mol ; m_Cu= n_Cu M_Cu =0,016*63,5 =1,016 ~1,02 g.
Déterminer alors le pourcentage massique en métal cuivre dans le laiton étudié ; vérifier que ce résultat est conforme avec les indications de l’énoncé sur la teneur générale en cuivre d’un laiton.
1,016/1,4 *100 =72,6 % ~73 %, valeur comprise entre 55 et 95 %. Le résultat est en accord avec l'énoncé.

menu