|
Les propriétés du cuivre : pile cuivre nickel, radioactivité d'un isotope du cuivre, principe de l'expérience de Cavendish : bac STL PLPI 2011. |
|||||||
|
|||||||
|
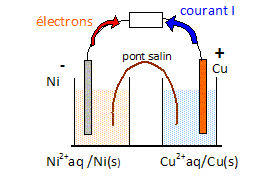
Ses propriétés permettent des utilisations variées : il a été utilisé dans la première pile électrique de Volta, actuellement dans les câbles électriques et les microprocesseurs. Les scientifiques ont réussi à obtenir des isotopes du cuivre utilisés dans le secteur de la médecine nucléaire (radiothérapie) grâce à leurs propriétés radioactives. Cette étude des propriétés du cuivre comporte deux parties indépendantes : A . Etude d’une pile (4,5 points) On se propose dans cette première partie d’étudier la propriété conductrice du cuivre naturel, dans le fonctionnement d’une pile cuivre – nickel. On prépare par dissolution : - Une solution (S1) de chlorure de nickel II de volume V1 = 250,0 mL et de concentration C1 = 0,216 mol. L-1, - Une solution (S2) de sulfate de cuivre II de volume V2 = 250,0 mL et de concentration C2 = 0,238 mol. L-1. Ecrire l’équation de dissolution du chlorure de nickel II dans l’eau. NiCl2(s) = Ni2+aq+2Cl-aq. Calculer la masse m1 de chlorure de nickel II solide à peser pour préparer la solution (S1). MNiCl2 = 129,6 g. mol-1. n = V1 C1 = 0,250 *0,216 =0,0540 mol ; m1= n MNiCl2 == 0,0540*129,6 = 6,998~7,00 g. Décrire le mode opératoire permettant de réaliser la solution (S1) de chlorure de nickel II en précisant la verrerie utilisée. Peser 7,00 g de solide :balance de précision, coupelle, spatule. Placer un entonnoir au dessus de la fiole jaugée de 250 mL, y verser le solide ; rincer coupelle et entonnoir à l'eau distillée. Remplir la fiole jaugée au 2/3 d'eau distillée, agiter jusqu'à dissolution complète. Compléter la fiole jaugée jusqu'au trait de jauge avec de l'eau distillée ; boucher, agiter pur rendre homogène. On réalise une pile « nickel-cuivre » en associant les deux demi-piles suivantes : · Demi-pile N° 1 : Electrode de nickel plongeant dans la solution de chlorure de nickel II (S1), · Demi-pile N° 2 : Electrode de cuivre plongeant dans la solution de sulfate de cuivre II (S2). Ecrire, pour chaque couple redox, la demi-équation correspondante. Ni2+aq + 2e- = Ni(s) ; E°(Ni2+aq /Ni(s) = -0,25 V. Cu2+aq + 2e- = Cu(s) ; E°(Cu2+aq /Cu(s) = +0,34 V. Calculer les potentiels E1 et E2 de chaque demi-pile. E1 =E°(Ni2+aq /Ni(s)+0,03 log [Ni2+aq] = -0,25 +0,03 log 0,216 = -0,27 V. E2 =E°(Cu2+aq /Cu(s)+0,03 log [Cu2+aq] = +0,34 +0,03 log 0,238 = 0,32 V. En déduire la force électromotrice de la pile en début de fonctionnement. E = E2 -E1 =0,32-(-0,27) =0,59 V. Faire le schéma annoté de la pile débitant dans un récepteur, en indiquant les polarités des électrodes, le sens de circulation des électrons et celui du courant.
Ni(s) + Cu2+aq = Ni2+aq + Cu(s). B . Radioactivité du cuivre. Dans cette partie on se propose d’étudier les propriétés radioactives d’un des isotopes artificiels du cuivre. Le cuivre naturel possède principalement deux isotopes 63Cu et 65Cu. Définir le terme « isotopes ». Deux isotopes ne diffèrent que par leur nombre de neutrons.Ils ont le même numéro atomique Z. Donner la composition du noyau 63Cu. On donne 27C0 ; 28Ni ; 29Cu ; 30Zn ; 31Ga ; 32Ge. 29 protons et 63-29 = 34 neutrons. Pour le traitement des cancers, on utilise l’isotope artificiel du cuivre 67Cu, émetteur β-, dont la période radioactive est suffisamment courte, ce qui permet aux patients de sortir rapidement après traitement. Préciser la nature de la particule émise lors d’une désintégration de type β-. Un électron noté 0-1e. S’agit-il d’une réaction nucléaire spontanée ou provoquée ? La réaction nucléaire est spontanée. Ecrire l’équation de la réaction de désintégration du nucléide 67Cu en précisant les lois utilisées. 2967Cu ---> ZAX + 0-1e. Conservation de la charge : 29 = Z-1 d'où Z =30 ( élément zinc ). Conservation du nombre de nucléons : 67=A. 2967Cu ---> 3067Zn + 0-1e. La période radioactive de l’isotope 67Cu est T = 62 h. Définir en une phrase la période radioactive. La demi-vie radioactive,(ou période) notée T, d'un échantillon de noyaux radioactifs est égale à la durée au bout de laquelle la moitié des noyaux radioactifs initiaux se sont désintègrés. Montrer que λ =ln2 / T. La loi de décroissance radioactive s'écrit N(t) = N0 exp(-l t ). N(T) =½N0 = N0exp(-l T ) ; 0,5 = exp(-l T ) ; ln 0,5 = -ln2 = -l T ; λ =ln2 / T. Calculer la valeur de la constante radioactive λ de 67Cu en précisant l’unité. l = ln2 / 62 = 0,01118 ~0,011 heure-1. Du cuivre 67Cu ayant été administré au patient, ce dernier est autorisé à sortir lorsque l’activité de l’isotope devient égale à 80 % de son activité initiale. Au bout de combien de temps le patient peut-il quitter l’hôpital ? 0,80 N0 = N0 exp(-l t ) ; 0,80 = exp(-l t ) ; ln 0,80 = -l t ; t =- ln 0,80 / l =19,96 ~20 heures. Selon vous, quels sont les moyens de protection utilisés autour d’une enceinte de radiothérapie ? Plaques de plomb.
Principe de l'expérience de Cavendish. J’ai pesé la Terre ! » aurait déclaré Cavendish en 1798. En effet, grâce à la mise au point d’une astucieuse balance de torsion (photo ci-dessous), il venait de mesurer les infimes forces de pesanteur qui agissent entre des masses ordinaires. Ceci lui permettait de déterminer la valeur de la constante universelle de gravitation G intervenant dans la loi de Newton énoncée en 1687. L’expérience de Cavendish a permis d’établir une valeur de référence pour la constante universelle de gravitation que nous noterons Gréférence. Cette valeur (6,67 x 10-11 N.m².kg-2) a permis le calcul de la masse de la Terre : M = 6 x 1024 kg. 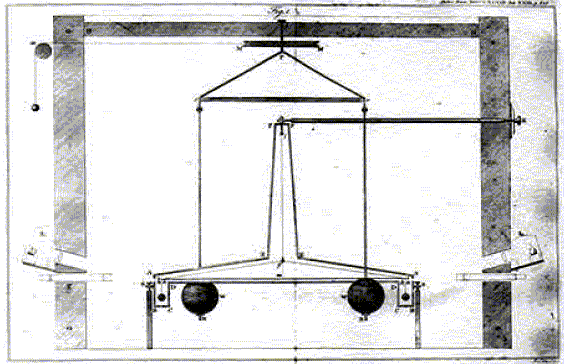 Le principe de la balance de torsion se fonde sur l’obtention d’un système qui établit l'équilibre entre le couple de torsion d'un fil et les forces d'attraction gravitationnelle. Elle est constituée de deux petites sphères de masse m, d’une tige de longueur a et d’un fil de torsion. De part et d’autre de la tige, on a placé deux autres sphères fixes de masse M en face de chacune des masses m (M très supérieure à m). L’ensemble est alors à l’équilibre (voir schémas ci-dessous). On écarte le pendule ainsi constitué de sa position d’équilibre. Celui-ci va alors osciller jusqu’à revenir dans son état d’équilibre initial. Une étude en laboratoire de la balance de Cavendish utilise toujours le même principe : deux petites masses m (15,0 g) aux extrémités d’une tige suspendue à un fil de torsion sont attirées par deux grandes masses M (1,50 kg). A l’équilibre, les forces de gravitation ont dévié le fléau de la balance d’un angle θ, angle qui peut être mesuré avec des capteurs diélectriques très sensibles, d’où une approche quantitative simplifiée et précise. 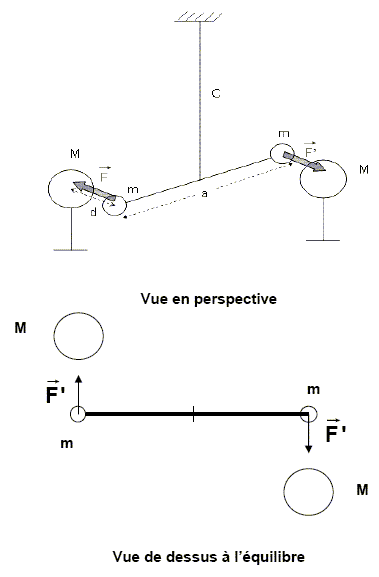 Le pendule est composé du fil de torsion, de la tige de longueur a et de masse négligeable aux extrémités de laquelle se trouvent deux petites sphères de masse m. Son moment d’inertie I est donné par la relation I =½ma2, a étant la distance entre les deux petites sphères de masse m avec a = 10,0 cm. Calculer la valeur numérique du moment d’inertie I en précisant son unité. m = 1,50 10-2 kg ; a = 0,100 m ; I = 0,5 *1,50 10-2 *0,1002 =7,50 10-5 kg m2. Le pendule oscille avec une période T de 702 s. On rappelle la relation entre la période T, le moment d’inertie I et la constante de torsion C du fil : T = 2π (I/C)½. Calculer la constante de torsion C du fil en précisant son unité. C =4p2I / T2 =4*3,142 *7,50 10-5 / 7022 =6,0082 10-9 ~6,01 10-9 kg m2 s-2 (N m). Que pourriez-vous prévoir concernant la valeur de la période si on venait à utiliser deux petites sphères plus légères ? C est une constante caractérisant le fil ; I est proportionnel à la masse m. Si la masse diminue, la période T diminue.
|
|||||||
|
|