Etude d'un thermomètre à diode : bac STL chimie de laboratoire 2011.

...

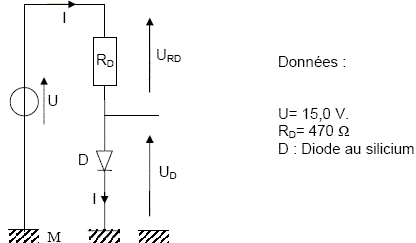
Cette partie est consacrée à l’étude d’un thermomètre qui donne la température en tête d’une colonne à distiller. Ce thermomètre est réalisé à partir d’une diode D au silicium comme l’indique le montage ci-dessous. 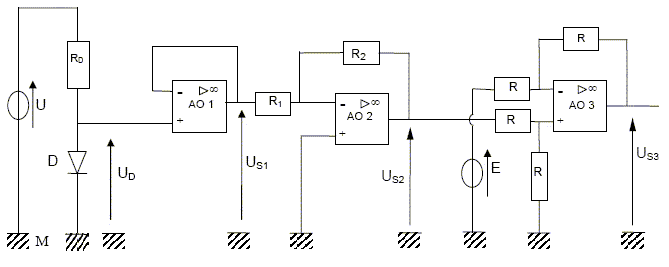Les amplificateurs opérationnels (A.O.) sont notés AO1, AO 2 et AO 3 sur les schémas. On considère ces amplificateurs comme parfaits et fonctionnant en mode linéaire. La courbe représentant l’intensité du courant I à travers la diode en fonction de la tension aux bornes de la diode est fournie. La tension UD dépend de valeur de la température q tel que : UD = - 2,03×10-3×q + 0,841 avec q en °C et UD en V. Etude du montage à diode à une température de 20°C. Écrire la loi des mailles dans le montage ci-dessus. U =UD + URD. Montrer que I = (U-UD)/RD. URD= RDI ; U =UD + RDI ;  I = (U-UD)/RD. Calculer I pour UD=0 V puis pour UD= 0,90 V. En déduire le tracé de la droite de charge dont l’expression est donnée. Tracer cette droite sur la courbe fournie. Pour UD=0 V : I = 15,0 / 470 =3,19 10-2 A. Pour UD=0,90 V : I = 14,1 / 470 =3,00 10-2 A. I = (15,0-UD) / 470 =3,19 10-2 - 2,13 10-3 UD. En déduire, graphiquement, la valeur de UD lorsque la diode est à 20,0 °C. 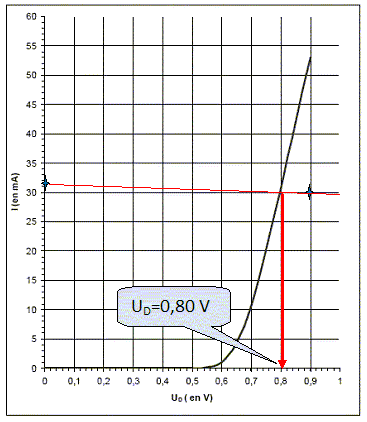Retrouver cette valeur à partir des données de l’énoncé. UD = - 2,03×10-3×q + 0,841 = - 2,03×10-3×20 + 0,841 = 0,800 V. Etude du montage autour de l’A.O. 1 : 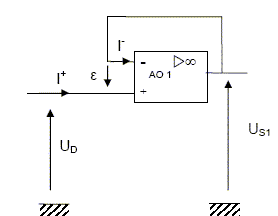Démontrer la relation entre US1 et UD. L'AO 1 est parfait et fonctionne en régime linéaire : e = 0. La tension est nulle aux bornes du petit fil reliant l'entrée inverseuse et la sortie de l'AO 1. UD = e +US1 ; UD =US1. Donner le nom de ce montage. Montage suiveur de tension. Préciser l’intérêt de ce montage. la tension de sortie est indépendante de la charge. Etude du montage autour de l’A.O. 2. Placer sur le schéma du montage  les tensions UR1 et UR2 aux bornes des résistances R1 et R2. 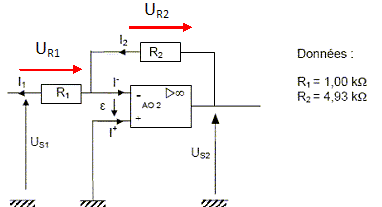 Rappeler les propriétés d’un amplificateur parfait en mode linéaire. e=0 et i+=i-=0. En utilisant les tensions UR1 et UR2, montrer l’expression de US2 = -(R2/ R1) x US1. UR1 = R1i1 ;  UR2 = R2 i2 ; US2 =UR2 ;  i1 = i2 car i- =0. D'où : i2 = US2 / R2 ;  UR1 +US1 = 0 soit : US1 = -R1 i1 = -R1 US2 / R2 ; US2 = -(R2/ R1) x US1. Déduire que l’expression de US2 en fonction de la température q est : US2 = 0,0100× q – 4,15 Avec q en °C et US2 en V. US2 = -(R2/ R1) x US1 = -(R2/ R1) x( - 2,03×10-3×q + 0,841) US2 = -4,93x( - 2,03×10-3×q + 0,841) US2 = 0,0100× q – 4,15. Etude du montage autour de l’A.O. 3. L’étude du montage montre que US3 = US2 - E A partir de cette relation, justifier que ce montage porte le nom de soustracteur. Ce montage effectue la différence entre la tension appliquée sur l'entrée non inverse de l'AO 3 et la tension appliquée sur l'entrée inverseuse de l'AO 3.  Exprimer US3 en fonction de q et de E. US3 = US2 - E =  0,0100× q – 4,15-E.  Déterminer la valeur de E pour que US3 soit proportionnelle à q. – 4,15-E =0 soit E = -4,15 V. Calculer US3 pour q = 20,0°C et q = 100°C. Préciser l’intérêt du montage. US3 = 0,0100× q  = 0,0100*20 =0,200 V à 20°C. US3 = 0,0100× q  = 0,0100*100 =1,00 V à 100°C. La température est proportionnelle à la tension. La température est égale à 100 fois la tension affichée.

menu