La tension
aux bornes d'une diode au silicium a la particularité de varier en
fonction de sa température. L'objectif de ce problème est d'étudier un
capteur de température utilisant cette propriété.
Relation entre la tension aux bornes de la diode et sa température.
On réalise le montage suivant :
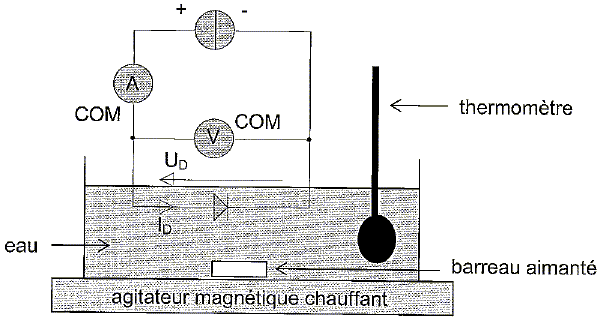
Le
générateur délivre un courant constant Id = 2,0
mA. Pour différentes température q
de l'eau, on mesure la tension Ud aux bornes de
la diode.
| q ( °C ) |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
| Ud
( V ) |
0,69 |
0,66 |
0,63 |
0,60 |
0,57 |
0,54 |
0,51 |
0,48 |
0,45 |
Tracer
Ud en
fonction de q.
Montrer
que la tension Ud obéit à
la relation Ud = a q + b.
Déterminer a et b en précisant les unités.
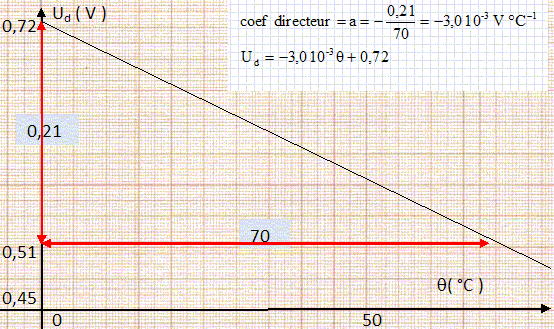
b = 0,72 V.
|
|
Etude
du capteur de température
: on insère la diode précédente dans le montage suivant.
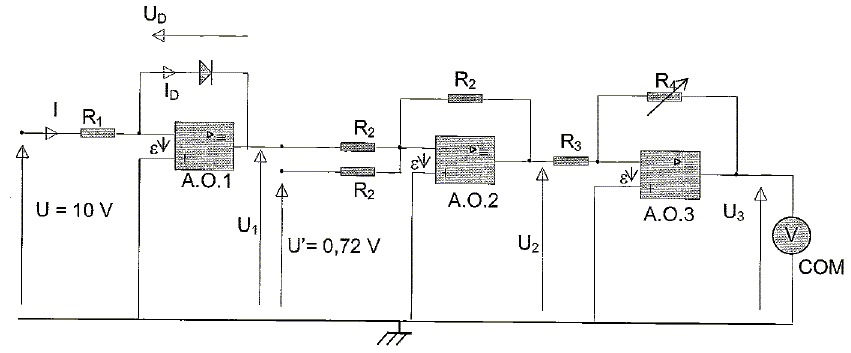
Les trois A.O sont supposés idéaux. R1
= R2 = R3 = 10 kW. R4
est un conducteur ohmique de résistance réglable.
Rappeler
les propriétés de l'A.O idéal en régime linéaire.
Les deux entrées sont au même potentiel : e = 0 V.
Les intensités des courants dans les deux entrées sont nulles : i+
= i- = 0.
Justifier
qu'ici les A.O peuvent avoir un fonctionnement linéaire.
Pour les trois A.O, il existe une liaison ( contre réaction ) entre
leur entrée inverseuse et leur sortie.
Montrer
que U1 = -Ud
= 3,0 10-3 q
-0,72.
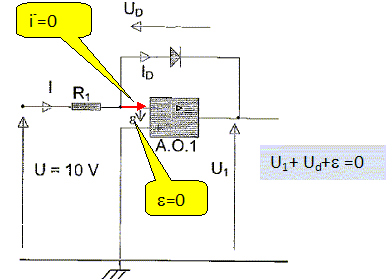
|
Les 3 résistances R2
étant identiques, le circuit autour de l'A.O 2 constitue un montage
sommateur inverseur : U2 = -(U1
+ U').
En déduire
l'expression de U2 en fonction de q.
U2
= -(3,0 10-3
q
-0,72 +0,72 )= -3,0 10-3 q .
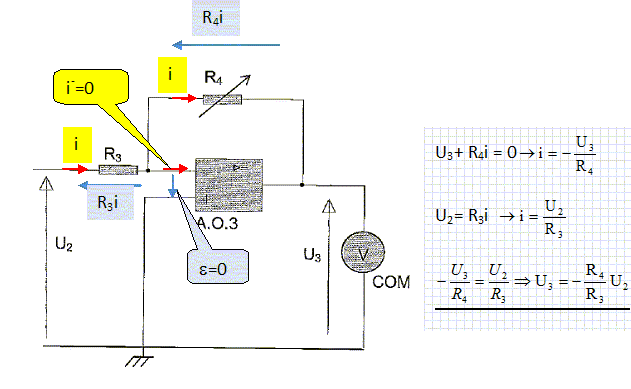
Montrer
que U3 = -R4 U2 / R3 et en
déduire l'expression de U3 en
fonction de R4 , R3 et q.
U3
= -R4 U2 / R3
= -R4
/ R3(-3,0 10-3 q ) = R4
/ R3 (3,0 10-3 q ).
Quelle
valeur faut-il donner à R4 pour que U3
= 10-3 q
?
U3
= R4
/ R3 (3,0 10-3
q ) = 10-3
q ; R4
=R3/ 3.
R3 = 10 kW. R4 = 3,3 kW.
|
|




