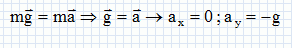|
Le
dauphin à flancs blancs du pacifique est peut être l'espèce la plus
abondante du Pacifique Nord. C'est un dauphin très sociable et qui
voyage généralement en groupe ; il est rapide puissant et bon surfeur.
Il est capable de délaisser un repas pour ettraper la vague provoquée
par le passage d'un navire. Un jour, un dauphin a fait un saut de trois
mètres pour se retrouver sur le pont d'un navire de recherche arrêter
en mer !
Quand il atteint sa taille adulte, il mesure environ 2,50 m et pèse
jusqu'à 180 kg.
Issu du site " Pêches et océans Canada ".
Etude
cinématique du saut du dauphin.
Dans cette partie on négligera l'action de l'air ( frottement et
poussée d'Archimède ) sur le dauphin. Au cours du saut, hors de l'eau,
le dauphin n'est soumis qu'à son poids.

|
On
souhaite étudier la trajectoire du centre d'inertie G du dauphin
pendant son saut hors de l'eau. le repère d'étude est ( O, i, j). On
choisit comme origine des dates l'instant où le centre d'inertie G du
daupphin est confondu avec le point O. Le vecteur vitesse initiale v0
est dans le plan (xOy ) et est incliné d'un angle a par rapport à l'axe Ox.
Grâce à l'exploitation d'un enregistrement vidéo du saut du dauphin, on
a pu trouver que la valeur de la vitesse est v0 = 10 m/s et
que a = 60°. On prendra g =
10 m s-2 et on note m la masse du dauphin.
|
En appliquant la
seconde loi de Newton, donner l'expression du vecteur accélération du
centre d'inertie du dauphin, puis ses coordonnées dans le repère d'étude.
Le dauphin
n'est soumis qu'à son poids.
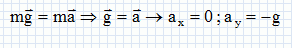
En
déduire l'expression littérale de la coordonée vx(t) du vecteur
vitesse, puis celle de la coordonnée vy(t).
Le vecteur vitesse est une primitive du vecteur accélération : vx(t)
= A, une constante déterminée par les conditions initiales.
vx(t)
= v0 cos a.
vy(t) = -gt + B avec B une constante
déterminée par la condition initiale.
vy(0) = B = v0
sin a.
vy(t) = -gt + v0
sin a.
Etablir
les équations horaires x(t) et y(t) du mouvement du centre d'inertie.
Le vecteur position est une primitive du vecteur vitesse. La position
initiale étant l'origine du repère, les constantes d'intégration seront
nulles.
x(t) = v0
cos a
t.
y(t) = -½gt2 + v0 sin a
t.
Il faut 0,87 s au dauphin pour atteindre le sommet S de la trajectoire.
Le saut
effectué est-il réellement d'au moins trois mètres de haut ? Justifier.
y(t=0,87) = -0,5 * 10 *0,872 + 10 sin 60 *0,87 = -3,7845
+7,5344 = 3,7 m.
Le saut réel est bien supérieur à 3 m de haut.
Les positions
du centre d'inertie du dauphin sont données à intervalles de temps
réguliers, l'echelle est 1 cm pour 0,50 m, la durée entre deux
positions est Dt = 0,10 s.
Déterminer
la valeur de la vitesse du centre d'inertie du dauphin aux points 4 et 6. On les notera v4 et v6.
v4 = (M3M4+M4M5)
/ (2Dt) ; M3M4+M4M5
mesure 2,5 cm soit en tenant compte de
l'échelle : 2,5*0,50 = 1,25 m.
v4 = 1,25 / 0,20 = 6,25 ~6,3 m/s.
v6
= (M5M6+M6M7) / (2Dt) ; M5M6+M6M7
mesure 2,0 cm soit en tenant compte de
l'échelle : 2,0*0,50 = 1,0 m.
v6 = 1,0 / 0,20 = 5,0 m/s.
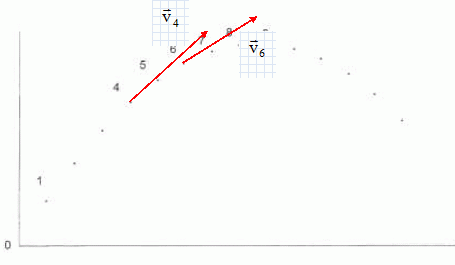
Tracer
les deux veteurs vitesses ( 1 cm
pour 2 m/s).
Le vecteur vitesse est porté par la tangente à la trajectoire au point
considéré et possède le sens du mouvement.
Construire
le vecteur 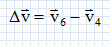 au point 5 et déterminer sa
valeur en utilisant l'échelle précédente. au point 5 et déterminer sa
valeur en utilisant l'échelle précédente.
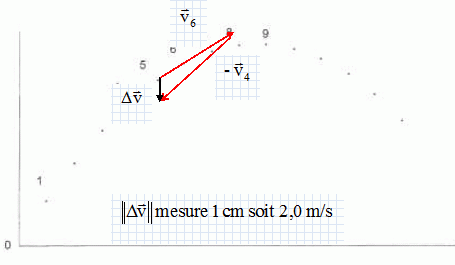
En
déduire la valeur a5 du vecteur accélération au point 5. Le
représenter. 1 cm pour 2 m s-2.
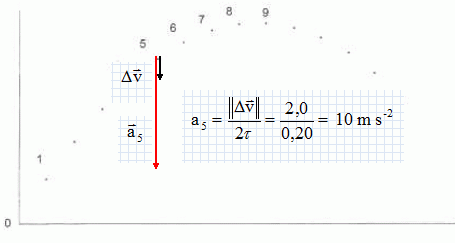
La valeur trouvée, la direction et le sens de l'accélération sont en
accord avec une chute libre ( actions de l'air négligées ).
|
|
.Etude
énergétique.
La position du centre
d'inertie G est donnée par ses coordonnées x et y, sa vitesse par ses
coordonnées vx et vy.
On donne la masse du dauphin m = 180 kg.
Exprimer l'énergie
cinétique Ec du dauphin en fonction de m, vx et vy.
Ec = ½mv2 = ½m(vx2 +vy2).
Exprimer l'énergie
potentielle de pesanteur Ep du dauphin en fonction de m, g
et y.
L'énergie potentielle de pesanteur est choisie nulle pour y=0.
Ep = m g y.
Montrer
que l'énergie mécanique du dauphin a pour valeur 9,0 kJ à la date t=0.
L'énergie mécanique est la somme de l'énergie potentielle et de
l'énergie cinétique.
E = Ec + Ep.
A la sdate t=0, l'énergie potentielle est nulle et la vitesse vaut v0
= 10 m/s.
E = ½mv02 = 0,5*180 *100 = 9,0 103 J =
9,0 kJ.
Par une étude énergétique, retrouver l'ordonnée yS du sommet
de la trajectoire.
Seul le poids travaille : l'énergie mécanique reste constante.
E = ½m(vx2
+vy2) +
m g y.
Au sommet S, la composante verticale de la vitesse est nulle :
E =½mv02
= ½m vx2 + m g yS =
½m (v0
cos a)2
+ m g yS.
½v02 =
½ (v0 cos a)2 + g yS.
yS = ½v02 (1-cos2 a)/ g = ½v02sin2 a / g.
yS =0,5 *100 *sin260 / 10 = 3,75 ~3,8 m.
|
|

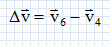 au point 5 et déterminer sa
valeur en utilisant l'échelle précédente.
au point 5 et déterminer sa
valeur en utilisant l'échelle précédente.