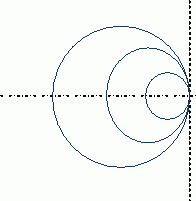Mesure de la vitesse du son ; ondes à la surface de l'eau : bac S.

. . . .

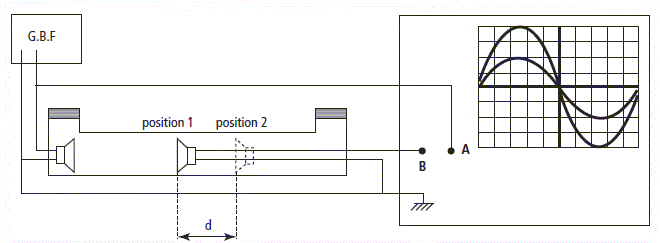Mesure de la vitesse du son dans différents gaz. d est la plus petite distance entre deux positions successives du microphone de droite pour lesquelles on observe les deux tensions en phase. Quelle est la tension visualisée sur la voie A ? Sur la voie A on visualise la tension délivrée par le GBF, c'est à dire la tension aux bornes du microphone situé  le plus à gauche. Sur la voie B, on visualise la tension aux bornes du microphone de droite. Quelle est la fréquence f de l'onde sonore ? On donne la base de temps de l'oscilloscope 100 µs / div. Une période correspond à 10 divisions soit T = 10*100 = 1000 µs = 1,0 10-3 s. f = 1/T = 1,0 103 Hz. Dans le diazote à 20°C, d = 34,9 cm. Calculer la célérité du son dans le diazote à cette température. d correspond à la longueur d'onde l ; or l = cN2 / f ; cN2= l f =0,349*1000 =349 ~3,5 102 m/s. Même question dans le dioxygène avec d = 32,6 cm à la même température. cO2= l f =0,326*1000 =326 ~3,3 102 m/s. Choisir, parmi les 4 hypothèses suivantes, laquelle est compatible avec les résultats trouvés ci-dessus. Hypothèse 1 :  la vitesse du son est proportionnelle  la masse molaire du gaz. cN2 / cO2=349 / 326 =1,070. MN2 / MO2=28 / 32 =0,875. cN2 / cO2 diffère de MN2 / MO2 : cette hypothèse est fausse. Hypothèse 2 : la vitesse du son est inversement proportionnelle  la masse molaire du gaz. 1/0,875 =1,14, valeur différente de 1,07 : cette hypothèse est fausse. Hypothèse 3 :  la vitesse du son est proportionnelle au carré de la masse molaire du gaz. 0,8752 =0,765, valeur différente de 1,07 : cette hypothèse est fausse. Hypothèse 4 : la vitesse du son est inversement proportionnelle à la raccine carrée de la masse molaire du gaz. (1/0,875)½ =1,07  : cette hypothèse est vraie. Calculer d en réalisant l'expérience dans le dihydrogène. MN2 / MH2=28 / 2 =14. 14½ =3,74 = cH2 / cN2 d'où cH2 =3,74 cN2 =3,74 *349 =1306 m/s. d = cH2 / f = 1306/1000 = 1,3 m. Ondes créées par un mobile en mouvement. Un mobile est animé d'un mouvement uniforme à la surface de l'eau. A0 est la position du mobile à la date t=0 ; A1 est la position du mobile à la date t1=5,0 s ; A2 est la position du mobile à la date t2=10,0 s .... Le cercle  centré sur A0 représente à la date t4 = 20,0 s, la position du front d'onde des perturbations créées. 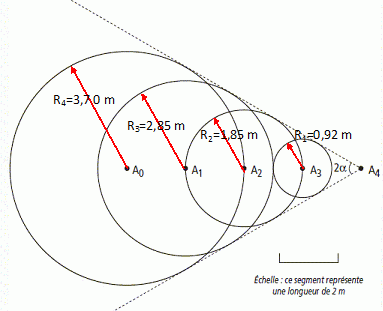Déterminer la vitesse V de propagation des ondes créées par le mobile à la surface de l'eau. V = R4/t4 = R3/t3 =R2/t2 =R1/t1 ~3,70 / 20,0 ~0,185 m/s. Déterminer la vitesse V' du mobile à la surface de l'eau. A0A1 / t1 = A1A2 / t1 =A2A3 / t1 =A3A4 / t1 =2,0 /5,0 = 0,40 m/s. Imaginons que le mobile soit un canard se déplaçant à la vitesse V', les perturbations créés par l'agitation de ses pattes se propagent à la vitesse V. Les deux segments de droites tracés en pointillés représentent le sillage du canard. Ils font entre eux un angle noté 2a. Exprimer la relation entre V, V' et a. sin a = 0,185 / 0,4 = 0,4625 ; a ~27°. Refaire le schéma dans le cas où V=V'. sin a = 1 ; a = 90° ; 2a = 180°. A partir de ce schéma expliquer pourquoi un avion ne peut pas se déplacer à une vitesse exactement égale à celle du son. ?  Les vibrations de l'air s'accumulent sur le nez de l'avion. Cette " superonde"  résultant de la somme des ondes émises produit une forte décompression : l'air fait donc défaut devant le nez et l'appareil doit accélérer pour dépasser le " mur du son ".

menu