Condensateur et éclairage d'un train miniature : bac S Nlle Calédonie 2010

. . . .

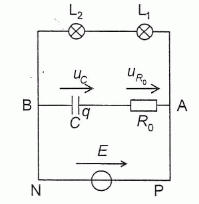
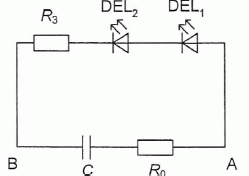
L'alimentation des trains miniatures se fait traditionnellement par des rails en 12 V continu. Utilisation de lampes à incandescence. Le dernier wagon du train comporte un circuit électrique relié aux deux roues arrière. Ce circuit est composé de : deux lampes à incandescence L1 et L2 qui sont les deux feux de fin du convoi, d'un condensateur de capacité C = 1000 µF, d'un conducteur ohmique de résistance R0 = 10 ohms, d'une alimentation de force électromotrice E = 12 V. Les figures suivantes  représentent les deux situations possibles d'éclairement des feux de fin de convoi. Les circuits électriques y sont représentés en gras. 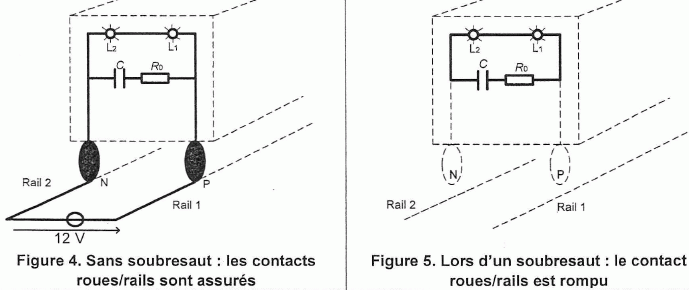Déplacement du train sans soubresaut. Le circuit électrique suivant représente les branchements du circuit de la figure 4. Répondre qualitativement aux deux questions suivantes :   Pendant la charge du condensateur, les lampes sont-elles parcourues par un courant ? La boucle contenant le générateur et les deux lampes est fermée ; la branche comportant le condensateur ne constitue pas un court-circuit : les deux lampes sont donc traversée par un courant. Lorsque le condensateur est totalement chargé, existe-t-il un courant dans la branche AB le contenant ? En courant continu, un condensateur complètement chargé, se comporte comme un interrupteur ouvert. Aucun courant ne traverse la branche AB contenant le condensateur. Déterminer la valeur de la tension aux bornes du condensateur lorsqu'il est complètement chargé. Justifier. On note u la tension aux bornes du condensateur chargé. Additivité des tensions : E = u + R0i avec i = 0. Par suite u = E = 12 V. Estimer l'ordre de grandeur du temps de charge du condensateur. La durée de la charge est de l'ordre de 5 fois la constante de temps du dipôle R0 C. 5 R0C = 5*10*1000 10-6 =  5 10-2 s. Déplacement du train avec soubresauts. 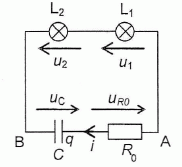En prenant de la vitesse, le train peut avoir des soubresauts et le contact trai/rails est alors rompu pendant une durée Dt de l'ordre du dixième de seconde. pendant le soubresaut le condensateur se décharge dans les lampes. Au début du soubresaut uC(t=0) = E = 12 V. les résistances des lampes indentiques valent R1 = R2 = R = 100 ohms. Dt = 0,10 s. Montrer que pendant le soubresaut, l'équation différentielle relative à la tension uC est de la forme : uC +(2R+R0)C duC/dt = 0. Additivité des tensions : uC+uR0+u1+u2 = 0. uR0= R0 i ; u1 = u2 =R i ; i = dq/dt avec q = CuC d'où i = C duC/dt. Par suite : uC +(2R+R0)C duC/dt = 0. (1) Vérifier que uC = A exp(-t / (2R+R0)) est solution de l'équation différentielle précédente et  déterminer la valeur de A. duC/dt = A (-1 / 2R+R0)C ) exp(-t / (2R+R0)), puis repport dans  (1) : A exp(-t / (2R+R0)) +(2R+R0)C A (-1 / (2R+R0)C ) exp(-t / (2R+R0)) = 0 A exp(-t / (2R+R0)) [ 1 -1] = 0 : égalité vérifiée quel que soit le temps. A t = 0, uC(t=0) = E =  12 = A e0 =A ; A = 12 V. L'expression de la puissance instantanée consommée par chaque lampe en fonction de l'intensité est donnée par la relation p(t) = R i2(t). On propose trois graphiques pouvant représenter l'allure de la puissance p(t) en fonction du temps, au cours de la décharge du condensateur. En utilisant l'expression de i(t) et en justifiant, choisir la seule figure pouvant représenter cette évolution. i(t) = CduC/dt = CE  (-1 / (2R+R0)C ) exp(-t / (2R+R0)) = -E / (2R+R0)C ) exp(-t / (2R+R0)) p(t) = R i2(t) =R  E2 / (2R+R0)C )2 exp (-2t / (2R+R0)). p(t) est une exponentielle décroissante. La figure 9 convient. 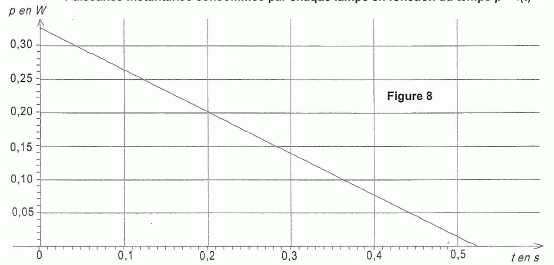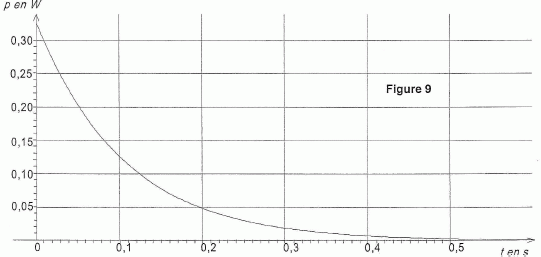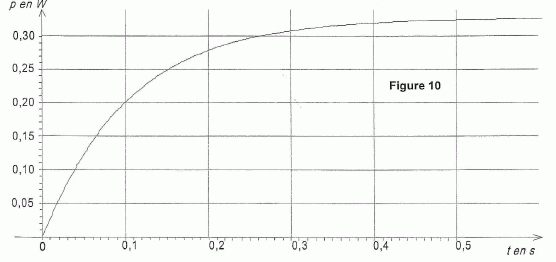L'éclairement de chaque lampe est optimal pour une puissance consommée P0 = 0,36 W. Toutefois, on considère que l'éclairement est satisfaisant si la puissance consommée est supérieure ou égale à 75 % de la valeur P0. Donner la durée d'éclairement satisfaisant pour chaque lampe. ( Détermination graphique ). 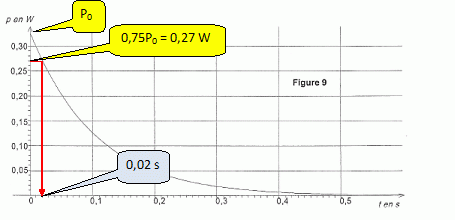Les lampes vont-elles éclairées de façon satisfaisante pendant toute la durée du soubresaut ? Le soubresaut dure 0,1 s, les lampes éclairent de manière satisfaisante durant 0,02 s : l'éclairement est très insuffisant. Utilisation de diodes électroluminescentes :  On peut remplacer les lampes L1 et L2 par des diodes électroluminescentes identiques notées DEL1 et DEL2 associées en série avec un conducteur ohmique de résisatnce R3. Elles ont une durée de vie plus longue et une consommation énergétique plus faible que les lampes à incandescence. Pendant un soubresaut, le schéma du circuit devient : Chaque diode émet de la lumière si elle est parcourue par un courant d'intensité supérieure à une intensité seuil Iseuil = 2,0 mA. Au début du soubresaut, à t=0, l'intensité est maximale et vaut Imax=6,0 mA. On donne R3 = 1,5 kW ; on admet que la durée d'éclairement des diodes est de l'ordre de  : Dt = (R3+R0) C ln( Imax / Iseuil)  Montrer par analyse dimensionnelle que Dt a bien la dimension d'un temps. ln( Imax / Iseuil) est sans dimension. Capacité C = charge / tension = intensité fois temps / tension ; (R3+R0) = tension /  intensité). (R3+R0) C a la dimension d'un temps. Calculer Dt et indiquer si les diodes vont éclairer pendant toute la durée du soubresaut. Dt = (R3+R0) C ln( Imax / Iseuil) = 1510*1000 10-6 ln(6 / 2) =1,66 ~1,7 s. Cette valeur est bien supérieure à la durée du soubresaut ( 0,10 s). Les diodes éclairent pendant toute la durée du soubresaut.

menu