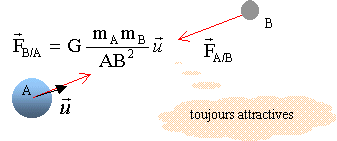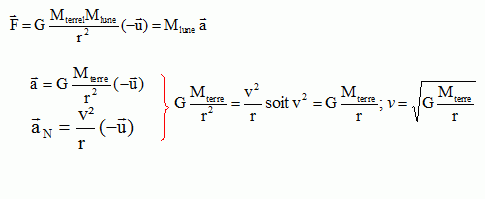Aurélie 03/02/11
 

 

Chute d'une balle de golf, mouvement circulaire uniforme, gravitation : bac S
. .
.
.

Balle de golf.

Les vecteurs sont écrits en bleu et en gras.

Soit une balle de golf : m= 45,9g ; D= 42,7 mm ; 384 alvéoles. Les alvéoles empêchent les couches d'air de se décoller de la surface de la balle lorsque la vitesse de celle-ci est importante. La balle est moins freinée que si elle était lisse.
Comme il est plus aisé de mesurer les vitesses pour des mouvements rectilignes, ils envisagent d'étudier, dans un premier temps, la chute libre d'une balle de golf dans le champ de pesanteur g supposé uniforme ( g=9,80 m/s²).
La balle est lâchée sans vitesse initiale en O, point pris comme origine de l'axe z orienté vers le bas,( vecteur unitaire n) donc de même sens que le champ de pesanteur g.
La résistance qu'oppose l'air au mouvement de la balle est supposée opposée au vecteur vitesse du centre de la balle et d'intensité proportionnelle au carré de la vitesse. La constante de proportionnalité est constante et notée k.
La poussée d'Archimède qu'exerce l'air sur la balle est négligeable.
Dans cette question on néglige la résistance de l'air afin de pouvoir procéder à une comparaison. La balle est soumise à son seul poids.
 Montrer que le mouvement du centre de la balle est rectiligne et trouver l'équation horaire z(t) du mouvement du centre de la balle. Quelle est la valeur de z pour v= 35 m/s ?
La balle est soumise uniquement à son poids ; la seconde loi de Newton s'écrit mg=ma.
La vitesse initiale est de plus nulle, en conséquence le mouvement est vertical vers le bas.
v(t) primitive de l'accélération : v(t) = gt
position, primitive de la vitesse : z(t) = ½gt².
éliminer le temps entre ces deux relations : v² = 2gz ou z = v² / (2g) = 35²/19,6 = 62,5 m.
  1. Dans la suite du problème, la résistance de l'air n'est pas négligée. On admet que le mouvement reste rectiligne, vertical du haut en bas. La seule composante non nul de la résistance de l'air est F= - kv²n avec v = dz/dt.
     Montrer que le principe fondamental de la dynamique donne : dv/dt + k/mv²=g (1).
La balle est soumise à son poids , vertical vers le bas et la résistance de l'air, verticale vers le haut ; la seconde loi de Newton s'écrit en projection sur l'axe z : mg- kv² =ma = mdv/dt.
g= k/m v²+dv/dt.
dv/dt = g( 1-k/(mg) v²) avec a² = k/(mg).
On écrira cette relation sous la forme dv/dt=g(1-a²v²) (2). Quelle est l'unité de 1/a ?

a² v² est sans dimension donc a est l'inverse d'une vitesse ou bien 1/a a la dimension d'une vitesse ms-1.

   

Expérimentalement on détermine la vitesse limite de chute vlim. Au dela le mouvement de la balle est rectiligne uniforme.
Vérifier qu'un mouvement rectiligne uniforme est solution de l'équation (2).
La vitesse limite étant atteinte, vlim = constante et sa dérivée dvlim/dt est nulle.
(2) s'écrit : 0 = g(1-a2vlim2) d'où : vlim = 1/a = (mg/k)½.
On mesure la vitesse limite vlim = 35 m/s. Que vaut k ?
calcul de k : k= mg/v2lim = 0,0459*9,8 / 352 = 3,67 10-4kg m-1.
 L''expérience montre qu'à t=10 s, la vitesse limite est atteinte. La distance que doit parcourir verticalement la balle pour atteindre la vitesse limite est alors 264 m.
Comparer le résultat précédent à la distance calculée à la première question.
264 m, valeur bien supérieure à 62,5 m calculée en 1. Il faut prendre en compte la résistance de l'air. Le modèle de la chute libre n'est pas correct.
Gravitation.
Constante de gravitation universelle G = 6,67 10-11 S.I. Le champ de pesanteur à la surface de la terre est g0 =9,8 N / kg et la masse de la terre est M = 6,0 1024 kg.
Le problème s'appuie sur le texte de R.P. Feynmann.
" Il est facile d'estimer de combien la lune tombe en une seconde, parce que vous connaissez la taille de son orbite, vous savez qu'il lui faut un mois pour tourner autour de la terre et si vous calculer combien elle parcourt en une seconde, vous pouvez calculer de combien l'orbite circulaire de la lune est tombée au dessous de la ligne droite qu'elle aurait empruntée, si elle n'avait pas pris le chemin qu'elle prend en fait.
Cette distance vaut un peu moins d'un millimètre et demi. La lune est soixante fois plus loin du centre de la terre que nous ; nous somme à 6400 km du centre et la lune est à 384 000 km. Donc si la loi du carré inverse est vraie, un objet à la surface de la terre devrait en une seconde tomber de 1,5 mm*3600 ( carré de 60) car d'ici à la lune la force s'affaiblit d'un facteur 60 x 60 par la loi du carré inverse. Or 1,5 mm x 3600 fait environ 5 mètres en une seconde ".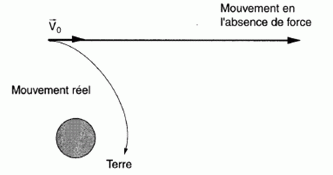
Ce texte met en évidence la nécessité d'exercer une force centripète pour créé un mouvement circulaire.
 Dans l'hypothèse de l'absence d'une force, quel serait le point A de la lune qui suivrait une trajectoire rectiligne ? Par rapport à quel référentiel ?
Dans un référentiel galiléen ( par exemple le référentiel héliocentrique ), un objet pseudo isolé ( soumis à aucune force ) est soit immobile, soit son centre de gravité est animé d'un mouvement rectiligne uniforme.
Quelle est la force responsable du mouvement réel de la lune ?
La force de gravitation attractive exercée par la terre sur la lune.
Quelle loi évoque l'auteur lorsqu'il fait allusion à la loi du carré inverse ? Donner l'expression de cette force.
L'interaction gravitationnelle (Newton ) entre les masses.
Deux corps A et B de masses respectives mA et mB séparés d'une distance d exercent l'un sur l'autre des forces opposées attractives, importantes dans l'infiniment grand, négligeables dans l'infiniment petit.

 

Dans l'hypothèse où l'on suppose le champ de pesanteur vertical et uniforme :
Exprimer sans démonstration la hauteur de chute h d'un corps lancé avec une vitesse horizontale v0 en fonction de g et de la durée de la chute t.
h = ½gt2.
Donner l'expression de la force de gravitation exercée par la terre sur un objet de masse m en un point situé à la distance r de son centre en fonction de G, M, m et r.
 On suppose que le point considéré est extérieur à la terre.
F = GMm / r2.
Expliquer pourquoi la valeur de h est divisée par 3600 lorsque l'on passe de la surface de la terre au point A lunaire ( pour une même durée t).
A la surface de la terre : F = GMm / R2  = mg0 avec g0 =GM / R2 .
Au point A : F = GMm / (60R)2  = mg avec g =GM / (60R)2  = g0 / 602.
h0 = ½g0t2 ; h = ½gt2 = ½ g0 / 602t2 =h0 / 602.
Retrouver la valeur de h ( 1,5 mm pour t = 1 s) en prenant r = 3,84 105 km.
g =GM / r2  =6,67 10-11 *6,0 1024 / (3,84 108 )2 =2,7 10-3 m s-2.
h = ½gt2= 0,5 * 2,7 10-3 *12 = 1,35 10-3 ~ 1,4 mm.



Le centre  d'inertie de la lune ayant une trajectoire circulaire.
Démontrer que son mouvement est uniforme.
La lune est soumise à la seule force de gravitation centripète exercée par la terre. Cette force est perpendiculaire à la vitesse du centre d'inertie G de la lune. En conséquence cette force ne travaille pas et ne modifie pas la valeur de la vitesse du centre d'inertie de la lune. Le mouvement de G est donc circulaire et uniforme.
Déterminer sa vitesse linéaire v en fonction de G, M et r.

Calculer v et retouver la période de rotation donnée dans le texte.
 v = (6,67 10-11 * 6,0 1024 / 3,84 108)½ =1,05 103 m/s.
La lune parcourt la circonférence 2*3,14 r à la vitesse v en T seconde.
T = 2*3,14 r / v = 2*3,14*3,84 108 / 1,05 103 =2,3 106 s
2,3 106 / (3600 *24) ~ 27 jours.





menu