Spectroscopie : suivi cinétique : bac S Liban 2011.

. . . .

Étude du fonctionnement d’un spectrophotomètre. Extrait d’une notice d’un spectrophotomètre : L’appareil comprend : - une source de lumière polychromatique (lampe) qui émet un faisceau de lumière en direction du monochromateur ; - un monochromateur (réseau + fente) : le réseau (système dispersif) décompose la lumière et dévie les rayons suivant leur longueur d’onde (apparition des radiations colorées de la lumière). La fente (système sélectif) permet d’isoler une radiation lumineuse de longueur d’onde donnée. Cette radiation est dirigée vers la cuve contenant la solution à analyser ; - une cuve (transparente aux radiations sélectionnées par le monochromateur) contenant la solution à étudier ; - un photocapteur : c’est un élément photosensible (en général une diode) qui transforme le signal lumineux en signal électrique ; - un calculateur : il traite le signal électrique pour calculer l’absorbance qui est proportionnelle à l’intensité du courant. Étude du réseau. Le réseau est un dispositif optique composé d’une série de fentes parallèles ou de rayures réfléchissantes. Dans les deux cas, les traits sont espacés d’une distance constante qu’on appelle le pas du réseau.  Étude d’une seule fente. On place perpendiculairement à la fente un faisceau de lumière monochromatique de longueur d’onde l. Le dispositif est schématisé ci- après : 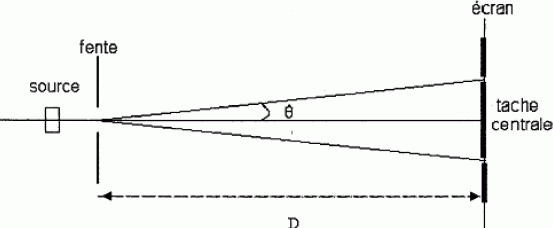On observe sur l’écran, situé à la distance D de la fente, la figure suivante : On donne D = 2,0 m ; largeur de la fente a = 100 µm. Quel phénomène observe-t-on lorsque la lumière traverse une fente de petite largeur ? On observe un phénomène de diffraction. La relation liant la longueur d’onde l, la largeur a de la fente et l’écart angulaire q est : q = l / a.  Préciser les unités de chaque grandeur. Ecart angulaire q en radian ; longueur d'onde l en mètre ;  largeur de la fente a en mètre.   Lorsque les angles sont petits, on peut admettre que tan q ~ q (q en radian). Établir dans ces conditions que L = 2 l D /a. tan q ~ q = ½L / D ; or q = l / a d'où : ½L / D = l / a soit L = 2 l D /a.  Déterminer la largeur de la tache centrale pour une radiation de longueur d’onde l1 égale à 500 nm. L =2*500 10-9 * 2,0 / 1,00 10-4 =0,020 m. On éclaire maintenant cette même fente avec une lumière blanche. En tenant compte du résultat de la question précédente et sachant que la largeur de la tache centrale est égale à 2,8 cm pour une radiation de longueur d’onde l2 égale à 700 nm, qu’observe-t-on sur l’écran ? La tache centrale de diffraction est blanche ( superposition de toutes les radiations de la lumière blanche ). De part et d'autre, on observe une alternance de taches sombres ( absence de lumière ) et de taches colorées. La radiation rouge est la plus déviée. Étude du réseau. Le phénomène précédemment étudié ci-dessus1 permet, entre autres, d’expliquer pourquoi le réseau décompose la lumière. Sachant que l’écart angulaire q augmente avec la longueur d’onde, quelle sera la couleur la plus déviée ? Les longueurs d'onde du rouge sont supérieures à celles du bleu : le rouge sera le plus dévié. 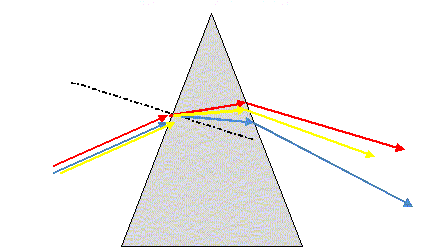Étude du prisme. Un prisme permet également de décomposer la lumière. Il est caractérisé par son indice de réfraction n. Définir un milieu dispersif. Dans un milieu dispersif, la célérité des ondes dépend de leurs fréquences. On souhaite étudier la déviation de rayons lumineux par un prisme de verre. Pour cela, on utilise deux radiations, l’une rouge de longueur d’onde lR = 750 nm, l’autre bleue de longueur d’onde lB = 460 nm. Les indices du verre pour ces deux radiations sont respectivement nR = 1,6 et nB = 1,7. L’indice de l’air nair est le même pour toutes les radiations. Les deux radiations arrivent sur la face d’entrée du prisme avec le même angle d’incidence i1. Pour laquelle de ces deux radiations, l’angle de réfraction dans le prisme est-il le plus grand ? On ne cherchera pas à déterminer la valeur des angles de réfraction. 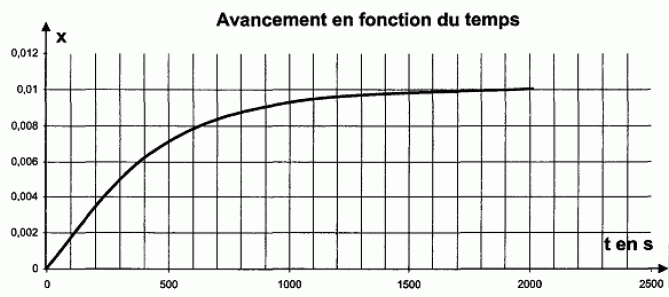n air sin i1 = nB sin iB ; sin iB = n air sin i1 / nB ; n air sin i1 = nR sin iR ; sin iR = n air sin i1 / nR ;  nB > nR  : donc sin iB > sin iR  : le bleu sera le plus dévié. Suivi cinétique par spectrophotométrie d’une transformation chimique. On étudie la transformation des ions iodure par les ions peroxodisulfate, modélisée par la réaction d’équation : S2O82-(aq) + 2 I-(aq) = 2 SO42-(aq) + I2(aq) Cette transformation est suivie à l’aide du spectrophotomètre précédemment étudié, relié à un système d’acquisition de données. Le protocole est le suivant : On introduit dans la cuve du spectrophotomètre un volume V0 = 1,0 mL de solution aqueuse d’iodure de potassium (K+(aq) + I-(aq)) de concentration molaire en soluté apporté C0 = 2,0 10-2 mol.L-1. À t = 0 s, on ajoute V1 = 1,0 mL de solution aqueuse de peroxodisulfate de potassium (2K+(aq) + S2O82-(aq) ) de concentration molaire en soluté apporté C1 = 2,0 10-1 mol.L-1. On mélange rapidement et on place la cuve dans le spectrophotomètre. Les mesures permettent de tracer la courbe ci-dessous donnant l’absorbance A du mélange en fonction du temps t. 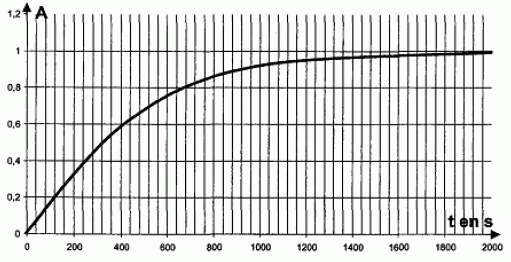Le tableau d’avancement de cette réaction est donné ci-dessous : état avancement (mol) S2O82-(aq) + 2 I-(aq)   = 2 SO42-(aq) + I2(aq) initial 0 C1V1 C0V0 0 0 en cours x C1V1 -x C0V0-2x 2x x fin xf = xmax C1V1 -xf C0V0-2xf 2xf xf Relation entre l’absorbance A et la concentration en diiode [I2] La loi reliant l’absorbance d’une solution et la concentration molaire de l’espèce colorée, ici le diiode, est donnée par la relation A = k.[l2(aq)] où k est une constante. Sachant que l’ion iodure est le réactif limitant et que la réaction est totale, déterminer la concentration du diiode dans le mélange à l’état final. C0V0-2xf = 0 ; xf =½C0V0 ; [I2] =½C0V0 / (V0+V1) =0,25 C0 =5,0 10-3 mol.L-1. Montrer que la valeur de la constante k est 2,0 102. Préciser son unité. L'absorbance finale est égale à 1  ( lecture graphe) : k = A / [l2(aq)] = 1 / 5,0 10-3 =2,0 102 L mol-1. Relation entre l’absorbance et l’avancement de la réaction x.  Montrer que x(t) = (V0+V1) A(t) / k. x(t) = [l2(aq)]  (V0+V1) et A = k.[l2(aq)] d'où : x(t) = (V0+V1) A(t) / k.  Faire le calcul numérique du coefficient (V0+V1)/ k. (V0+V1)/ k = 2,0 10-3 / 2,0 102 = 1,0 10-5 mol. Quelle est l’unité des valeurs numériques portées sur l’axe des ordonnées du graphe représenté ci-dessous ? xf = [l2(aq)]f  (V0+V1) = ½C0V0  = 1,0 10-5 mol = 0,01 mmol. On lit sur le graphe xf =0,01 mmol. Étude de la vitesse volumique de réaction. Définir la vitesse volumique de réaction vR. vR = 1/((V0+V1)) dx/dt.  En précisant la méthode utilisée, décrire l’évolution de la vitesse volumique de réaction au cours du temps. 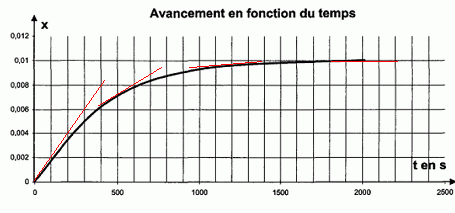[dx/dt]t : coefficient directeur de la tangente à la courbe à la date t. Les tangentes sont de moins en moins inclinées sur l'axe horizontal : [dx/dt]t diminue au cours du temps. VR est proportionnelle à [dx/dt]t : VR diminue donc au cours du temps. Quel facteur explique cette évolution ? La concentration des réactifs. Déterminer le temps de demi-réaction.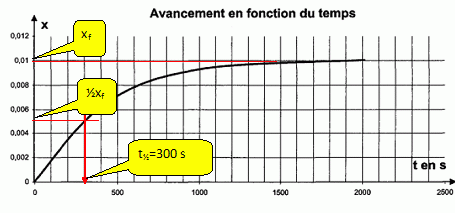

menu