Le pendule de Foucault : bac S France 09 / 2011.

. . . .

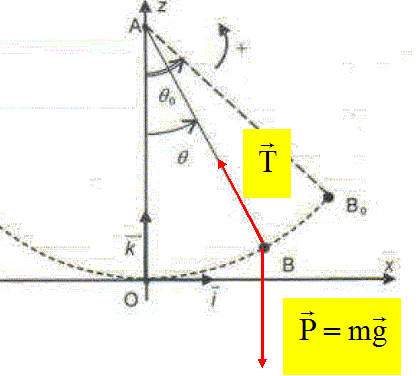
Dans tout l'exercice, les amplitudes angulaires qmax des oscillations sont inférieures à 10 °, soit 0,17 rad. On considère qu'on reste dans le cas des petites oscillations. La valeur du champ de pesanteur en un point de la surface de la terre dépend de la latitude l du lieu, elle ne dépend pas de sa longitude. gParis = 9,8 m s-2. T = 24 h, période de rotation de la terre dans le référentiel géocentrique. Période propre d'un pendule simple. On appelle pendule simple un système constitué d'un fil inextensible de longueur L, dont une extrémité est fixée à un support et l'autre attachée à un objet quasi ponctuel, de masse m. La masse du fil est négligeable par rapport à la masse de l'objet. Etude dynamique. Un pendule simple, constitué d'une petite sphère assimilée à un point B, de masse m = 50 g et d'un fil AB de longueur L = 2,0 m, est écarté de sa position d'équilibre d'un angle q0 inférieur à 10 ° puis lâché sans vitesse initiale. La position du point B peut être repérée par l'abscisse angulaire q = (AO, AB) ou par ses coordonnées (x, z).  Représenter sans souci d'échelle les forces qui s'exercent sur la sphère B pour un angle q quelconque. Les actions de l'air sont négligées. L'application de la deuxième loi de Newton dans le référentiel terrestre, considéré en première approximation comme galiléen, permet de montrer que le mouvement s'effectue bien dans le plan (xOz). 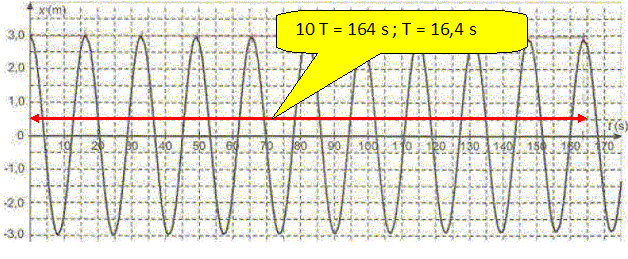Enoncer la deuxième loi de Newton sous forme d'une phrase. Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un solide est égale au produit de la masse M du solide par l'accélération de son centre d'inertie. Quels éléments permettent de ustifier l'affirmation que le mouvement est plan ? Les forces, poids et tension, sont situées dans le même plan (xOz) et la vitesse initiale est nulle. Dans l'approximation des petites oscillations, l'application de la deuxième loi de Newton permet d'établir l'expression de x(t). On donne trois possibilités pour x(t) dans lesquelles K est une constante positive. (a) x(t) = K sin (2pt/T0) ;  (b) x(t) = -K cos (2pt/T0) ;   (c) x(t) = K cos (2pt/T0) ; Le pendule est lâché sans vitesse initiale à t = 0 d'un angle correspondant à la figure ci-dessus, choisir l'expression qui vérifie les conditions initiales. A t = 0 q(t=0) = q0>0. x(t=0) ) =L sin q0 >0. (a) donne x(t=0) =0, elle ne convient donc pas. (b) donne x(t=0) =-K avec K >0, elle ne convient donc pas. (c) donne x(t=0) =+K avec K >0, elle  convient donc. 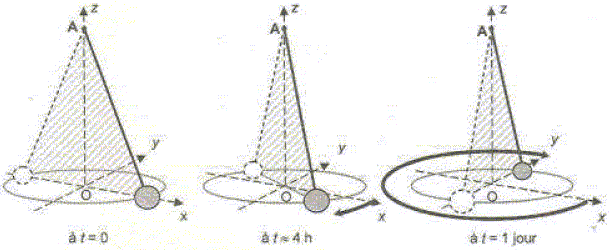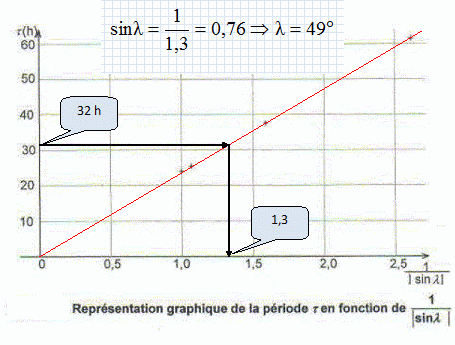Etude de la période. On montre que la période propre du pendule simple a pour expression T0 = 2 p (L/g)½.  Vérifier l'homogénéité de l'expression par analyse dimensionnelle. T0 est une durée : [T0]= T. 2 p  est sans dimension. [L/g] =L L-1 T2  =T2 ;  [(L/g)½] =T. A partir du XVIIIè siècle les horloges à balancier furent très utilisées pour mesurer le temps. On considère à Paris, une horloge dont le balancier a une longueur L = 1,0 m. Le balancier d'une telle horloge est un pendule aux oscillations entretenues et de faible amplitude que l'on peut modéliser par un pendule simple. Calculer la période propre du balancier de  cette horloge. T0 = 2 p (L/g)½ = 6,28 (1,0 /9,8)½ =2,0 s. Pourquoi dit-on que cette horloge "bat la seconde" ? La durée d'une demi-oscillation ( un aller ou un retour ) est égale  à 1,0 s. Que penser des indications données par cette horloge dans un lieu de latitude différente de celle de Paris ? L reste constante, par contre la valeur de g varie légèrement si la latitude du lieu change. L'horloge va donc avancer ou retarder.   Pendule de Foucault. Période du pendule. Le pendule de Foucault installé au Panthéon peut être assimilé à un pendule simple. On tracela courbe représentant l'abscisse x du centre B de la sphère en fonction du temps. Déterminer graphiquement la valeur de la pseudo-période T des oscillations à 0,1 s près. Retrouver la longueur du pendule de Foucault. (67 m). T2 = 4 p2 L/g ; L = T2 g / ( 4 p2 )=16,42 *9,8 /(4*3,142) =66,75 ~67 m. Quelle est l'origine de l'amortissement des oscillations ? L'action de l'air sur le pendule de Foucault est la cause de l'amortissement. Préciser la nature des conversions d'énergies mises en jeu lors des socillations du pendule. Lorsque l'amplitude angulaire est maximale, l'énergie mécanique du pendule est sous forme potentielle de pesanteur. Lorsue l'amplitude angulaire est nulle, l'énergie mécanique du pendule est sous forme cinétique. L'énergie potentielle de pesanteur est convertie en énergie cinétique lors du premier quart de période. L'énergie cinétique est convertie en énergie potentielle de pesanteur lors du second quart de période et ainsi de suite. Une partie de l'énergie mécanique est convertie en énergie thermique du fait des frottements. Comment évolue l'énergie mécanique du pendule au cours du temps ? L'énergie mécanique diminue du travail des frottements. Rotation du plan d'oscillation. Une observation pendant plusieurs heures montre que le plan d'oscillation tourne lentement, à vitesse constante, autour de l'axe vertical passant par le point de suspension A ; pour le pendule de Foucault, à Paris, en un jour, soit 24 heures, ce plan tourne de 270° dans le sens des aiguille d'une montre, comme l'illustre la figure ci-dessous. De nombreux pendules de Foucault ont été réalisés et placés en différents lieux sur la terre. L'étude de leur mouvement montre que la période, notée t, de rotation du plan d'oscillation dépend uniquement  de la latitude l du lieu. Pour un observateur fixe dans le référentiel terrestre, le mouvement du pendule n'est pas plan. Cette observation est en désaccord avec l'application de la seconde loi de Newton. Que peut-on en conclure quant au référentiel terrestre choisi pour faire l'étude ? Le référentiel choisi n'est pas galiléen. Calculer pour le pendule placé au Panthéon,la période de rotation du plan d'oscillation. Une période correspond à un tour complet soit 360 ° : t = 360/270*24 = 32 heures. Reporter le point correspondant sur le graphique. En déduire une méthode pour déterminer, à laide du pendule de Foucault, la latitude du lieu.

menu