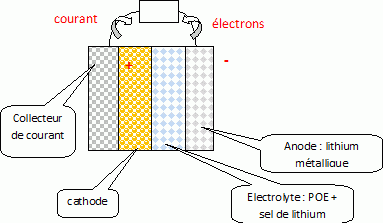
La bluecar : supercondensateur, panneaux solaires, batterie lithium métal polymère : bac S France 09 / 2011.

. . . .

Le supercondensateur. Les supercondensateurs ont une capacité de plusieurs milliers de farads et une tension d'utilisation de 2,7 V. Un supercondensateur est équivalent à un dipole associant en série un condensateur de grande capacité C et un conducteur ohmique de faible résistance R. 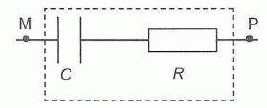Etude  théorique préalable de la décharge du supercondensateur. On étudie la décharge du supercondensateur, celui-ci ayant au préalable été chargé sous la tension d'utilisation E = 2,7 V. On donne le schéma du circuit de décharge. 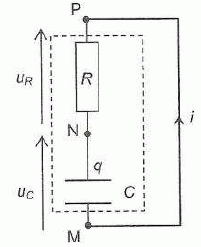 Exprimer la tension uR aux bornes du conducteur ohmique en fonction de sa résistance R et de i, puis en fonction de R, C et duc/dt. uR = Ri ; i = dq/dt avec q = Cuc d'où i = C duc/dt. Par suite uR =RCduc/dt. Etablir la relation entre uR et uc et en déduire l'équation différentielle vérifiée par uc. uR + uc = uPM ; or entre P et M il y a un simple petit fil de cuivre, donc uPM~0. uR + uc =0 ; RCduc/dt + uc =0 ; duc/dt +1/(RC) uc =0. (1) En vérifiant que l'expression uc(t) = E exp(-t / t) est solution de l'équation différentielle, montrer que l'expression de la constante de temps est t = RC. duc/dt = -E/t exp (-t / t) ; repport dans (1) : -E/t exp (-t / t) +1/(RC) Eexp (-t / t) =0 (1/(RC) -1/t) Eexp (-t / t) =0 Cette relation est vérifiée quel que soit le temps si t=RC. L'expression de l'intensité peut se mettre sous la forme i(t) = I0exp (-t / t). Montrer que l'intensité I0 à t=0 est égale à -E/R. Le condensateur est initialement chargé ; la continuité de l'énergie stockée par le condensateur conduit à : uc(t=0+) = E. De plus uR (t=0+)= R I(t=0+) et uc(t=0+) +uR (t=0+) =0 ; E +R I(t=0+) =0 ; I(t=0+) =I0 = -E/R. Etude de la variation de l'intensité du courant lors de la décharge du condensateur. On mesure avec un capteur de courant spécifique, l'intensité i du courant lors de la décharge du supercondensateur. On donne la courbe i(t) en fonction du temps. Le logiciel de traitement a permis de tracer la tangente à l'origine. Déterminer graphiquement I0; en déduire R et vérifier qu'elle est en accord avec l'indication du constructeur ( 0,35 mW ). 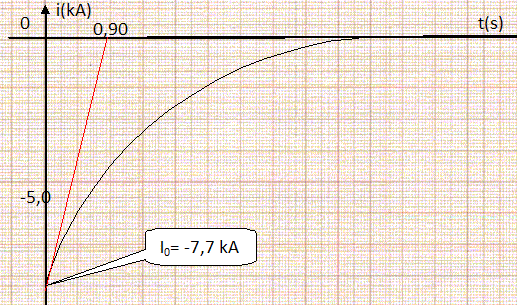R = -E/(I0) =-2,7 / (-7,7 103) =3,5 10-4 = 0,35 mW. ( Valeur en accord avec celle du constructeur) Déterminer graphiquement la valeur de la constante de temps t. L'intersection de la tangente à l'origine avec l'axe des temps donne la valeur de t ; t = 0,90 s. En déduire la capacité C. Est-elle en accord avec celle donnée par le constructeur ? ( 2,6 103 F).  C = t / R = 0,90 / 3,5 10-4 =2571 ~2,6 103 F. ( Valeur en accord avec celle du constructeur) Etude énergétique. Calculer la valeur de l'énergie électrique maximale Ec emmagasinée et restituée par le condensateur lors de sa décharge. Ec = ½CE2 =0,5 *2,6 103 *2,72 =9477 ~9,5 kJ. Comparer cette valeur de l'énergie avec les valeurs données : (masse du condensateur 0,500 kg ; énergie spécifique : 1,9 104 J kg-1 ). 1,9 104 *0,5 = 9500 J = 9,5 kJ ( valeur identique à celle du calcul précédent ). Les panneaux solaires. La cellule photovoltaïque est l'élément de base des panneaux solaires qui produisent de l'électricité. La lumière arrivant sur une cellule génère une tension à ces bornes. Lors de la conversion d'énergie lumineuse en énergie électrique, les atomes de silicium qui composent la cellule passent  d'un niveau d'énergie à un autre plus élevé. Ce "saut énergétique" peut se produire lorsqu'un photon est absorbé par le silicium. L'énergie minimale DE des photons nécessaire à la transition entre deux niveaux vaut 1,1 eV. h = 6,62 10-34 J s ; c = 3,00 108 m/s ; 1 eV = 1,60 10-19 J.  Calculer la longueur d'onde l dans le vide du rayonnement correspondant à cette transition. l = h c / DE = 6,62 10-34 * 3,00 108 / ( 1,1 *1,60 10-19) =1,128 10-6 m ~1,1 µm. Cette radiation appartient-elle au domaine visible ? Justifier. Le domaine visible s'étend de 0,40 µm à 0,80 µm. La radiation n'appartient pas au domaine visible, mais au domaine infrarouge 1,1 µm > 0,80 µm.   La batterie lithium métal polymère. La cellule électrochimique élémentaire de la batterie lithium métal polymère est basée sur l'utilisation de quatre composants : Cette cellule élémentaire est composée de deux électrodes au fonctionnement réversible. l'anode assure la fourniture des ions lithium lors de sa décharge et la cathode agit comme un réceptacle où  les ions lithium viennent s'intercaler. Les deux électrodes sont séparées par un électrolyte polymère solide, le polyoxyéthylène . la conduction est assurée par les ions obtenus lors de la dissolution de sels de lithium dans l'électrolyte. Le collecteur de courant est relié à la cathode pour assurer la connexion électrique. D'après le site internet http://www.batscap.fr. Caractéristiques de la batterie : énergie : 30 kWh ; tension nominale : 400 V ; puissance maximale : 45 kW ;quantité d'électricité maximale disponible 75 Ah. On donne : couple oxydant / réducteur Li+ / Li ; NA = 6,02 1023 mol-1 ; e = 1,60 10-19 C ; M(Li) = 6,9 g/mol ; 1 Ah = 3600 C. Représenter le sens conventionnel du courant électrique et le sens de circulation des porteurs de charge à l'extérieur de la batterie quand celle-ci débite. Quelle est la nature de la réaction se produisant au pôle négatif ? Quelle est la nature de la réaction se produisant au pôle positif ? Oxydation à l'anode négative ; réduction à la cathode positive. Ecrire la demi-équation d'oxydoréduction de la réaction se produisant au pôle négatif. Li(s) = Li+ +e-. Autonomie de la batterie. Calculer en coulomb la valeur de la quantité d'électricité maximale disponible qmax qui est donnée en Ah. qmax = 75 *3600 =2,7 105 C. En déduire la valeur de la quantité de matière d'électrons échangés n(e-) au cours de la réaction d'oxydoréduction en supposant que la batterie s'est complètement déchargée. n(e-) = qmax / (NA e) =2,7 105 / ( 6,02 1023*1,60 10-19) =2,803 ~2,8 mol. Calculer la masse de lithium correspondante. n(e-) = n(Li) =2,803 mol ; m = n(Li) M(Li) = 2,803 *6,9 =19,3 ~19 g. Calculer la valeur de l'intensité du courant Imax que peut débiter cette batterie. tension nominale : 400 V ; puissance maximale : 45 kW. Imax = puissance maximale / tension nominale = 45 103 / 400 =112,5 ~1,1 102 A. La batterie débite un courant d'intensité I = 100 A dans un circuit extérieur sous san tension nominale Unom. Calculer la durée maximale Dtmax de fonctionnement de la batterie. Dtmax  = qmax  / I =2,7 105 / 100 = 2,7 103 s ~0,75 heure. Etude de l'électrolyte. On donne la formule du polyoxyéthylène, aussi appelé polyéthylèneglycol. H(-O-CH2-CH2).....(-O-CH2-CH2)- OH. Nommer le groupe caractéristique écrit en gras. OH est le groupe hydroxy. A quelle famille de composés organiques appartient le polyoxyétylène ? Un polymère possédant une fonction alcool.

menu