Concert de violons : bac S France 2011.

. . . .

On donne la célérité du son dans l'air v = 340 m/s. 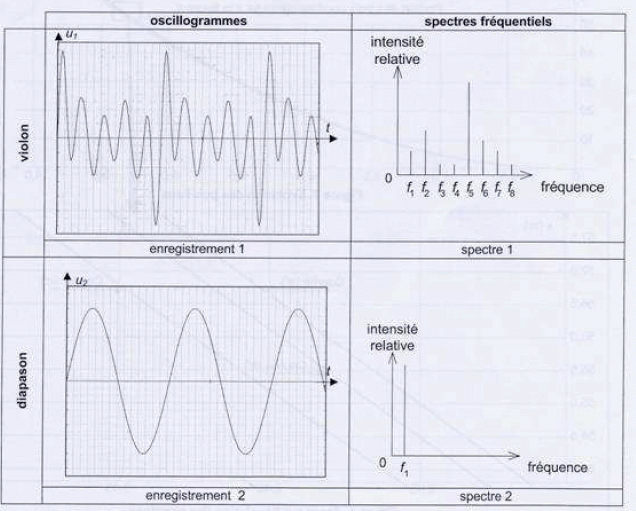Le violon. La figure ci-dessous représente les enregistrements réalisés dans les mêmes conditions, de sons de fréquences f1 = 440 Hz ( la3 ) émis par un violon d'une part et par un diapason d'autre part. Parmi les caractéristiques physiques d'un son musical figurent la hauteur et le timbre. Préciser la caratéristique qui différencie les sons des deux émetteurs. Le son émis par le diapason est pur : le spectre présente un seul pic, celui du fondamental de fréquence f1. Le son émis par le violon est complexe ( présence de plusieurs harmoniques dans le spectre). Le fondamental a la même fréquence f1. Les deux sons ont la même hauteur, mais des timbres différents. Quel nom donne-t-on à la fréquence f1 ? f1, la fréquence du fondamental donne la hauteur du son. Calculer les valeurs des fréquences f2 et f3 présentes dans le spectre fréquentiel du violon. f2 et f3 sont des multiples de f1. f2 = 2 f1 = 2*440 = 880 Hz. f3 = 3 f1 = 3*440 = 1,32 kHz. 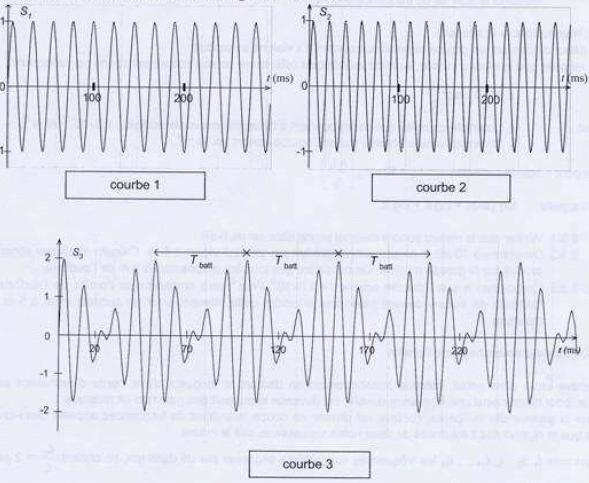L'ensemble des violons. Avant le concert, les violonistent cherchent à accorder leur instrument en jouant la note la3 de fréquence égale à 440 Hz. La fréquence émise par chaque instrument n'étant pas rigoureusement égale à 440 Hz, le son résultant est alternativement plus ou moins intense : on entend des battements qui sont des variations périodiques de l'amplitude sonore. Pour rendre compte de ce phénomène, on simule à l'aide d'un ordinateur des signaux dont les fréquences fa ( courbe 1) et fb (courbe 2) diffèrent légèrement : fa =420 Hz et fb = 460 Hz. On additionne ces deux signaux ( courbe 3). La période des variations d'amplitude, encore appelées battements, est notée Tbatt. On souhaite vérifier que fbatt = 1/ Tbatt = ½(fb-fa). 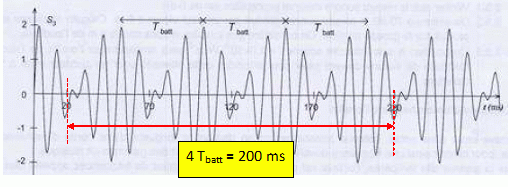Déterminer graphiquement fbatt et la comparer à ½(fb-fa). Tbatt = 0,050 s ; fbatt = 1/0,050 = 20 Hz. ½(fb-fa) =0,5(460-420) = 20 Hz. Lorsque le musicien constate l'arrêt des battements, que peut-il en conclure ? Les violons sont accordés : ils émettent tous un la3 à la fréquence de 440 Hz.. Comment accorder les violons ? On considère une corde de violon. On note L la distance entre les deux points de fixation sur l'instrument. Excitée dans son mode fondamental à la fréquence f0, la corde est le siège d'onde statonnaire, on observe un seul fuseau.. Donner la relation entre la longueur L et la longueur d'onde l. On observe des ondes stationnaires stables si 2L = nl avec n= 1 dans le cas d'un seul fuseau. Les ondes stationnaires résultent de la superposition d'ondes progressives de célérité v. Exprimer  v en fonction de f0 et L. l = v / f0 et l = 2L d'où : v = 2 L f0. On donne v = (F/µ)½ avec F valeur de la tension de la corde et µ sa masse linéïque. Vérifier l'homogénéité de cette équation. force = masse * accélération = masse * longueur / temps2. [F] = M L T-2. µ masse par unité de longueur ; [µ] = M L-1. [F / µ ] = L2 T-2.  [ (F/µ)½ ] = L T -1. (F/µ)½ est donc homogène à une vitesse. Donner une expression de f0 en fonction de F, µ et L. v = 2 L f0 = (F/µ)½  ; f0 =(F/µ)½  / (2L) = (F / (4L2µ))½. Si la corde d'un violon émet un son de fréquence 460 Hz, comment doit-on agir sur la corde pour retrouver la note la3 de fréquence 440 Hz ? La fréquence doit diminuer : L et µ étant constants, la valeur F de la tension de la corde doit décroître. La corde doit être détendue. Niveau sonore et intensité. Au début du concert, un groupe musical comportant dix violons se produit. On donne : L1 = 10 log (I/I0). I0 = 1,0 10-12 W m-2, intensité de référence correspondant à l'intensité minimale audible. Pour n sources : Ln = 10 log (nI/I0). Vérifier que le niveau sonore minimal perceptible est de 0 dB. Si I = I0 alors log (I/I0) = log 1 = 0 et L1 = 0. On estime à 70 dB le niveau sonore produit par un seul violon à 5 m. On considère que tous les violons sont à 5 m de l'auditeur. Calculer le niveau sonore produit par le groupe musical. I1 = I0 10 0,1 L1 = 10-12 107 = 10-5 W m-2 ;  n I1 = 10-4 W m-2 ; Ln = 10 log ( 10-4 / 10-12) = 10 log 108 = 80 dB. L'exposition à une intensité sonore I = 0,10 W m-2 peut endomager l'oreille de l'auditeur.  Combien de violons peuvent jouer pour atteindre cette intensité pour un auditeur situé à 5 m ? 0,1 / I1 = 0,1 / 10-5 = 1,0 104. Conduite d'un orchestre à l'oreille. L'octave entre deux notes, obtenue historiquement en divisant la longueur d'une corde d'instrument par deux, pour obtenir ainsi une fréquence double, est devenue le support des gammes en musique. Dans la gamme dite tempérée, l'octave est divisée en 12 intervalles de fréquences appelés demi-tons, tels que le rapport des fréquences de deux notes successives soit le même. Si on note f1, f2, f3 .... f13 les fréquences séparées par un demi-ton, on obtient f13/f1 = 2 par définition de l'octave. Vérifier que pour deux fréquences successives séparées par un demi-ton le rapport des deux fréquences est égal à 2 1/12. L'octave est divisée en 12 intervalles de fréquences ; le rapport des fréquences de deux notes successives est le même. 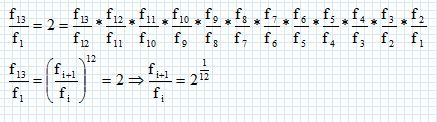Un chef d'orchestre possède les capacités auditives développées qui lui permettent de distinguer et reconnaître précisément et en particulier la note la3 et la note si3 située deux demi-tons au dessus. Calculer la fréquence de la note si3. fsi3 / fla3 = 22/12 = 21/6 ; fsi3 = fla3 * 21/6  = 440 *1,1225 = 494 Hz.

menu