Le laser mégajoule : bac S France 2011

Aurélie 23/06/11

Le laser mégajoule : bac S France 2011.

. .

.
.

Le laser mégajoule, qui sera l'un des plus gros laser au monde, est en construction sur le site du CESTA, près de Bordeaux.
Ce sera l'une des seules machines du genre capable de produire de l'énergie à partir de la réaction de fusion de l'hyudrogène.
Lorsqu'il sera opérationnel en 2014, ce gigantesque dispositif dimensionné pour accueilli 240 faisceaux lasers pourra délivrer une énergie de 1,8 mégajoule.
La chambre d'expérience, percée d'ouvertures pour laisser passer les faisceaux laser, aura un diamètre de 10 m. A l'intérieur, une bille de 2,4 mm de diamètre, remplie d'un mélange de deutérieum et de tritium solidifié de masse m = 300 µg sera fixée dans une cavité en or par des fils de soie d'araignée. Les faisceaux du LMJ convergerons alos sur cette cavité cible pour déclencher la réaction de fusion nucléaire. D'après les défis du CEA.
L'objectif de cet exercice est de comparer l'énergie fournie par le laser mégajoule à celle libérée par la réaction de fusion dans la cible.
On donne c = 2,998 10⁸ m/s ; h = 6,62 10^-34 Js ; 1 eV = 1,602 10^-19 J ; 1 u = 1,66054 10^-27 kg.

particule ou noyau
neutron
proton
deutérium
tritium
hélium 3
hélium 4

symbole
¹₀n
¹₁H ²₁H ³₁H ³₂He ⁴₂He

masse ( en u )
m_n=1,00866
m_p=1,00728 2,01355
3,01550
3,01493
4,00150

énergie de liaison ( MeV)

2,22
8,48

28,29

Lasers et énergie reçue par la cible.
Lee choix s'est porté sur des lasers à verre dopé au néodyme de longueur d'onde l₁ = 1050 nm.
Lorsque le faisceau laser entre dans la chambre d'expérience, un dispositif triple la fréquence de l'onde lumineuse.
En déduire la longueur d'onde l₂ du laser dans la chambre d'expérience.
l₁ = c / f₁ ; l₂ = c /(3f₁) = l₁ / 3 =1050 / 3 = 350 nm.

Dans quels domaines du spectre électromagnétique se situent les rayonnements de longueurs d'onde l₁ et l₂.
1050 nm ( supérieur à 800 nm ) appartient au domaine infrarouge ; 350 nm ( inférieur à 400 nm ) appartient au domaine ultraviolet.
Après le triplement de la fréquence, chaquuit une énergie E_laser = 7,5 kJ.
Par un calcul, montrer que la valeur de l'énergie E_LMJ délivrée au niveau de la cible par l'ensemble des faisceaux lasers composant le LMJ est en cohérence avec le texte introductif.

E_LMJ =240 E_laser =240*7,5 10³=1,8 10⁶ J = 1,8 MJ ( en accord avec le texte introductif ).
On admet que le LMJ est capable de délivrer l'énergie E_LMJen une durée Dt = 5,0 ns.
En déduire la puissance moyenne P_LMJ correspondante.
P_LMJ =E_LMJ / Dt = 1,8 10⁶ /5,0 10^-9 =3,6 10¹⁴ W.

Réaction de fusion deutérium tritium dans la cible.
On met en jeu deux isotopes de l'hydrogène, le deutérium et le tritium. Cette réaction de fusion produit un noyau, un neutron et de l'énergie.
Donner la composition des noyaux de tritium et de deutérium. Comment nomme t-on de tels noyaux ?
Deutérium ²₁H : 1 proton et 2-1 = 1 neutron ; tritium ³₁H : 1 proton et 3-1 = 2 neutrons.
Deutrium et tritium sont des isotopes.
Ecrire la réaction de fusion entre un noyau de deutérium et un noyau de tritium en précisant les lois utilisées.
³₁H + ²₁H---> ^A_ZX + ¹₀n.
Conservation de la charge : 1+1 = Z ; Z=2, on identifie l'élément hélium.
Conservation du nombre de nucléons : 3+2= A+1 d'où A = 4.
³₁H + ²₁H---> ⁴₂He + ¹₀n.
La courbe d'Aston ci-dessous représente l'opposée de l'énergie de liaison par nucléon en fonction du nombre de nucléons.

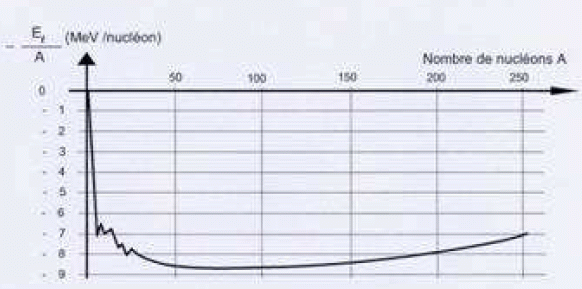
Dans quelle partie de cette courbe se trouve les noyaux susceptibles de fusionner ?
Les petits noyaux instables ( faible énegie de liaison par nucléon ) sont susceptibles de fusionner. Ils se trouvent dans la partie gauche de la courbe d'Aston. ( A < 20 ).
Donner la signification physique et l'expression de l'énergie de liaison E_l(^A_ZX) d'un noyau ^A_ZX d'un noyau de masse m(^A_ZX) en fonction de A, Z, m_p et m_net c.
On appelle énergie de liaison notée E_l d'un noyau l'énergie que doit fournir le milieu extérieur pour séparer ce noyau au repos en ses nucléons libres au repos.
E_l(^A_ZX) =[ Z m_p + (A-Z)m_n- m(^A_ZX) ] c².
Exprimer m(^A_ZX) en fonction de E_l(^A_ZX), A, Z, m_p et m_net c.
m(^A_ZX) =Z m_p + (A-Z)m_n - E_l(^A_ZX) / c².
En déduire les expressions des masses m(⁴₂He), m(²₁H) et m(³₁H).
m(⁴₂He) = 2 m_p + 2m_n - E_l(⁴₂He) / c².
m(²₁H) = m_p + m_n - E_l(²₁H) / c².
m(³₁H) = m_p + 2m_n - E_l(³₁H) / c².

Energie libérée lors de la réaction de fusion.
Exprimer l'énergie libérée |DE| lors de la réaction de fusion deutérium tritium en fonction des masses des noyaux et des particules mise en jeu.
|DE|=|m(⁴₂He) + m_n - m(²₁H) -m(³₁H)| c².
|DE|=|2 m_p + 2m_n - E_l(⁴₂He) / c² + m_n - (m_p + m_n - E_l(²₁H) / c²+ m_p + 2m_n - E_l(³₁H) / c²)| c².
|DE| = | E_l(²₁H) + E_l(³₁H)- E_l(⁴₂He) |
Calculer sa valeur en MeV.
|DE| =|-28,29 +8,48+2,22| =17,59 ~17,6 MeV.
Bilan énergétique dans la cible.
Sachant que le mélange est équimolaire, montrer que le nombre de noyaux N de deutérium ( ou de tritium ) présents dans la cible est N = 3,59 10¹⁹.
Masse de la cible m = 300 µg = 3,00 10^-7 kg.
m = N ( m(²₁H) + m(³₁H)).
N = m / (m(²₁H) + m(³₁H))
N = 3,00 10^-7 / ((2,01355+3,01550) *1,66054 10^-27) =3,59 10¹⁹.
En déduire l'énergie totale E_tot produite par la réaction de fusion dans la cible. La comparer à l'énergie E_LMJ fournie par le laser mégajoule.
E_tot= N |DE| = 3,59 10¹⁹ * 17,59 =6,319 10²⁰ MeV.
6,319 10²⁰ * 1,602 10^-13 = 1,01 10⁸ J = 101 MJ.
Cette valeur est environ 50 fois plus grande que l'énergie reçue par la cible.

menu