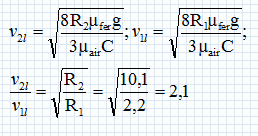Chute verticale d'un boulet : bac S France 2011.

. . . .

Galilée aurait étudié la chute des corps en lâchant divers objets du sommet de la tour de Pise. Dans cet exercice, on présente trois courts extraits de ces deux livres. " Dialogues sur les deux grands systèmes du monde " et "Discours concernant deux sciences nouvelles". Il s'agit de retrouver certains résultats énoncés par Galilée concernant la chute verticale dans l'air d'un boulet sphérique en fer, lâché sans vitese initiale. On donne g = 9,8 m s-2. Modèlisation par chute libre. Extrait n°1. Avant tout, il faut considérer que le mouvement des ciorps lourds n'est pas uniforme : partant du repos, ils accélèrent continuellement... Si on définit des  temps égaux quelconques, aussi nombreux qu'on veut, et si on suppose que dans le premier temps, le mobile partant du repos,  a parcouru tel espace, par exemple une aune ( 1,14 m) , pendant le second, il parcourera trois, puis cinq pendant le troisième ... et ainsi de suite, selon la suite des nombres impairs. Le boulet est lâché du point O, d'abscisse x0 = 0, à la date t0 =0. On supposera l'action de l'air négligeable. Dans ce cas,  l'équation horaire du mouvement du centre d'inertie G du boulet est : x(t) = ½gt2. Soient x1 la distance parcourue pendant la durée t, x2 la distance parcourue pendant la durée 2t et ainsi de suite. Exprimer x1, x2, x3 en fonction de g et t. x1 =½g t2 ; x2 =½g 4t2  = 2g t2 ;  x3 =½g 9t2  = 4,5g t2 . Exprimer la distance h1 =x1-x0 en fonction de g et t puis les différences h2 =x2-x1 et h3 =x3-x2 en fonction de h1. h1 =x1 =½g t2 ;   h2 =2g t2 -½g t2  =1,5 gt2  =3 h1. h3 =4,5g t2 -2g t2  =2,5 gt2  =5 h1. Retrouve t-on la suite des hauteurs de chute annoncée par Galilée ? Justifier. Durant des durées égales successives, les distances parcourues forment une progression arithmétique de raison 2 h1. h1 , 3 h1 ; 5 h1 .... (2n+1) h1 avec n entier. On retrouve la suite des hauteurs annoncées par Galilée. Etude de la durée de la chute. Les points de vue d'Aristote et de Galilée, au sujet de l'influence de la masse m du boulet sur la durée totale Dt de la chute diffèrent. Extrit n°2 : Cherchons à savoir combien de temps un boulet en fer met pour arriver sur la terre d'une hauteur de cent coudées (  une coudée = 0,57 m ). Aristote dit qu'une "boule de fer de cent livres tombant de cent coudées, touche terre avant qu'une boule d'une livre est parcouru une seule coudée", et je vous dis, moi, qu'elles arrivent en même temps. "Des expériences répétées montrent qu'un boulet de cent livres met cinq secondes pour descendre de cent coudées ". Une livre est une unité de masse. Parmi les propositions ci-dessous, attribuer celle qui correspond à la théorie d'Aristote et celle qui correspond à la théorie de Galilée. a) La durée de chute augmente quand la masse du boulet augmente. (ni Aristote, ni Galilée ) b) La durée de chute diminue quand la masse du boulet augmente ( Aristote ). c) La durée de chute est indépendante de la masse ( Galilée ). En utilisant l'expression x(t) = ½gt2, calculer la durée Dt de la chute d'un boulet qui tombe d'une hauteur H = 57 m ( 100 coudées). Ce résultat diffère de la valeur annoncée dans le texte. Justifier. H = ½gDt2 ; Dt = (2H/g)½ = (2*57 / 9,8)½ = 3,4 s. La chute réelle n'est pas libre, il faut prendre en compte les frottement du boulet sur les couches d'air. De plus Galilée ne connaissait pas le chronomètre, appareil de mesure très précis. Chute réelle. Galilée admet que les deux boules, de masses respectives une et cent livres, arrivent au sol avec un léger écart. Extrait n°3. Vous constatez, en faisant l'expérience, que la plus grande précède la plus petite de deux doigts, c'est à dire quand elle frappe le sol, celle-ci s'en trouve encore à deux doigts. Or derrière ces deux doigts, vous ne retrouverez pas les qutre-vingt dix neuf coudées d'Aristote. On considère que trois forces  s'exercent sur le boulet pendant la chute verticale : son poids P, la poussée d'Archimède F et la force de frottement f = ½pR2 µair Cv2. v : vitesse du centre d'inertie  du boulet ; R : rayon du boulet; C : une constante sans unité. On donne µair = 1,29 kg m-3 ; µfer = 7,87 103 kg m-3 ; volume d'une sphère : V = 4/3 pR3. Lors de la chute, représenter ces trois forces sur un schéma sans soucis d'échelle. 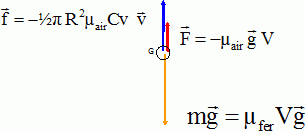Le poids et la poussée d'Archimède sont constants durant la chute. En déduire le rapport de leurs expressions et en déduire que la poussée est négligeable. mg / F =µfer / µair = 7,87 103 /1,29 = 6,10 103. La poussée est bien néglieable devant le poids. Appliquer la seconde loi de Newton sur l'axe Ox vertical, orienté vers le bas et déterminer l'expression  de la dérivée par rapport au temps  de la vitesse dv/dt. 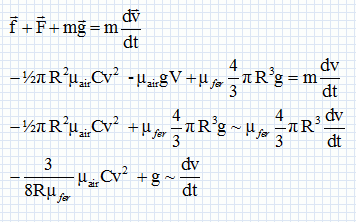Montrer que la vitesse limite vl est égale  à : 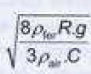. dvl / dt = 0 d'où : 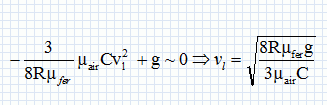Vérifier par analyse dimensionnelle que l'expression de vl est homogène à une vitesse. Le rapport µfer /µair est sans dimension ; C est sans unité. [g] = L T-2 ( accélération : mètre seconde-2 ) ; [R] = L ( longueur). [Rg] =L2 T-2  ; [(Rg)½] = LT-1 ; [vitesse ] = LT-1. On  considère deux boulets sphériques B1 et B2 en fer de masses respactives m1 = 1 livre et m2 = 100 livres et de rayons respectifs R1 = 2,2 cm et R2 = 10,1 cm. Donner l'expression du rapport v2l / v1l en fonction des seuls rayons et en déduire le boulet qui a la vitesse limite la plus élevée. Le boulet B2 possède la plus grande vitesse limite. Un logiciel permet de simuler les évolutions de la vitesse et de la position du boulet pendant la chute. Ces courbes sont obtenues pour les trois situations suivantes : - Chute du boulet B1 dans l'air ( courbes c et c') - Chute du boulet B2 dans l'air ( courbes b et b') - chute libre ( courbes a et a' ). 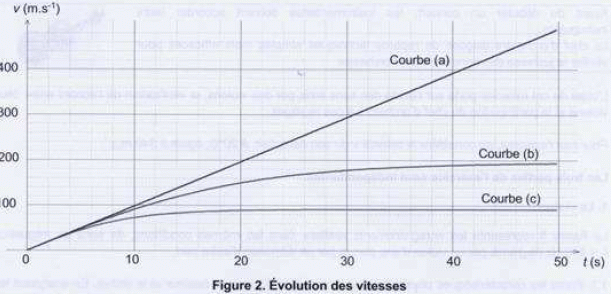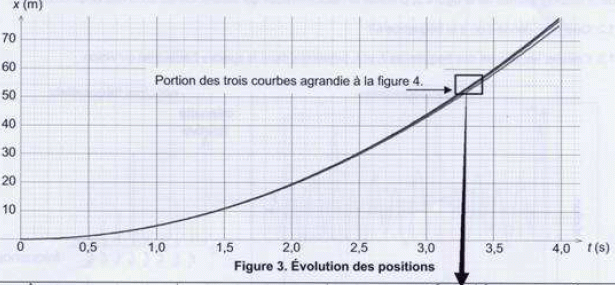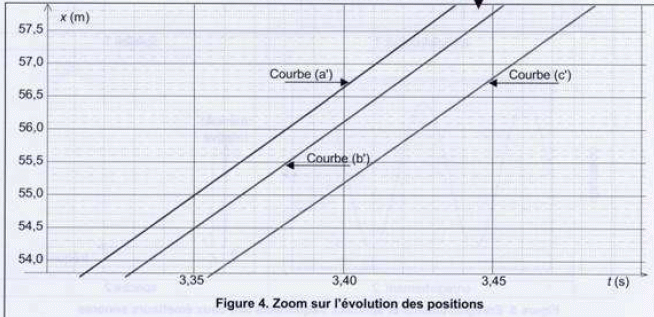Expliquer l'attribution des courbes b et c aux bouelts B1 et B2. Excepté durant les premières secondes de chute, les vitesses réelles sont inférieures à la vitesse d'une chute libre. Les mouvements réels conduisent à une vitesse limite constante. Le boulet B2 possède la plus grande vitesse limite. La hauteur de chute est de 57 m. Déterminer graphiquement la date tsol à laquelle le premier boulet touche le sol. S'agit-il de B1 ou de B2 ? 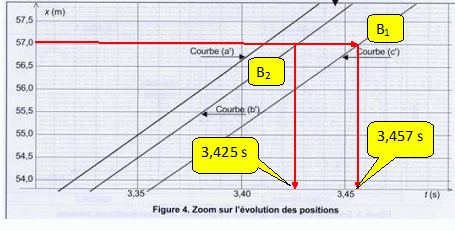A quelle distance du sol se trouve l'autre boulet à cette date ? Ce résultat est-il en accord avec l'extrait n°3 ? 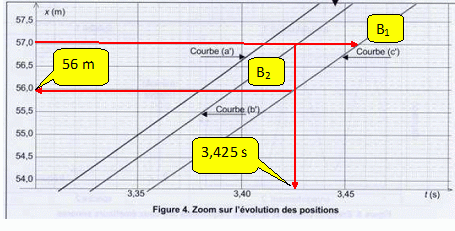La différence est de 1 m : cela n'a rien à voir avec les "deux doigts" de l'extrait.

menu