Tony est passionné par la guitare électrique. Afin de jouer les
morceaux de musique de ses idoles des années 70, il voudrait modifier
le son de sa guitare en utilisant une pédale d’effet wha-wha, qu’il
souhaite construire lui-même. Après quelques recherches sur internet,
il trouve le schéma électrique et les composants dont il aura besoin
pour réaliser sa wha-wha. Parmi ces composants se trouventplusieurs condensateurs et une bobine d’inductance L = 0,50 H.
De nombreux forums de guitaristes conseillent de fabriquer soi-même la bobine dont on a besoin.
Tony
a récupéré un noyau de ferrite, il enroule sur ce support du fil de
cuivre isolé pour obtenir la bobine. A présent, il souhaite déterminer
la valeur de l’inductance de la bobine ainsi constituée. Aussi va-t-il
s’aider de ses cours de physique…
Méthode 1.
Tony
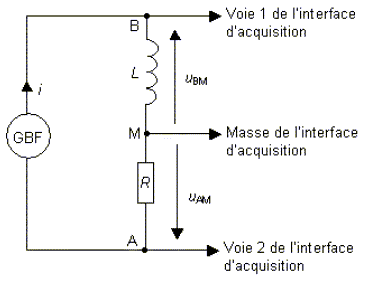
réalise le montage, représenté, comportant un générateur de basses
fréquences délivrant une tension périodique triangulaire de fréquence
f, un conducteur ohmique de résistance R = 10 kW
et la bobine d’inductance L dont on négligera la résistance interne. A
l’aide d’une interface d’acquisition reliée à un ordinateur, il
enregistre l’évolution en fonction du temps des tensions uAM (t) et uBM (t).
Les courbes représentent les évolutions de l’intensité du courant i (t) et de la tension uBM (t) en fonction du temps.
|
Déterminer la période de la tension délivrée par le GBF. En déduire sa fréquence.
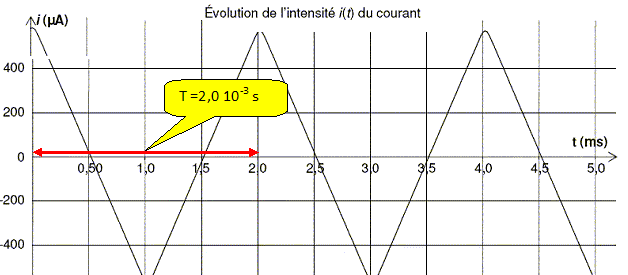
Fréquence f = 1 / T = 1 / 2,0 10-3 = 5,0 102 Hz.
.
|
Donnée : uAM (t) = − R.i(t)
Quel
traitement mathématique faut-il demander au logiciel d'effectuer pour
obtenir la courbe d’évolution de l’intensité du courant en fonction du
temps ?
Diviser uAM(t) par -R ( -104 ) pour obtenir l'intensité en ampère ; ou multiplier uAM(t) par -100 pour obtenir l'intensité en µA.
Expliquer pourquoi on peut écrire i (t) = a.t + b pendant des intervalles égaux à une demi-période.
Sur
chaque demi-période, la courbe est un segment de droite. L'équation
d'un segment de droite est celle d'une fonction affine par intervalle,
soit i(t) = at+b ( a et b constants ).
Tony utilise les fonctionnalités de modélisation du logiciel.
Données : Pendant l’intervalle de temps [3,0 ms ; 4,0 ms], il trouve que i(t) = 1,19× t – 0,0042 (avec i en A et t en s) et uBM (t) = 0,26 V.
On rappelle que la résistance interne de la bobine est négligeable.
Donner l’expression littérale de uBM (t) en fonction de L et de di/dt.
uBM(t) = L di/dt.
À
partir des résultats de la modélisation, calculer di/dt dans
l’intervalle de temps [3,0 ms ; 4,0 ms] puis déterminer la valeur de
l’inductance L.
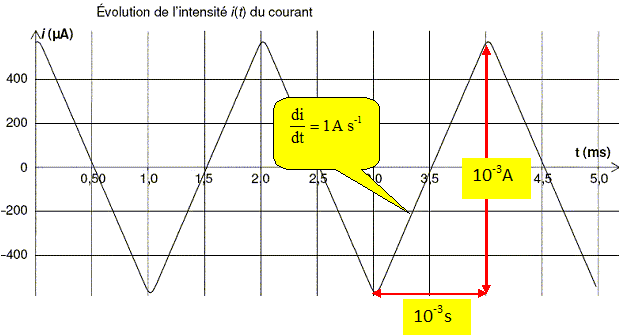
L = uBM(t) /( di/dt) = 0,26 / 1 = 0,26 H.
N’ayant
pas obtenu la valeur d’inductance désirée pour réaliser sa pédale
wha-wha, Tony poursuit la confection de sa bobine et teste l’inductance
par une seconde méthode.
Seconde méthode.
Tony
souhaite réaliser un montage lui permettant de décharger un
condensateur dans sa bobine. Il schématise le circuit suivant qu’il va
utiliser par la suite.
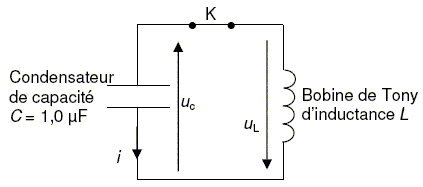
Tony
se souvient que la tension uc(t) aux bornes du condensateur oscille au
cours du temps. Si la résistance totale du circuit est négligeable,
l’équation différentielle qui régit l’évolution de la tension uc(t) est
:
d2uc/dt2 + 1/(LC) uc =0 (Équation (1))
Établir cette équation différentielle (1) en précisant la loi utilisée.pondant.
Additivité des tensions dans le circuit série.
uc +uL=0 ; uL=L di/dt ; i = dq/dt = Cduc/dt ; di/dt = Cd2uc/dt2 ;
uL=LCd2uc/dt2 ; uc +LCd2uc/dt2 =0 ; d2uc/dt2 + 1/(LC) uc =0.
On rappelle que l’expression de la période propre T0 des oscillations est : T0 = 2p(LC)½ .
Après
avoir chargé le condensateur, Tony l'introduit dans le circuit puis à
l'instant de date t = 0 s, il ferme l'interrupteur K. Il enregistre
alors l'évolution en fonction du temps de la tension uC(t)
aux bornes du condensateur. La courbe obtenue est représentée. Il se
rend alors compte qu’en réalité la résistance totale du circuit n’est
pas négligeable.
Nommer le régime des oscillations.
Lamplitude des oscillations diminue au cours du temps : régime pseudo-périodique.
À
partir de la courbe, déterminer précisément la valeur du temps
caractéristique T de ces oscillations en expliquant votre méthode.
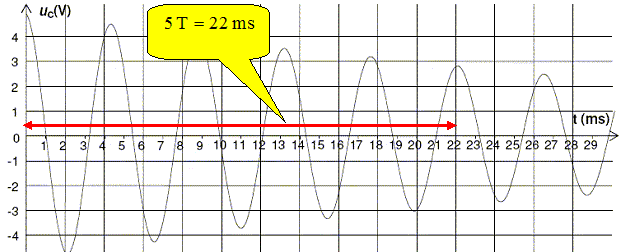
T = 22 / 5 = 4,4 ms = 4,4 10-3 s.
En déduire la valeur de l’inductance L de la bobine fabriquée par Tony.
L = T2/(4p2C) =(4,4 10-3)2/(4*3,142 *1,0 10-6) =0,49 H.
|
|
Étude énergétique.
Tony
souhaite réaliser l’étude énergétique de son circuit. Il utilise les
fonctionnalités de son tableur afin de calculer l’énergie électrique Eél stockée par le condensateur et l’énergie magnétique Em emmagasinée par la bobine. Les courbes d’évolution de ces énergies en fonction du temps sont données ci-dessous.
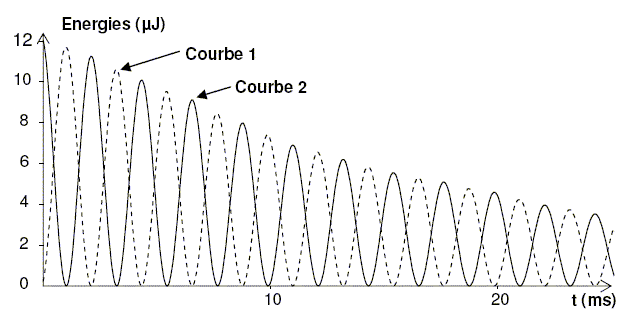
Par un raisonnement physique simple, identifier les courbes 1 et 2 représentées.
Initialement le condensateur chargé au maximum stocke toute l'énergie du dipole (RLC) : courbe 2.
Initialement l'intensité est nulle et la bobine ne stocke pas d'énergie : courbe 1.
Quel est le phénomène à l’origine de la diminution de l’énergie stockée dans le circuit ?
Lors
des échanges d'énergie entre bobine et condensateur, une partie de
celle-ci se dissipe sous forme d'effet Joule dans les parties
résistives du dipole.
|





