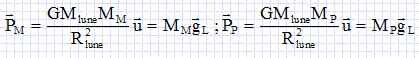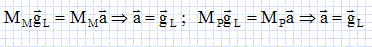Le
21 juillet 1969, Neil Armstrong fut le premier homme à poser le pied
sur la lune. Davs Scott réalisa une expérience de physique : il prit
dans ces mains levées à hauteur des épaules, un marteau dans l'une et
une plume dans l'autre. Puis il les lâcha en même temps. La plume tomba
comme le marteau. Dans l'exercice, l'indice M sera attribué au marteau
et P à la plume.
Faire le bilan des forces qui s'exercent sur la plume et sur le marteau à l'instant où ils sont lâchés.
Le marteau et la plume sont soumis à une seule force, la force de
gravitation due à la lune, ou poids du marteau et de la plume à la
surface de la lune.
Sur la lune, il n'y a pas d'atmosphère, donc pas de force de frottement due à l'air.
Donner l'expression de ses forces.
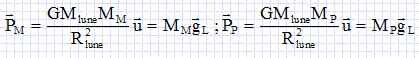
|
|
En appliquant la seconde loi de Newton, montrer que ces deux ojets ont le même vecteur accélération que l'on précisera.
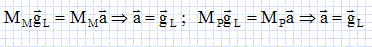
A
l'instant du lâcher, pris commeorigine des temps, le centre d'inertie G
du marteau est à h = 1,50 m du sol. Le mouvement est étudié dans le
référentiel lunaire, muni d'un repère, l'axe Ox correspond au sol.

Des graphiques 1 et 2 ci-après, lequel correspond à la trajectoire de G ?
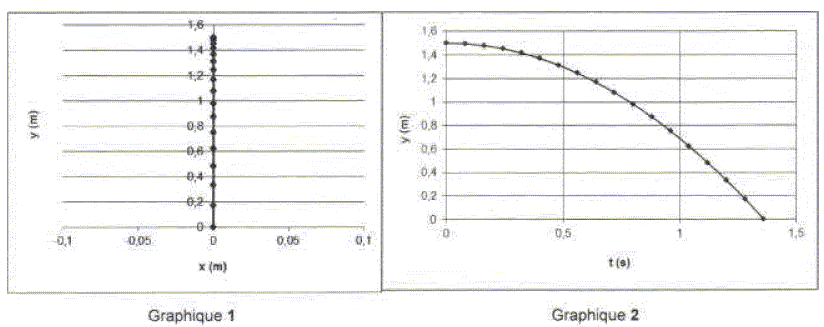
Le graphique 1 convient : chute verticale sans vitesse initiale. La trajectoire est une droite ; le mouvement est accéléré.
Le graphique 2 ne représente pas la trajectoire mais la hauteur de chute en fonction du temps.
|
Quelles sont les coordonnées du vecteur acclération dans le repère choisi ?
ax = 0 ; ay = -gL.
Quelles sont les coordonnées du vecteur vitesse de G ?
Le
vecteur vitesse est une primitive du vecteur accélération. La vitesse
initiale étant nulle, les constantes d'intégration seront nulles.
vx = 0 ; vy = -gL t.
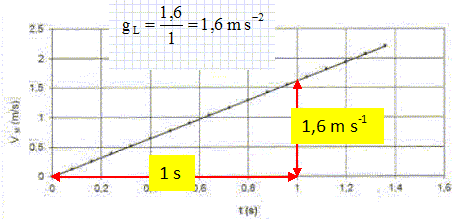
En déduire l'expression en fonction du temps de la norme, notée vM du vecteur vitesse de G. En quoi le graphique ci-dessous est-il compatible avec cette expression ?
vM = (vx2 + vy2)½ = gL t.
Le
graphique ci-dessous est une droite passant par l'origine ; son
équation est du même type, y = ax, que l'expression de la vitesse. Le
coefficient directeur de cette droite donne gL.
Durée de la chute.
Etablir l'équation horaire du mouvement y(t).
Le vecteur position est une primitive du vecteur vitesse. Les coordonées de la position initiale sont (0 ; h = 1,50 m)
x=0 ; y = -½gLt2+h = -0,80 t2 +1,50.
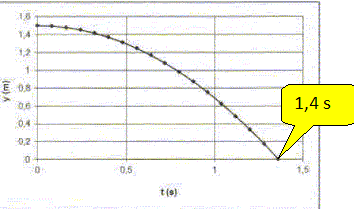
En déduire la durée de la chute et la vérifier graphiquement.
-0,80 t2 +1,50 = 0 ; t = (1,50 / 0,80)½ =1,37 ~1,4 s.
On serait arrivé à la même réponse à partir de la plume. " La plume tomba
comme le marteau".
Marchons sur la lune.
Pendant
la marche, on peut considérer que lors de l'impulsion du pied sur le
sol, le centre de gravité G du corps ( situé un peu au dessous du
nombril ) est projeté vers le haut et retombe à sa position de départ
quand l'autre pied prend contact avec le sol, un pas ayant été alors
accompli. Le mouvement de G peut-être assimilé, pour simplifier, au
mouvement du centre de gravité d'un objet lancé vers le haut avec la
vitesse initiale v. G décrit ainsi une trajectoire correspondant au
graphique suivant :
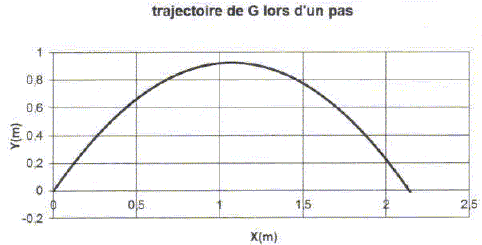
Valeur de la vitesse initiale v = 2,0 m/s ; elle fait avec l'horizontale l'angle a = 60°.
On se propose de calculer la longueur du bond correspondant à un pas.
L'étude théorique du mouvement de G conduit aux équations horaires :
x = v cos a t ; y = -½gL t2 + v sin a t.
L'instant t=0 est pris au début du pas.
Démontrer en établissant la fonction y(x) que la trajectoire de G est une portion de parabole.
t = x /( v cos a ) ; repport dans y(t) : y = -½gL x2 /( v cos a )2 + tan a x.
Expression de la forme y = A x2 + B x avec A et B constants ; il s'agit de l'équation d'une parabole.
Quelles sont les valeurs de y au début et à la fin du pas dans le repère choisi ?
y(t=0 ) = 0 ; y( t = fin du pas) = 0.
En déduire l'expression littérale de la distance horizontale parcourue par G correspondant à la longueur d'un pas.
0= -½gL x2 /( v cos a )2 + tan a x.
0= -½gL x /( v2 cos a ) + sin a ; x = 2v2 sin a cos a /gL.
Faire le calcul. Le résultat est-il compatible avec le graphique ? gL= 1,62 m s-2.
x = 2*2,02 sin 60 cos 60 /1,62 = 2,14 ~2,1 m.
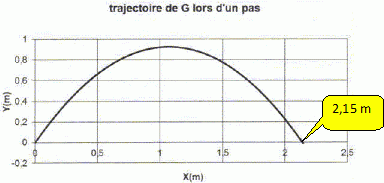
Le résultat du graphe est compatible avec celui du calcul.
|
|