Peut-on
produire un son très aigu à la
limite du
supportable avec une simple tige en
aluminium ? Grâce à la physique des ondes sonores, c'est
parfaitement
possible. Cette expérience étonne un grand nombre de personnes, les
physiciens
eux-mêmes !
Dans une tige métallique, on
peut avoir plusieurs mouvements de vibration qui engendrent un son.
- L’onde est transversale :
la tige oscille autour de son axe. Déformer une tige selon ce mouvement
demande
peu de force. La vibration est de faible énergie d’où un son de basse
fréquence
(note grave).
C’est le même phénomène qui
se produit quand un marteau frappe une plaque de xylophone.
- L’onde est
longitudinale :
la tige se contracte et se dilate le long de son axe. Il faut plus
d'énergie
pour imposer ce mouvement à la tige. La vibration demande plus
d'énergie, d’où
un son de fréquence élevée (note aigüe). C’est le phénomène qui se
produit
quand un archet glisse sur la corde d’un violon.

[..]
On peut ainsi à l’aide de plusieurs
tiges, fabriquer un instrument de musique à condition de respecter les
contraintes imposées par la gamme
tempérée de Bach.
Une gamme musicale est déterminée par
les écarts de fréquence entre les notes qui composent la gamme. Il
existe un
grand nombre de gammes selon leur origine culturelle.
La gamme utilisée dans la musique
occidentale est basée sur « la gamme au tempérament
égal » ou encore
« gamme tempérée » de Jean-Sébastien Bach.
D’après
le
site : www.scienceamusante.net
Dans
cet exercice, l’onde est longitudinale et se propage à la vitesse v
dans la tige.
La section des tiges est un paramètre constant dans tout l’exercice.
|
La
tige est le siège d’ondes stationnaires. Elle se
comporte comme une colonne d’air de longueur L ouverte aux deux
extrémités.
Elle oscille à la fréquence f0
dans son mode fondamental. Son état vibratoire peut alors être
représenté de la
manière suivante :
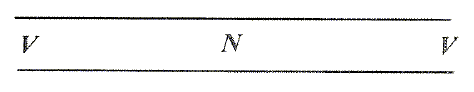
|
Une
tige qui siffle :
La tige est le siège d’ondes
stationnaires.
L’onde est longitudinale. Donner une
définition
de ce type d’onde.
Une onde
est longitudinale lorsque le déplacement des points du milieu de
propagation s'effectue dans la même direction que celle de la
propagation.
Qu’appelle-t-on
onde
stationnaire ?
Lorsqu'une onde
rencontre un obstacle rigide, elle produit une onde réfléchie : 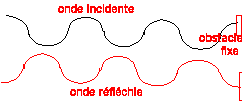
La superposition d'une onde progressive
sinusoïdale de fréquence f et de l'onde réfléchie sur un obstacle fixe
produit une onde stationnaire : une vibration sans propagation, de
fréquence f.
Quelle
relation existe-t-il entre le mode
fondamental et les autres harmoniques ?
Les fréquences des harmoniques sont des multiples de la fréquence du
mode fondamental.
Définir
ce qu’on appelle nœud de vibration.
Un noeud est un point immobile : il ne vibre pas.
On
note l la
longueur d’onde du son de fréquence f. Exprimer l
en fonction de la longueur L
de la tige.
Les ondes stationnaires
s'établissent si la longueur L de la tige est un multiple de la
demi-longueur d'onde l.
2L = nl.
À l’aide d’un microphone, on visualise sur l’écran d’un oscilloscope une
tension électrique, image du mouvement vibratoire de la tige.
Qu’appelle-t-on hauteur d’un
son ?
La hauteur d'un son est
caractérisée par la fréquence du
fondamental.
La tige est en aluminium.
La fréquence du mode
fondamental est égale à 2093 Hz.
Parmi les spectres en fréquence proposés en figure 1 et figure 2 ci-dessous, lequel correspond au son émis, sachant qu’il
s’agit d’un son pur ?
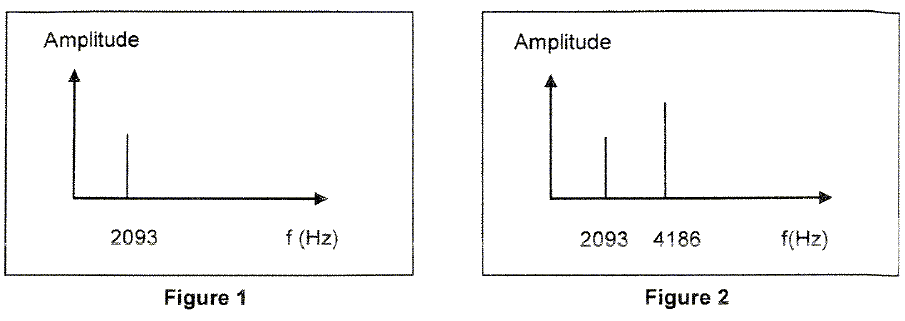
Un son pur ne possède pas d'harmoniques ; le spectre ne possède qu'un seul pic, celui du mode fondamental : donc figure 1.
La
vitesse de propagation v du son à
l’intérieur d’un matériau dépend de certains paramètres, notamment de la masse
volumique de ce matériau.
Répondre par « vrai » ou
« faux » aux affirmations ci-dessous, en justifiant son choix.
Affirmation
1 : Les tiges de même matériau et de longueurs différentes donnent
des notes différentes : la note est plus grave quand la tige est plus
longue. Vrai.
L =½n l = ½n v /f0 ; f0 =n v / (2L) avec v une constante ( même matériau constituant les tiges )
A la tige la plus longue, correspond la fréquence du mode fondamental la plus petite, donc au son le plus grave.
Affirmation
2 : La tige en aluminium donne une note plus aiguë que la tige en
laiton de même longueur. Vrai.
Les
longueurs des tiges sont identiques ; le matériau est différent : à la
plus grande vitesse, correspond la plus grande fréquence du mode
fondamental, donc au son le plus aigu.
On donne les
valeurs de la vitesse du son dans l’aluminium et le laiton.
| Matériau | v (m/s) |
| aluminium | voisine de 4190 |
| laiton ( 70 % Cu ; 30 % Zn ) | voisine de 3470 |
Des tiges musicales.
Dans la gamme de Bach, il y a 12 notes
séparées chacune d’un intervalle appelé « demi-ton ».
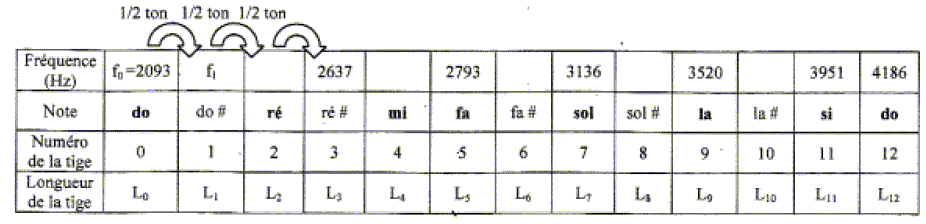
La fréquence f0 est la
fréquence de la note « do » donnée par la tige n°0 de longueur L0.
La fréquence f12 est la
fréquence de la même note à l’octave supérieure. Cette note sera donnée par la
tige n°12 de longueur L12.
Par
définition de l’octave, f12 = 2.f0
Par
conséquent, si k est le rapport de fréquences de deux notes consécutives, k est
égal à 21/12.
k est appelé intervalle ou degré ou
demi-ton. Il est indépendant du couple de notes qui se suivent, d’où le nom de
« gamme tempérée » ou « tempérament égal » pour cette gamme
(tempérament = accord).
|
|
Rappeler la relation qui existe entre la longueur L d’une tige, la vitesse v
de propagation de l’onde dans la tige et la fréquence f du son émis.
L =½n l = ½n v /f ; f = n v / (2L).
La tige numéro 0 a pour longueur L0
= 1,00 m.
Elle
vibre dans son mode fondamental à la fréquence f0 = 2093 Hz.
Par
définition de la gamme tempérée de Bach, la fréquence f1 de la tige n°1 de longueur L1 est donnée par la relation f1 = 2 1/12 f0. Montrer que la longueur L1 s’ écrit : L1 = L0 /
2 1/12.
f1 = 2 1/12 f0 =2 1/12 n v / (2L0).
Or f1 =n v / (2L1), d'où : 2 1/12 n v / (2L0) = n v / (2L1)
2 1/12 / L0 = 1 / L1 ; L1 =L0 / 2 1/12. Ces relations s’écrivent pour la tige n : fn = 2n/12 f0 et Ln
= L0 / 2 n/12.
En s’aidant du tableau ci-dessous, quelle serait la fréquence de la tige la
plus courte ? Retrouve-t-on la valeur donnée pour la définition de l’octave,
donnée page précédente ?

La tige la plus courte correspond à la plus grande valeur de 2 n/12, c'est à dire à n =12.
L12 = L0 / 2 = 0,50 m.
fn = 2n/12 f0 ; f12 = 2f0=4186 Hz.
Cela correspond bien à la définition de l'octave.
|