Emetteur
radiophonique
Étude
du signal à transmettre
Au cours d'un
vide grenier, un
élève achète un diapason dont il veut vérifier la fréquence car il veut
l'utiliser pour accorder son instrument de musique. Pour cela, il
frappe la
fourche du diapason qu'il a placé devant un microphone relié à un
système
d'acquisition par ordinateur. Il visualise
alors, à l’aide d'un
logiciel adapté, le signal musical correspondant au son du diapason.
Mesurer
la
période T sur la figure et calculer la
fréquence f du signal musical.
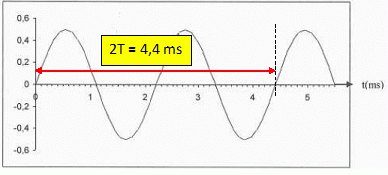
T = 2,2 10-3 s ; f = 1/T =1 / 2,2 10-3 =4,5 102 Hz.
Le diapason était accordé
car la note émise est un La3 (note de référence pour les
musiciens). Ce
signal musical est-il un son complexe ou un son pur ? Justifier.
Le signal est sinusoïdal : il s'agit d'un son pur.
|
Étude du
signal émis
L'élève décide de
transmettre ce signal musical de fréquence f = 440 Hz
et réalise une modulation d'amplitude à l'aide d'un multiplieur. il
visualise
le bon fonctionnement du matériel à l'aide d'un logiciel d'acquisition
et
obtient l'oscillogramme ci-dessous sur lequel il identifie :
- um
(le signal à transmettre) d'amplitude 0,5 V
- us (le signal de
l'onde porteuse modulée en amplitude)
- l'enveloppe
de us
|
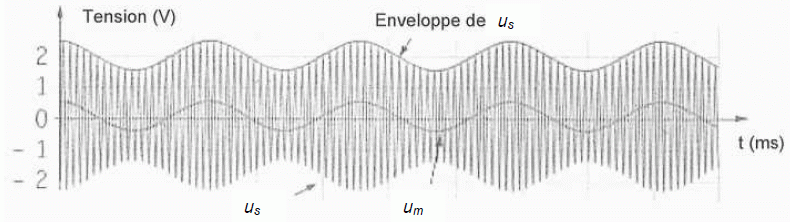
À
partir de l'oscillogramme,
expliquer pourquoi la modulation est satisfaisante.
Le signal modulant à transmettre a la même allure que l'enveloppe : la
modulation d'amplitude est satisfaisante.
Pour
réaliser la modulation, l'élève a ajouté une tension continue E = 2 V au signal à transmettre um.
En
déduire la valeur du
taux modulation m du multiplieur
défini comme le quotient de l'amplitude de um
par la tension continue E.
Amplitude su signal um : 0,5 V.
Taux de modulation m = 0,5 / 2 = 0,25.
Le taux de modulation étant inférieur à 1, la modulation d'amplitude
est correcte.
Quelle
allure aurait eu la modulation si l'élève avait ajouté une tension
continue E inférieure à 0,5 V
? (On pourra faire
un dessin).
Le taux de modulation serait supérieur à 1 : on aurait une
surmodulation.
Le signal modulant à transmettre n'aurait pas la même allure que
l'enveloppe.
Étude
du spectre du signal émis
On réalise le
spectre de us. On obtient la figure
ci-dessous.
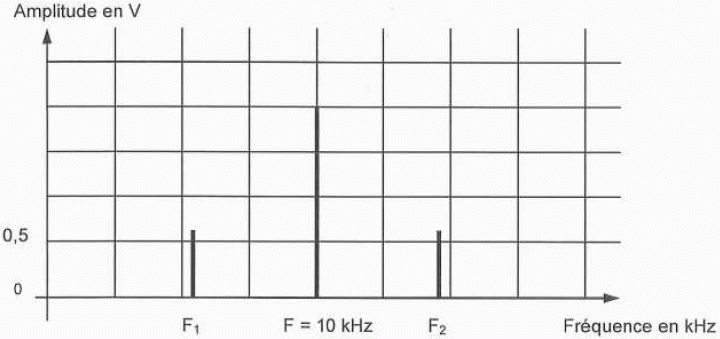
Exprimer
les fréquences F1, F2 indiquées sur la
figure en fonction des
fréquences F de la porteuse et f du signal à transmettre.
F1 = F-f et F2 = F+f.
La
largeur de la bande passante D f
nécessaire pour transmettre la note émise par le diapason est définie
comme la
différence entre F2 et F1. Calculer sa valeur.
Df = F2 -F1
=F+f -F+f = 2 f = 2*440 = 880 Hz.
Récepteur
radiophonique
Au
cours de ce même vide grenier, l'élève a déniché un poste de radio
ancien
permettant l'écoute des stations émettant en modulation d'amplitude
comme France
Inter pour un réglage sur 164 kHz.
En
démontant le poste pour le nettoyer, il a identifié les étages suivants
:
-
Capteur ; -
Amplificateur ; -
Démodulateur ; -
Haut-parleur.
Le
capteur d'ondes électromagnétiques
Ce
capteur est équivalent à une bobine d'inductance L
associée en dérivation avec un condensateur de capacité variable C.
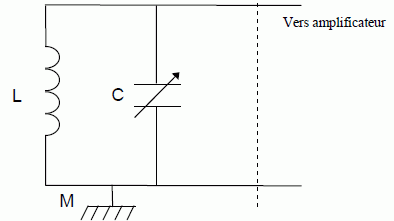
Pour
une valeur donnée de C, ce circuit
permet une bonne écoute de France Inter. Quelle est alors la
valeur de la
fréquence propre f0 du
circuit (L,C) ?
Le capteur a la
même fréquence que la porteuse : f0 = 164 kHz.
L'expression
de la fréquence propre f0 d'un tel capteur est f0 = 1/ (2p(LC)½).
Calculer
la valeur de la capacité C du condensateur permettant
de capter
France Inter si L = 2,0 mH.
C = 1 / (4p2f02L)
= 1 / (4*3,142 *(1,64 105)2 *0,002) = 4,7 10-10 F.
Lors
du nettoyage du poste, l'élève s'aperçoit que le condensateur de
capacité variable C
est lié mécaniquement au bouton de sélection des stations de radio, justifier
cette connexion.
En tournant le bouton, on modifie la valeur de la capacité du
condensateur. En conséquence la fréquence f0 va changer
: cela permet de sélectionner une porteuse, donc une station
radio.
|
|
Le démodulateur
est constitué
d'une diode, d'un conducteur ohmique de résistance R '
et d'un condensateur de capacité C '.
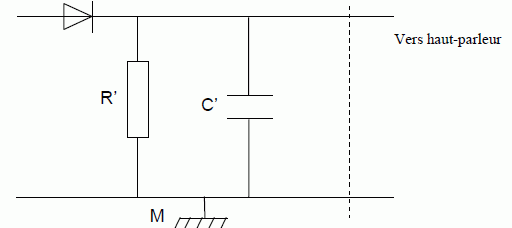
Le
dipôle (R ', C ') est un détecteur d'enveloppe. Montrer
que le produit R '.C ' est homogène à un
temps.
[R']
: tension / intensité soit V A-1. [C']= q/u = charge /
tension soit intensité* temps / tension ou A s V-1.
[R'C' ]= V A-1
A s V-1 soit s.
Pour
avoir une bonne détection, il faut que la constante de temps t
= R'.C' satisfasse la double
inégalité suivante :
Tp << t
< Tm avec :
- Tp
la période de la porteuse.
-
Tm
la période du signal sonore.
Le
conducteur ohmique a une résistance R'
de 15 kW, les ondes sonores ont une fréquence moyenne f
= 1,0 kHz.
Déterminer la
valeur de la capacité C' permettant
de respecter au mieux la condition
indiquée parmi le choix suivant : 50 pF, 50 nF et 50 µF. Ce choix sera justifié par un calcul.
Tm = 1 / f = 1,0 10-3 s.
t < Tm
soit R'C' < 1,0 10-3
; C' < 1,0 10-3
/ 15 103 ; C' >> 6,7 10-8 F
C' < 67 nF.
TP = 1 / 164000 =6,1 10-6
s.
t >> TP soit R'C'
>> 6,1 10-6 ; C' >> 6,1 10-6 / 15 103 ;
C' >> 4,1 10-10 F
C' >> 410 pF.
Seule la valeur C' = 50 nF convient.
|




