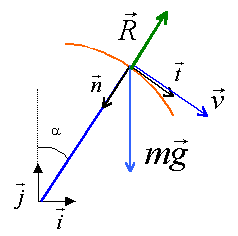QCM : oscillateurs, bille sur une sphère, impulsion, concours kiné. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

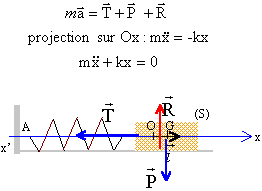
Un athlète a parcouru un 100 m en 10,5s. On modèlise sa course en considérant 2 phases : il accélère uniformément pendant les 15 premièrs mètres de course, qu'il parcourt ensuite à vitesse constante de 11 m/s jusqu'à l'arrivée. - Quelle est la valeur de l'accélération moyenne (m/s²) pendant la phase de démarrage ? 0,95 ; 0,12 ; 9,5 ; 5 ; 6,7 ; 4,0. a = v2/(2x0) =112 / (2*15) = 4,0 m s-2. Un oscillateur mécanique : Il est constitué d'un ressort horizontal de raideur k  ; l'une des extrémité est fixe ; à l'autre extrémité on fixe un solide de masse m. Les frottements sont négligés ; on écarte le solide de sa position d'équilibre et on le lâche sans vitesse initiale. Quelles grandeurs dépendent de la masse ? - l'amplitude du mouvement faux ; - l'énergie cinétique maximale faux ; La conservation de l'énergie mécanique donne : Ec max = ½k A2 avec A, l'amplitude. - la période des oscillations vrai ; T = 2p ( m/k)½ ; - la vitesse maximale vrai ; La conservation de l'énergie mécanique donne : Ec max =½mv2max = ½k A2 ; v2max =k A2 / m ; - l'énergie mécanique  faux ; ;  Conservation de l'énergie mécanique : Em = Ec + Ep = ½mv2+½k x2 =½k A2. Un oscillateur mécanique : Il est constitué d'un ressort horizontal de raideur k = 20 N m-1 ; l'une des extrémité est fixe ; à l'autre extrémité on fixe un solide de masse m = 0,2 kg. Les frottements sont négligés ; on écarte le solide de sa position d'équilibre x0 = 4 cm et on le lâche avec  une vitesse initiale v0=3 m/s, dirigée vers la position d'équilibre. Quelle est l'équation du mouvement dans le système SI ? pulsation w = (k / m)½ = (20 / 0,2)½ =10 rad/s. Conservation de l'énergie mécanique : ½kx02 + ½mv02 = ½kA2 avec A, l'amplitude. A2=x02 +m / k v02 =0,042 +0,2/20 *32 =9,16 10-2 ; A =3,0265 10-1 m ~0,30 m. Phase  à l'origine : x = A cos (wt + f) x(0) = 0,04 = 3,0265 10-1cos f ; cos f = 0,1321 ; f =+1,438 rad ou -1,438 rad. vitesse  : x' = -Aw sin (wt + f) ; vitesse initiale : -Aw sin ( f) = -3 ; la vitesse initiale est dirigée en sens contraire de l'axe Ox sin ( f) =3 / (0,30265*10) =0,991 ; f =+1,438 rad. x(t) =0,30 cos (10t + 1,44) Or cos ß = sin (½p-ß) ; cos (10t + 1,44) = sin (1,57 -10t-1,44) = sin (-10t +0,13) = -sin(10t-0,13) x(t) =0,30 cos (10t + 1,44) = -0,30 sin(10t-0,13).   Oscillateurs :   m = 100 g ; les ressorts sont identiques de raideur k = 30 N / m, de longueur à vide l0 = 20 cm. 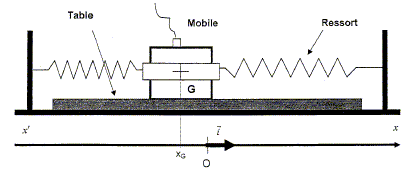Quelle est la pulsation w (rad/s) du système {masse ressorts}? (0 ; 1,54 ; 0,77 ; 17,32 ; 24,5 ). Les deux ressorts sont équivalents  à un ressort unique de raideur 2k. w =(2k/m)½ = (60 / 0,1)½ =(300)½ =10 x 6½ =24,5 rad/s. 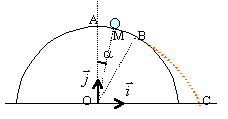Bille sur une sphère. La bille de masse m est initialement au repos en A.Elle glisse sans frottement le long de la sphère de rayon OA = 50 cm. Calculer l'angle a pour lequel la bille quitte la sphère. ( 22° ; 27° ; 48° ; 37°; 90° ) ; expression de la vitesse en M : origine des altitudes, le point O. Ecrire la conservation de l'énergie mécanique : mg OA = mgOAcos a + 0,5 m vM² vM²= 2gOA(1-cos a ) expression de l'action du support en M : th du centre d'inertie projeté sur le vecteur n de la base de Frenet. -R + mgcos a = m v²M / OA remplacer vM²par 2gOA(1-cos a ) R= mg(3cos a -2) en B plus de contact avec le support donc R=0 3cos a = 2 --> a0 = 48,18 ° ~48°. Un footballeur tire un penalty. La masse du ballon est m= 0,453kg. La force d'impact supposée constante est de 250 N et sa durée est Dt= 20 ms. Quelle est la vitesse (m/s) du ballon juste après son départ ? ( 0,8 ; 2,4 ; 6,7 ; 11 ; 15,3 ) variation de quantité de mouvement consécutive à l'action d'une force :  Impulsion  I = F Dt = 250 * 0,020 = 5  N s Quantité de mouvement initiale p =mv = 0 ( vitesse nulle) quantié de mouvement finale : p = mv variation de la quantité de mouvement : mv-0 = mv théorème du centre d'inertie ou généralisation de la seconde loi de Newton pour un système quelconque  : I = mv dans ce cas : v = I/m = 5 / 0,453 =11 m/s.

retour -menu