Le refroidissement en thermodynamique : concours Mines  2010 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Au travers de trois sous-parties indépendantes, on s’intéresse à divers procédés de refroidissement. On rappelle, pour un gaz diatomique, les expressions des capacités thermiques molaires respectivement à volume et pression constante : CVm =2,5 R et Cpm =3,5 R avec R = 8,3 J.mol–1.K–1 : constante du gaz parfait. Détente d’un gaz dans l’atmosphère. Une mole de dioxygène, considéré comme un gaz parfait diatomique, se trouve à la pression P = 2,0 bar et à la température T = 280 K. On lui fait subir une brusque détente dans l’atmosphère de pression supposée constante P0 = 1,0 bar. Par quel(s) qualificatif(s), parmi les suivants, peut-on qualifier la transformation que subit la mole de dioxygène ? On justifiera sa réponse. - réversible ; (Faux) : la réversibilité implique une succession d'états d'équilibre et non pas une détente brutale. - irréversible ; (Vrai) : la détente est brutale. - isotherme ; ( faux) le texte ne précise pas que la température est constante. - adiabatique ; ( vrai) la détente est rapide, les échanges de chaleur entre le gaz et le milieu extérieur n'ont pas le temps de s'établir. - isobare ; ( faux) la pression change. - isochore ; ( Faux) lors de la détente le volume augmente. Par application du premier principe de la thermodynamique, déterminer la valeur de la température T’ atteinte par le gaz à la fin de la détente. On remarquera que P = 2 P0. Travail élémentaire reçu par le gaz lors d'une transformation élémentaire quelconque : dW= -p0dV d'où W= -p0 (V'-V0). Equation des gaz parfaits : au départ 2P0 V = n RT (1). à la fin : P0V' = nRT' (2) avec  V' volume final et T' température finale. (2) divisé par (1) donne V'= 2V T' / T. repport dans l'expression du travail : W= -p0V(2T ' /T-1). Exprimer de 2 manières différentes l'énergie interne : DU = W+Q avec Q=0,  système adiabatique irréversible. DU = -p0V(2T '/T-1) (3) DU = nCvm(T '-T) avec n = 2p0V /(RT ) et Cvm =2,5R DU = 2p0V 2,5 R / (RT)  (T '-T) = 5p0V  (T '/T-1) (4) écrire (3) = (4) d'où : -p0V(2T '/T-1) =5p0V  (T '/T-1) -2T '/T+1= 5T '/T-5 ; T' = 6/7 T = 6*280 / 7 = 240 K. La température finale du gaz diminue. Exprimer la variation d’entropie du gaz lors de cette transformation. dU=TdS-pdV = nCvmdT dS= nCvm /T dT+p/T dV = nCvm /T dT+nR/V dV ; pour la transformation globale : D S = nCvm ln(T '/T)+nR ln( V'/V) n= 2p0V /(RT ) ; V '/V= 2 T ' / T= 12 / 7 ; Cvm = 2,5 R. D S = 2p0V /T [ 2,5  ln (6 / 7) + ln (12 / 7)]   Climatisation d’un local. Un cycle de Brayton inversé réalise un effet frigorifique. Lors de ce cycle, un gaz est comprimé, refroidi puis détendu. La température de fin de détente étant basse, ce gaz peut être utilisé pour refroidir une enceinte, soit par contact direct (notamment s’il s’agit d’air), soit par l’intermédiaire d’un échangeur. Ce type de dispositif a été jusqu’à récemment très utilisé dans les avions pour assurer la climatisation des cabines en vol. Il est également utilisé pour climatiser les très grosses installations qui nécessitent de grandes quantités de fluide caloporteur. Un cycle de Brayton inversé est formé de deux adiabatiques et de deux isobares. Il est supposé réversible et décrit par de l’air (assimilé à un gaz parfait diatomique). Dans cet exercice on considérera une mole d’air parcourant le cycle. On appelle γ le rapport des capacités thermiques à pression et volume constants. • 1 --> 2 : compression adiabatique réversible faisant passer le gaz de la pression P1 à la pression P2 ; • 2 --> 3 : compression isobare ; • 3 --> 4 : détente adiabatique réversible redonnant la pression P1 au gaz ; • 4 --> 1 : retour isobare au point 1. Tracer dans un diagramme de Clapeyron (ou diagramme P,V) le cycle de Brayton inversé. Justifier le fait qu’il soit adapté pour décrire un climatiseur. 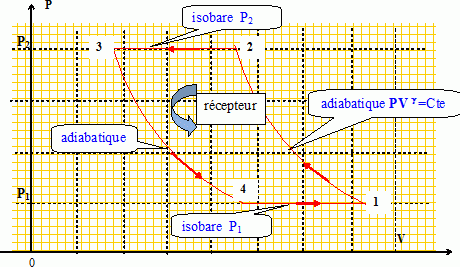 Justifier sans calcul lourd le fait que la transformation 2 --> 3 s’accompagne d’un refroidissement. Equation des gaz parfaits écrite pour l'état 2 et l'état 3 : P2V2 = nRT2 d'où T2 = P2V2 /( nR ). P2V3 = nRT3 d'où T3 = P2V3 /( nR ). Lors de la compression isobare 2-->3, le volume diminue V3 < V2 ; par suite T3 est inférieure à T2. Pour les quatre transformations du gaz envisagées, exprimer le transfert thermique associé en fonction de R (constante du gaz parfait) et des températures Ti (i = 1,2 ,3 ou 4) nécessaires. Pour les adiabatiques 1--> 2 et 3 -->  4, le transfert thermique est nul. Q23 =Cpm( T3-T2) = 3,5 R ( T3-T2) et Q41 =Cpm( T1-T4) = 3,5 ( T1-T4). Soit η l’efficacité du climatiseur. Définir η puis l’exprimer en fonction des transferts thermiques des différentes transformations du cycle. L 'efficacité est l'énergie qu'il faut retirer de la source chaude Q41( local à climatiser ) divisée par le travail investi ( lors de la compression du fluide ). W + Q23 +Q41 =DUcycle = 0 d'où : W = -(Q23 +Q41) h = |Q41  / (- Q23 -Q41)|  On pose a = P2 / P1, appelé rapport de compression du cycle. Exprimer de nouveau η uniquement en fonction de a et de γ. h =|( T1-T4)  / (-T3+T2 -T1+T4)|  = | 1 / ((T2 -T3  / ( T1-T4)-1) | adiabatique réversible 1 --> 2 : T1 P1(1-g)/g = T2 P2(1-g)/g  ; adiabatique réversible  3 --> 4 : T3 P3(1-g)/g = T4 P4(1-g)/g  ; Or P2 = P3 et P4 = P1 : T3 P2(1-g)/g = T4 P1(1-g)/g  ; T1 = T2 a(1-g)/g  ; T4 = T3 a(1-g)/g  ; T1-T4 =  (T2 -T3 )a(1-g)/g  ; η = 1 / (1-a) (1-g) / g. Utilisation des transitions de phase de l’eau. On met de l’eau chauffée à la température T1 = 300 K dans une bouteille de volume V0, en ne remplissant la bouteille qu’au quart de sa capacité. La bouteille est ensuite fermée. On suppose que l’air enfermé avec l’eau dans la bouteille est parfaitement sec à l’instant initial et qu’il n’y aura pas de transfert thermique avec l’extérieur. On donne : Psat= 70,0.102 Pa, la pression de vapeur saturante de l’eau, supposée constante dans l’intervalle de température étudié ; LV = 3,00.106 J.kg–1 la chaleur massique de vaporisation de l’eau ; ceau= 4,20.103 J.K–1.kg–1 la chaleur massique de l’eau liquide ; Meau = 18 g.mol–1 la masse molaire de l’eau ; ρ = 1000 kg.m–3 la masse volumique de l’eau liquide. Qualitativement, que va-t-il se passer dans la bouteille ? Que peut-on prévoir quant à la température finale du système ? La température du liquide s'élève ; de la vapeur d'eau apparaît au dessus du liquide. Quand la pression  partielle de la vapeur d'eau sera égale à la pression de vapeur saturante de l'eau, la vapeur et le liquide seront en équilibre. L'évaporasation de l'eau nécessite un apport d'énergie : c'est le liquide qui fournit cette énergie ; le liquide se refroidit. Au vu de la valeur numérique de T1, que pouvez-vous dire de la quantité de matière de l’eau liquide qui va s’évaporer ? Que peut-on en déduire sur le volume de ce liquide restant à l’équilibre ? A 300 K , très peu de liquide s'évapore ; le volume du liquide peut être considéré comme constant. On considèrera dans ce problème comme négligeables les chaleurs massiques de l’eau vapeur et de l’air vis-à-vis de celle de l’eau liquide. On admettra aussi que la transformation a lieu approximativement à P et V constants. On appelle Teq la température à l’équilibre Exprimer en fonction de V0, R, Teq, Psat et Meau la masse d’eau qui a été vaporisée me v, à l’équilibre. On suppose que la vapeur d'eau  ( pression Psat , volume 0,75 V0, température Téq )se comporte comme un gaz parfait : Psat 0,75 V0 = n RTéq avec n = me v / Meau. Psat 0,75 V0 = me v / Meau RTéq ; me v  = 0,75PsatV0 Meau / (RTéq ).   À l’aide d’un bilan énergétique et en négligeant tout transfert thermique avec l’extérieur, en déduire une expression de la variation de température DT = Téq-T1. L’évaluer numériquement en supposant que DT = Téq-T1 << Téq. Masse de liquide m L = reauV0/4 ; énergie cédée par l'eau : m L ceau DT ; énergie gagnée par la vapeur d'eau : me v Lvap ; Système supposé adiabatique : m L ceau DT +me v Lvap  = 0  ; DT  = - me v Lvap  / m L ceau = - 4 me v Lvap  / (reauV0 ceau ) Puis remplacer me v par 0,75PsatV0 Meau / (RTéq ) : DT  = - 3 Psat Meau Lvap  / (reau ceau RTéq ) =-3*7000 *0,018 * 3,00.106 / ( 1000 *4200*8,3*300) = -18*3 103 /(2*8,3*3 104) = -1,8 / 16,6 ~ -0,11 K. Dans un laboratoire, pour obtenir un effet de refroidissement accru, on place dans un récipient aux parois athermanes (interdisant les transferts thermiques) une masse m0 d’eau liquide, à la température T0. La vapeur formée est éliminée par une pompe qui l’aspire lentement. Expliquer qualitativement ce qui va se passer. La vapeur d'eau étant lentement retirée du récipient, la pression de la vapeur ne peut pas atteindre Psat : - toute l'eau va donc s'évaporer, ou bien on va atteindre le point triple. On cherche à évaluer les variations de masse de l’eau liquide. L’évaporation d’une masse dm d’eau provoque une variation de température dT à l’intérieur du récipient.  Écrire l’équation différentielle liant m(T), dm et dT. énergie cédée par l'eau : (m0-dm) ceau dT ; énergie gagnée par la vapeur d'eau : dm Lvap ; Système athermane : (m0-dm) ceau dT +dm Lvap  = 0. ou m ceau dT +dm Lvap  = 0 avec m = m0-dm.  Pour le domaine de température considérée, LV est une fonction affine de la température : LV=a - bT, avec a et b des coefficients positifs. En déduire l’expression de la masse d’eau m(T) présente à la température T. dm / m = -ceau / Lvap dT d (ln m) = -ceau dT / (a-bT) = ceau / b d (ln (a-bT)) ln m = ceau / b ln (a-bT) + cste. ln m0 = ceau / b ln( a-bT0) + cste ; ln (m / m0) = ceau / b ln ((a-bT) / (a-bT0)) m = m0 ((a-bT) / (a-bT0))ceau / b. .

menu