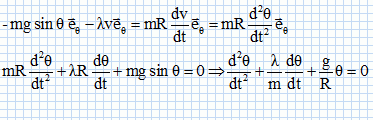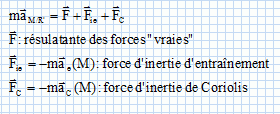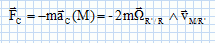|
Mouvement
d'un point matériel sur un rail circulaire : concours Mines 2010 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|||||||
| .
. |
|||||||
|
|||||||
|
Un petit objet assimilé à un point matériel M, de masse m, peut glisser sans frottement le long d’un rail ayant la forme d’un demi-cercle de centre O et de rayon R, placé dans un plan vertical. Le rail est d’abord supposé fixe par rapport au référentiel terrestre ℜ galiléen. On repère la position du point M à l’instant t par l’angle θ. À l’instant t = 0, l’objet est lancé du point M0 avec une vitesse v0. Dans tout le problème, on utilisera une base de projection polaire (er ; eq). On prendra pour valeur de l’accélération de la pesanteur g = 10 m.s-2. Faire l'inventaire des forces appliquées à M et le représenter ; préciser les composantes de ces forces dans la base polaire. Le mobile est soumis à son poids et à l'action du support. 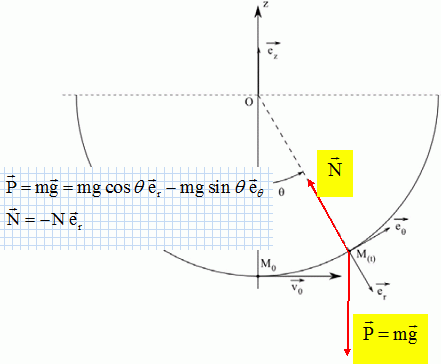 En déduire l'équation différenteile à laquelle satisfait la fonction q(t). 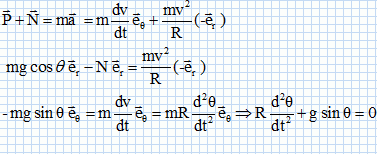 On suppose que la norme v0 du vecteur vitesse initial est suffisamment faible pour que la condition |q(t)|<<1 rad soit satisfaite à chaque instant. Déterminer complètement l'expression de q(t) en fonction de v0, R g et t. sin q ~q exprimé en radian. R d2q/dt2 + gq = 0. Solution générale : q = A sin((g/R)½ t + j), A et j étant des constantes. q(0) = 0 = A sin j ; A n'étant pas nul, alors j = 0. vitesse : v = Rdq/dt = (gR)½A cos((g/R)½ t) ; vitesse initiale : v0 = (gR)½A ; A = v0(Rg)-½. q = v0(Rg)-½ sin((g/R)½ t ).
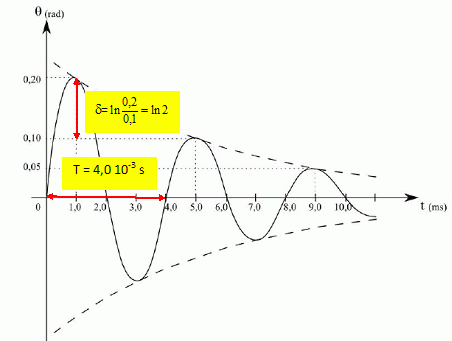
Les grandeurs m, g et R étant fixées, donner la condition portant sur λ pour que le mouvement soit pseudo-périodique. Equation caractéristique associée à l'équation différentielle : r2 +l/m r +g/R =0. (1) Le discriminant D doit être négatif pour avoir un mouvement pseudo-périodique : D = (l/m)2 -4g/R ; (l/m)2 <4g/R ; l/m < 2(g/R)½ ; l < 2m(g/R)½ ; On suppose cette condition réalisée. Exprimer θ sous la forme q(t) = A exp(-t/t) sin(Wt). On justifiera soigneusement l’établissement de cette relation et on exprimera A,τ et Ω en fonction de v0, m, g, R et λ. On pose w02 = g/R ; D = 4(l / (2m))2 -4w02 ; on pose W2 = [w02 -(l / (2m))2 ] ; par suite D = 4 j2W2 avec j2 = -1. Solution de (1) : r1 = -l / (2m) +jW ; r2 = -l / (2m) -jW ; Les solutions de l'équation différentielle sont donc : q(t) = Aexp(r1t) + B exp(r2t)avec A et B des constantes. q(t) =exp(-l t/ (2m)) [A exp( jW t)+ Bexp( -jW t)]. Cette solution peut s'écrire sous la forme : q(t) = C exp(-l t/ (2m)) sin (Wt+F) avec C et F des constantes déterminées par les conditions initiales. q(0) = C sin (F) = 0 d'où F = 0. La vitesse initiale est égale à v0 = Rq'(0) ; q'(t) = -C l / (2m) exp(-l t/ (2m)) sin (Wt) + C Wexp(-l t/ (2m))cos (Wt) v0 = Rq'(0) = R C W ; C = v0 /(R W). q(t) = v0 /(R W) exp(-l t/ (2m)) sin (Wt) avec t = 2m / l.
|
|||||||
| |
|||||||
|
|
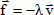 , où λ est une constante positive et v
le vecteur vitesse du point M à l’instant t. L
, où λ est une constante positive et v
le vecteur vitesse du point M à l’instant t. L