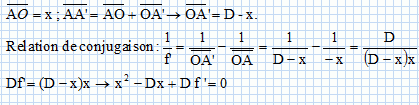Lentille convergente, dispersion, réfraction.

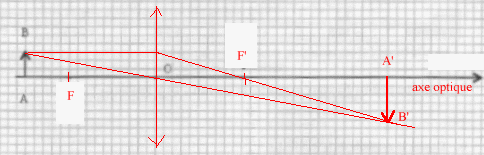
Si on ne peut pas disposer d’un projecteur de diapositives, il est possible de réaliser une projection avec une lentille convergente. On dispose d’une lentille convergente de distance focale 25 cm. On souhaite projeter l’image sur un écran vertical situé à 5,0 m de la lentille. L’axe optique de la lentille est perpendiculaire à l’écran et au plan de la diapositive. La diapositive étant carrée, de 30 mm de côté, quelle est la dimension de l’image visualisée sur l’écran ? ( 27 cm ; 36 cm ; 57 cm ; 78 cm ; 1,1 m ) 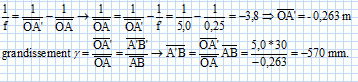Utiliser la formule de conjugaison pour trouver la position de la diapositive AO. La dimension de l'image est donc 57 cm. Une étoile émet une puissance lumineuse de 8.1024 W dans toutes les directions de l’espace. Quelle est la puissance lumineuse reçue par l’objectif d’un télescope de diamètre D = 1 m situé à 5.1013 km du centre de l’étoile en admettant qu'il n'y a aucune atténuation sur le trajet ? 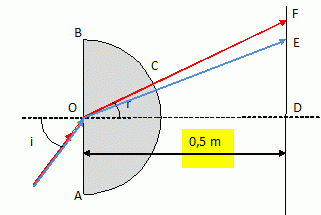( 2.10-10 W ; 5.10-5 W ;  8.10-5 W ; 2.10-4 W ; 0,2 W ) 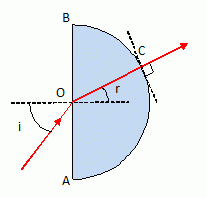Surface S d'une sphère de rayon R = 5 1013 km = 5 1016 m. S = 4 p R2 = 4*3,14 *(5 1016)2 =3,14 1034 m2. Surface, notée s, de l'objectif du téléscope : s = p D2/4 = 3,14 / 4 =0,785 m2. s / S = 0,785 / 3,14 1034 =2,5 10-35. Puissance reçue par l'objectif : 8.1024 *2,5 10-35=2.10-10 W Dispersion. Un faisceau de lumière blanche est envoyé sur un bloc de verre hémi-cylindrique de rayon R =OA=OB=10 cm, sous un angle d'incidence i = 60°. Tracer le chemin suivi par un rayon de lumière jaune de longueur d'onde lJ=1,785 nm ; l'indice du verre pour cette radiation est nJ=1,785. En O, loi de Descartes pour la réfraction : nair sin i = nJ sin r. 1,0 * sin 60 = 1,785 sin r ; sin r = 0,485 ; r = 29°. En C le faisceau est perpendiculaire au dioptre verre-air : il n'est pas dévié. L'indice du verre dépend de la longueur d'onde l : n(l )=a + b / l 2 ; a = 1,740 ; b = 15650 ; l en nm. Calculer les indices du verre pour les radiations limites du spectre visible ( lV =400 nm et lR =780 nm.) nV =1,740 + 15650 / 4002 =1,838. nB =1,740 + 15650 / 7802 =1,766. Le faisceau émergent est observé sur un écran  vertical placé  à D =50 cm  de la face AB. Qu'observe t'on ? ( aspect et  dimension du spectre) En O, loi de Descartes pour la réfraction : nair sin i = nV sin r.  violet : 1,0 * sin 60 = 1,838 sin r ; sin r = 0,471 ; rV = 28,11°.  rouge : 1,0 * sin 60 = 1,766 sin r ; sin r = 0,490 ; rR = 29,36°. DE = OD tan rV =0,5 *tan 28,11 =0,2671 m ; DF = OD tan rR =0,5 *tan 29,36 =0,2813 m ; Largeur de l'arc en ciel observé : 0,2813-0,2671 = 0,0142 m = 1,4 cm.   Web www.chimix.com Distance focale ( méthode de Bessel). L'objet AB et l'écran A'B' sont fixes, distants de D. On note f' la distance focale de la lentille. Recherche des positions de la lentille donnant une image nette. D = D2- 4Df '; si D >0 , il y a deux solutions x1 et x2. Si D >4f : x1 = ½ D+½(D2- 4Df ')½ ; x2 = ½ D-½(D2- 4Df ')½ ; x1 -x2 = (D2- 4Df ')½ ; on note d = x1 -x2 ; d2 = D2- 4Df ' ; f ' = (D2-d2 ) / ( 4 D). ..

retour -menu