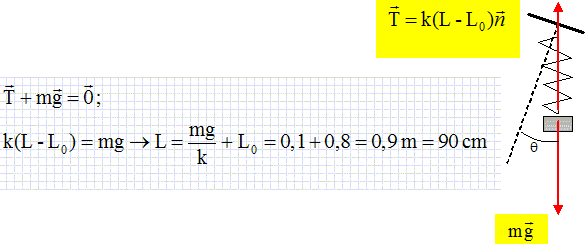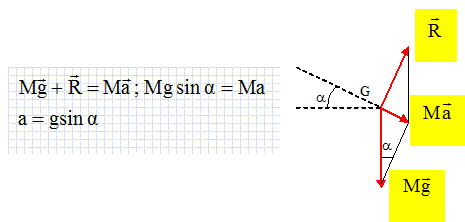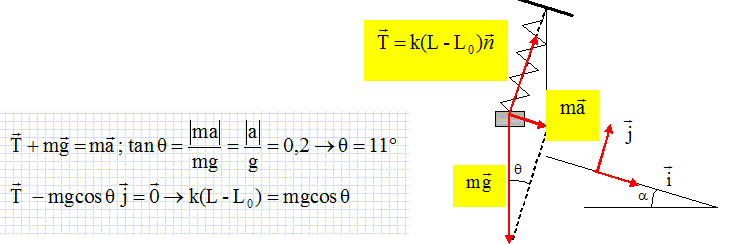Pendules élastiques dans un véhicule : freinage, descente : concours kiné Assas 2010.

. .

. .

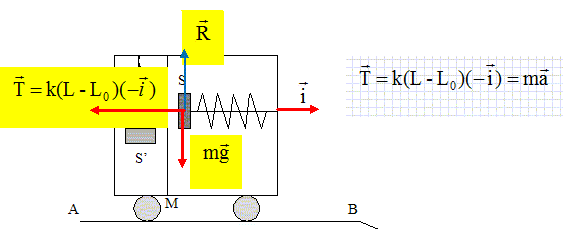
Exercice n°1 Un véhicule à moteur se déplace le lond du chemin rectiligne ABCD. La portion AB est horizontale, la portion BCD est inclinée d'un angle a par rapport  à l'horizontale. On considère deux solides ponctuelsS et S', de même masse m = 100 g. Le solide S est attaché à la paroi intérieur du véhicule par un ressort de raideur k = 10 N/m, de longueur à vide L0 = 80 cm. S peut se déplacer sans frottement le long d'une tige  rigide, fixée au véhicule, parallèle à son vecteur vitesse. L'ensemble constitue un pendule élastique (S). Le solide S' est attaché au plafond du véhicule par un ressort identique au précédent. L'ensemble constitue un pendule élastique (S'). Un fil MN fixé à l'intérieur du véhicule, perpendiculaire au plancher de celui-ci, représente la "verticale" du véhicule. On prendra g = 10 m s-2 et sin a = 0,20. Portion AB du chemin : Le véhicule freine de façon uniforme. Le vecteur accélération de son centre d'inertie a pour norme a = 2,0 m s-2. Représenter les forces appliquées au solide S et calculer la longueur ( en cm) du ressort S. Lors du freinage, la vitesse diminue : l'accélération est négative. k(L-L0)=ma ; L= L0+ ma/k =0,80 -0,1*2/10 =0,78 m = 78 cm.   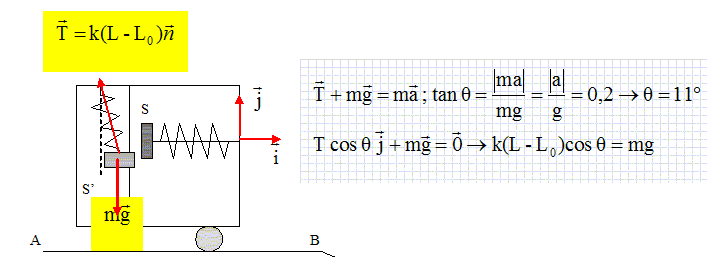Représenter les forces appliquées au solide S' et calculer la longueur ( en cm) du ressort S' et son inclinaison q. L = L0 +mg /(k cos q) = 0,80 +0,1*10 /(10*0,98) =0,90 m = 90 cm.  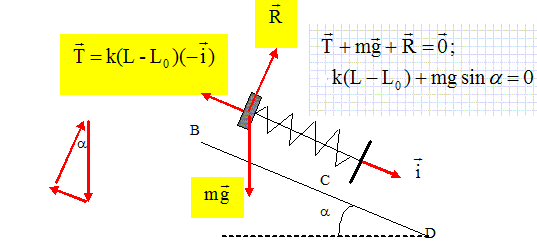Portion BC du chemin :  Le centre d'inertie du véhicule est en mouvement rectiligne uniforme. Calculer la longueur ( en cm) du ressort de (S). D'après le principe d'inertie, la somme vectorielle des forces appliquées au solide S est nulle. Le ressort est comprimé. k(L0-L)=mg sin a ; L = L0 - mg sin a / k = 0,80 - 0,1*10*0,2 / 10 = 78 cm. Représenter les forces appliquées au solide S' et calculer la longueur ( en cm) du ressort S' et son inclinaison q. Le ressort est vertical : q = a =11 °.  Portion CD du chemin : Le moteur du véhicule est arrêté. Le véhicule n'est soumis à aucune force de frottement, mais uniquement  à son poids et aux réactions normales de la chaussée sur les roues. Donner sans démonstration, l'expression de la norme de l'accélération du centre d'inertie du véhicule. Référentiel terrestre supposé galiléen : la vitesse du véhicule augmente lors de la descente ; l'accélérartion est positive : a = g sin a = 10 *0,2 = 2 m s-2. Calculer la longueur ( en cm) du ressort de (S). k(L-L0)=0 ; k n'est pas nul donc L=L0 = 80 cm. Représenter les forces appliquées au solide S' et calculer la longueur ( en cm) du ressort S' et son inclinaison q. Le ressort est dirigé suivant MN : par rapport à MN l'angle est nul. L = L0 +mg cos q/k = 0,80 + 0,1*10*cos11 / 10 =0,80 +0,098 ~ 90 cm.

menu