Raideur d'un ressort, lumière et milieu transparent : concours manipulateur radio Poitiers 2010.

. .

.  .

Exercice 1. On se propose de mesurer la constante de raideur d'un ressort par une méthode dite de la surcharge. On étudie le mouvement d'un solide S de masse M attaché à un ressort de constante de raideur K. Le solide se déplace horizontalement et les frottements sont négligés ; x est l'abscisse de G dans le repère ( O, i ). On écarte horizontalement le solide de sa position d'équilibre d'une distance x0 et à l'instant de date t=0, on l'abandonne sans vitesse initiale. Equation différentielle régissant le mouvement du centre d'inertie G. Faire l'inventaire des forces s'exerçant sur le solide S à l'instant t=0 et les représenter sans souci d'échelle sur un schéma ne comportant que le solide S et les forces qu'il subit. On indiquera bien pour chaque force : son nom, son symbole et ses caractéristiques vectorielles, la norme n'étant exprimée que littéralement. ( on notera g l'accélération de la pesanteur ). 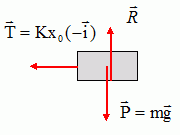P : poids, verticale vers le bas, valeur mg ; R : action du plan, opposée au poids ; T : force de rappel exercée par le ressort, horizontale vers la gauche. Etablir l'équation différentielle du mouvement du centre d'inertie G du solide et montrer qu'elle se met sous la forme x" + k/m x = 0. Ecrire la seconde loi de Nenton : 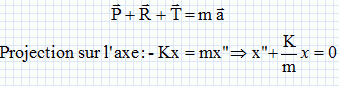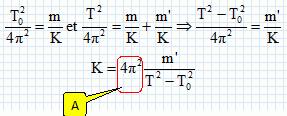On admettra que la solution générale de l'équation différentielle du mouvement du centre d'inertie G du solide, peut s'écrire sous la forme : x(t) = Xmax cos [2p t / T0 +j]. En déduire que l'expression de la période propre T0 en fonction de K et m est : T0 = 2p (m/K)½. Dériver x(t) par rapport au temps : x'(t) = -Xmax 2p  / T0sin [2p t / T0 +j]. Dériver une seconde fois : x"(t) = -Xmax [2p  / T0 ]2 cos [2p t / T0 +j] = -[2p  / T0 ]2 x(t). Repport dans l'équation différentielle : -[2p  / T0 ]2 x(t)+ K/m x(t) = 0 -[2p  / T0 ]2+ K/m = 0 soit : T0 = 2p (m/K)½. On mesure la durée de 15 oscillations, soit Dt = 15,6 s. Calculer T0. Dt / 15 = 15,6 / 15 = 1,04 s.   Le solide S est maintenant surchargé par un autre solide S' de masse m' = 20,0 g, fixé sur S. Ce nouveau système est excité et l'on mesure 15 oscillations en Dt = 16,05 s. Quelle est la nouvelle expression de la période T associée à l'ensemble {S +S'} en fonction de K, m et m' ? Dands l'expression de T0, remplacer m par m+m' : T = 2p ((m+m')/K)½ Calculer T. T = Dt /15 =16,05/15 =1,07 s. A l'aide des questions précédentes, montrer que l'on peut écrire K sous la forme  K = A m' / (T2-T02) avec A une constante à déterminer. Calculer K et m. K = 4*3,142 *0,020 /[1,07-1,04)(1,07+1,04)]=12,5 N m-1. T0 = 2p (m/K)½ ; m = K T02 / (4p2) =12,5 *1,042 / 4*3,142) = 0,34 kg. 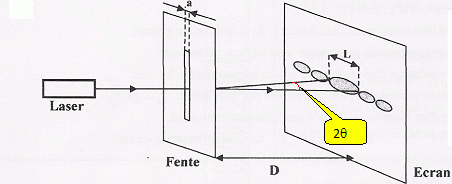Une fente verticale, de largeur a est placée sur le trajet d'un faisceau lumineux produit par un laser. Un écran est placé  à une distance D de la fente. 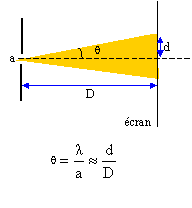Sur l'écran, on observe dans un plan horizontal, une tache lumineuse centrale de largeur L, nettement supérieure à la largeur de la fente ainsi qu'une série de taches lumineuses plus petites de part et d'autre de la tache centrale. q est l'écart angulaire entre le centre de la tache centrale et la première extinction. La distance D étant très supérieire à L, on considère que q est petit et que donc q ~tan q avec q exprimé en radian. Comment s'appelle le phénomène observé ? La diffraction. Quel caractère particulier de la lumière met-il en évidence ? La lumière se comporte comme une onde ( aspect ondulatoire de la lumière ). La lumière émise par le laser est monochromatique. Quelle est la signification de ce terme ? Une lumière monochromatique comporte une seule fréquence, une seule couleur. Première série :  on utilise le même laser et la même distance D entre la fente et l'écran. Expérience 1 :  avec une fente "a1" on mesure la largeur de la fente centrale L1 = 5,0 cm. Expérience 2 :  avec une fente "a2" on mesure la largeur de la fente centrale L2 = 2,0 cm. Laquelle de ces deux expériences est obtenue avec la fente la plus large ? La diffraction est d'autant plus marquée ( L important  que la largeur de la fente est plus petite : L2 < L1, donc "a2" >"a1". Deuxième série :  on utilise le même laser et la fente. Expérience 1 :  la fente est à la distance "D1", on mesure la largeur de la fente centrale L1 = 5,0 cm. Expérience 2 :  la fente est à la distance "D2", on mesure la largeur de la fente centrale L2 = 8,0 cm. Laquelle de ces deux expériences correspond à la plus grande distance entre la fente et l'écran ? tan q ~q = ½L / D avec q constant ( même laser et même largeur de fente). L2 > L1, donc "D2" >"D1". Troisième série :  on utilise la même fente et la même distance entre la fente et l'écran. Expérience 1 : le laser utilisé émet une lumière dont la longueur d'onde dans le vide est l1 = 650 nm, on mesure la largeur de la fente centrale L1 = 3,0 cm. Expérience 2 : le laser utilisé émet une lumière dont la longueur d'onde dans le vide est l2, on mesure la largeur de la fente centrale L2 = 2,2 cm. Calculer l2. l2 = ad/D = aL2 /(2D) ; l1 = aL1 /(2D) ; l2 =l1L2 /L1  = 650*2,2 / 3,0=477 = 4,7 102 nm. On utilise une fente de largeur 1,00 mm placée à 1,60 m de l'écran. Celle-ci est éclairée par un laser dont la lumière &émise a une fréquence de 4,62 1014 Hz. Observe t-on sur l'écran une figure analogue à celles des expériences précédentes ? l =c / f = 3,00 108 / 4,62 1014 =6,49 10-7 nm = 649 nm. largeur de la fente centrale L = 2l D / a =2*6,49 10-7 *1,60 / 1,00 10-3 =2,08 10-3 m = 2,08 mm. La diffraction est très peu marquée, voir inexistante, la fente est trop large. On étudie maintenant la propagation dans différents milieux de la lumière jaune ( de longueur d'onde dans le vide l0 = 590 nm) émise par un laser. La vitesse de propagation de cette onde dans le diamant est v = 1,24 108 m/s. Quelle est  sa fréquence dans le vide ? f = c / l0 = 3,00 108 / (590 10-9) =5,0847 1014 = 5,08 1014 Hz. L'onde émise se propage dans le diamant. Quelle est sa fréquence, sa couleur et sa longueur d'onde ? La fréquence, donc la couleur, sont inchangées. Longueur d'onde l = v / f = 1,24 108 / 5,0847 1014 =2,44 10-7 m = 244 nm. La lumière passe du diamant  à l'eau dont l'indice de réfraction pour la lumière jaune est égal à 1,33. Dans quel milieu ( eau ou diamant ), la lumière se propage t-elle le plus rapidement ? n = c/ v soit v = c / n = 3,00 108 / 1,33 =2,26 108 m/s. La lumière se déplace plus vite dans l'eau que dans le diamant.

menu