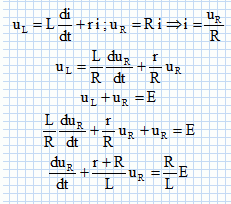Etablissement du courant dans une bobine réelle, concours technicien météo 2009.

. .

.  .

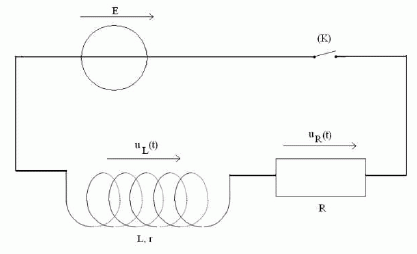(6,5 points) Dans le circuit électrique représenté ci-dessus la bobine est caractérisée par son inductance L et sa résistance r, le générateur délivre une tension constante E, le conducteur ohmique est caractérisé par sa résistance R. A t = 0 s on ferme l’interrupteur (K). On note uR(t) la tension aux bornes du conducteur ohmique, uL(t)la tension aux bornes de la bobine et i(t) le courant circulant dans le circuit. Expliquer pourquoi uR(t) = 0 V lorsque t = 0 s.. uR (t)= R i (t); Avant la fermeture (t=0-) de l'interrupteur, la bobine ne stocke pas d'énergie. Juste après la fermeture de l'interrupteur (t=0+) : la continuité de l'énergie stockée par la bobine conduit à : i(t=0+) =i(t=0-) =0. Par suite : uR (t=0+)= R i (t=0+) = 0.   Ecrire la relation liant uL(t), uR(t) et E. Additivité des tensions : uL(t) + uR(t) =E. Exprimer uL(t) en fonction de i(t), L et r ; puis en fonction de uR(t), R, r et L.  Déduire de ce qui précède l’équation différentielle. Vérifier que uR(t) = ER/(R+r) (1-exp(-t / t)) avec t = L/(R+r) est solution de l'équation différentielle ; vérifier que uR(t=0) = 0. Dériver par rapport au temps : u'R =ER / L exp(-t / t). Repport dans l'équation différentielle : ER / L exp(-t / t)+ER / L (1-exp(-t / t)) = RE/L. ER / L exp(-t / t) -ER / L exp(-t / t) +ER/L = RE / L ; égalité vérifiée quel que soit le temps. uR(0) = ER/(R+r) (1-exp(-0 / t)) = ER/(R+r) (1-1) =0. Nommer et calculer τ ; montrer grâce à une analyse dimensionnelle que τ est homogène à une durée. t est la constante de temps du dipôle (RL). énergie : ½L I2 ; L : énergie divisée par une intensité au carrée énergie libérée par effet Joule : RI2t ; R est une énergie divisée par un temps et une intensité au carré. Par suite [t] = J A-2 J-1 T A2 soit : [t] =T. Calculer uR(t = τ) et uR(t = 5τ). Commenter. uR(t = infini) = ER/(R+r) = uR max. uR(t = τ) = ER/(R+r) (1-exp(-1) =0,63 ER/(R+r) = 0,63uR max. uR(t = τ) est égal  à environ 2/3 de sa valeur maximale. uR(t = 5τ) = ER/(R+r) (1-exp(-5) =0,007 ER/(R+r)= 0,007 uR max. uR(t = 5τ) est pratiquement égale  à sa valeur maximale (  à 1 % près). La durée du régime transitoire est pratiquement terminée ; la bobine stocke le maximum d'énergie.  Calculer l’énergie Wm emmagasinée par la bobine à t = 5τ. Données : E = 10 V, R = 1,5 kW, L = 30 mH et r ~ 0 ? En régime permanent, l'intensité est constante et vaut I : dI/dt = 0 d'où E = rI + RI soit I = E/(R+r) = 10 / 1500 =6,667 10-3 A. Wm = ½LI2 = 0,5 * 0,030 *(6,667 10-3)2 =6,67 10-7 J ~ 6,7 10-7 J. ....

retour -menu