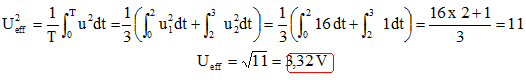Thévenin, valeur moyenne, valeur efficace, concours marine marchande filière professionnelle machine 2004

Aurélie 22/12/09

Thévenin, valeur moyenne, valeur efficace, concours marine marchande filière professionnelle machine 2004.

. .

.
.

Question 3 (5 points)

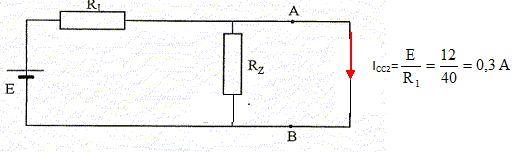
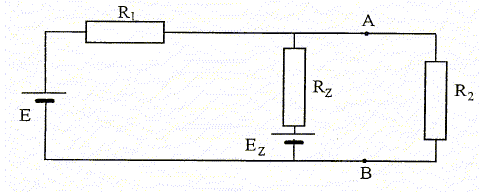On donne : E = 12 V ; Ez = 6 V ; R₁ = 40 Ω ; Rz = 4 Ω.
Déterminer le modèle équivalent de Thévenin du dipôle AB qui alimente la résistance R₂.
On enlève les sources ; R₁ et Rz sont alors en dérivation ; on note R_th la résistance équivalente :
R_th = R₁ Rzc/(R₁+Rz) = 40*4 / 44 = 3,636 ~3,6 W.
On rétablit les sources et on met R₂ en court-circuit. On note I_cc l'intensité traversant le fil AB.
Calcul de I_CC : ( méthode de superposition )
On enlève E ; on note I_CC1 l'intensité du courant traversant le fil AB. ( R₁ est court-circuitée )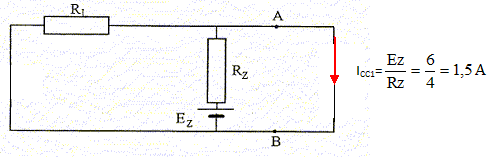

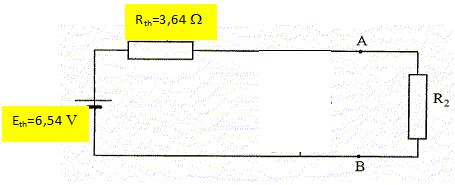On enlève Ez ; on note I_CC2 l'intensité du courant traversant le fil AB. ( Rz est court-circuitée )

I_CC = I_CC1+I_CC2 = 1,5+0,3 = 1,8 A.
Fem du générateur équivalent de Thévenin : E_th =I_CC R_th=1,8 *3,636 =6,545 ~6,5 V.

Calculer la valeur de la résistance R₂ pour que l’intensité du courant I₂ qui parcourt cette résistance soit égale à 80 mA.
E_th =(R_th+R₂)I₂ ;
R_th+R₂ =E_th / I₂ ; R₂ =E_th / I₂ -R_th = 6,545 / 0,080 -3,636 = 78,18 ~78 W.
Calculer la valeur de la tension U_AB.
U_AB = R₂I₂ =78,18*0,080= 6,254 ~6,3 V.
A partir du montage de base, calculer l'intensité des courants dans les résistances R₁ et R₂.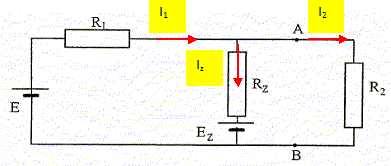

Loi des noeuds en A : I₁ = I₂ +Iz.
U_AB = R₂I₂ = E-R₁I₁ = Ez-R_zI_z =6,254 V
I₁ = (E- U_AB) / R₁ =(12-6,254) / 40 =0,1437 ~0,14 A.

Question 4 (5 points)

On observe à l'oscilloscope la tension u en créneaux ci-dessous, délivrée par un générateur :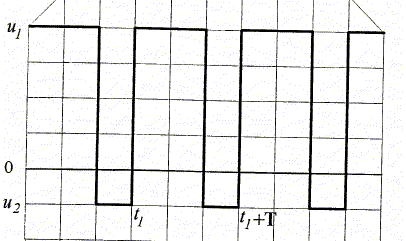

Echelle de temps : 1ms par division horizontale ;
Echelle de tension : 1 V par division verticale ;
- u₁ = + 4 V ;
- u₂ = - 1 V.
Donner les caractéristiques suivantes de cette tension :
− Période T : 3 divisions soit T = 3 ms = 3 10^-3 s.
− Fréquence F : 1/T = 1/ 3 10^-3 =333 Hz.
− Valeur moyenne de la tension en créneaux :
(2u₁ +u₂)/3 =(2*4-1) / 3=2,33 V.
− Valeur efficace de la tension en créneaux :

Ecrire l'équation d’une tension sinusoïdale qui aurait même fréquence et même valeur efficace.
u(t) = U_max sin(wt) avec U_max = U_eff *1,414 = 3,316*1,414 ~4,7 V.
et w = 2p F = 6,28*333,3 =2094 ~2,1 10³ rad/s.
Donner la valeur maximale de cette tension sinusoïdale.
U_max = U_eff *1,414 = 3,316*1,414 ~4,7 V.
Préciser si cette tension sinusoïdale aurait aussi la même valeur moyenne.
La valeur moyenne d'une tension sinusoïdale est nulle.

retour -menu