RLC dérivation, condensateurs, concours marine marchande filière professionnelle machine 2005.

. .

. .

Question 3 (6 points) Le montage ci-dessous est soumis à une tension VAB sinusoïdale de fréquence 50 Hz. 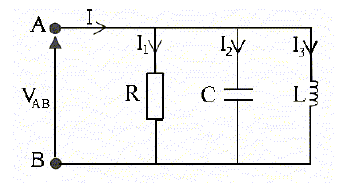On donne : VAB = 220 V ; R = 440 W ; C =5 µF ; l = 1 H. Calculer les valeurs des courants I1, I2 et I3 traversant respectivement la résistance R, le condensateur C et la bobine L. L'intensité efficace est égale à la tension efficace divisée par l'impédance de la branche. I1 = VAB / R = 220 / 440 = 0,50 A. I2 = VAB / Z2 avec Z2 =1/(Cw) et w = 2 pf = 2*3,14*50 = 314 rad/s. I2 = VABCw= 220*5 10-6*314 =0,3454 ~0,35 A. I3 = VAB / Z3 avec Z3 =Lw ; I3 = 220 / 314 =0,70 A. Déterminer la valeur du courant I, en utilisant la méthode de Fresnel. 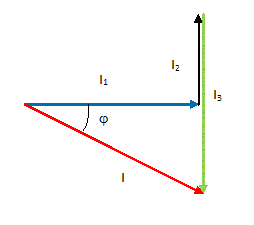I2 = I12 +(I3-I2)2 =0,52 +0,35462 =0,6157 ; I =0,6157½ =0,7847 ~0,78 A. En déduire le déphasage j entre le courant I et la tension VAB , ainsi que la valeur du facteur de puissance du montage. I1 est en phase avec VAB ; tan j = (I3-I2) / I1 =0,3546 / 0,5 = 0,709 ; j =35,34 ~35°. I est en retard de 35 ) sur VAB. le facteur de puissance cos f vaut : cos 35,34 =0,8157 ~0,82.   On veut remonter ce facteur de puissance à cos ϕ' = 0,9. Calculer la capacité du condensateur C1 qu'il faut monter en parallèle pour obtenir ce résultat. cos F' = 0,9 ; F' =25,84 ; tan 25,84 = 0,4843.  Les deux condensateurs C et C1, montés en parallèle, sont équivalents  à un condensateur unique C' traversé par l'intensité I'2. tan j' = (I3-I'2) / I1 ; I3-I'2 =I1 tan j' =0,5*0,4843 =0,2422 I'2 =I3-0,2422 =0,70-0,2422 =0,4578 A I'2 =VABC'w ;  C' = I'2 /(VABw )= 0,4578 /(220*314)=6,63 µF C' = C+C1 d'où C1 =6,63-5 = 1,63 µF ~1,6 µF. Question 4 (4 points) On réalise le montage représenté par la figure ci-dessous. Les deux condensateurs sont initialement déchargés. 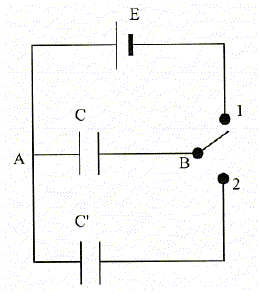On donne : E = 48 V ; C = 10 μF ;  C' = 5 μF. L'interrupteur est fermé en position 1. Déterminer à la fin du régime transitoire la tension aux bornes du condensateur C et calculer la charge de ce condensateur et son énergie E1. UAB = E = 48 V en fin de charge. Charge de l'armature A : Q = C UAB = 10-5*48 = 4,8 10-4 C. Energie stockée : E1 = ½CU2AB =0,5*10-5*482 = 1,152 10-2 ~1,2 10-2 J. On bascule l'interrupteur. Calculer la tension UAB aux bornes des condensateurs et la charge de chaque condensateur. On note q la charge finale de l'armature A du condensateur C et q' la charge finale de l'armature A du condensateur C'. La chage se conserve : Q = q + q'. de plus q = C UAB et q' = C'UAB. d'où Q = C UAB + C'UAB = (C+C') UAB. UAB.= Q/(C+C') = 4,8 10-4 / 15 10-6 = 32 V. q = 10-5 *32 =3,2 10-4 C. q' = 5 10-6 *32 =1,6 10-4 C. Calculer l'énergie E2 de l'ensemble des deux condensateurs ainsi chargés. E2 = ½CU2AB + ½C'U2AB =½(C+C')U2AB ; E2 = 0,5*15 10-6*322 =7,68 10-3 ~7,7 10-3 J.

retour -menu