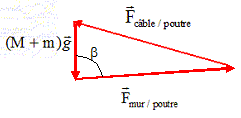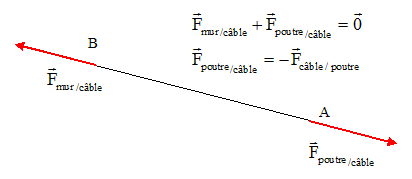équilibre d'une poutre, chute libre, concours marine marchande filière professionnelle machine 2005.

. .

. .

Question 1 (6 points) Un corps, dont le centre de gravité M est à la position O d'altitude h = 3 m par rapport au sol, est lancé verticalement vers le haut à l'instant t = 0, avec la vitesse initiale v0 = 4 m·s-1. Calculer la valeur de l'instant t1 où le corps atteint le point culminant M1 de sa trajectoire. Chute libre verticale avec vitesse initiale. On choisit un axe vertical orienté vers le haut, l'origine étant le sol. z = -½gt2+v0t+h z = -4,9 t2 +4 t + 3. La vitesse est la dérivée de la position par rapport au temps. v = -gt +v0 ; v = -9,81 t +4. L'altitude maximale est atteinte dès que la vitesse est nulle : d'où t1 = 4/9,81 =0,4077 ~ 0,41 s. Calculer l'altitude h' du point culminant. h' = -4,9t12+4t1+3 h' = -4,9 *0,40772 +4*0,4077 +3 =3,81~3,8 m. Calculer la valeur de l'instant t2 où le corps atteint le sol. z = 0 ; -4,9 t22 +4 t2 + 3= 0 discriminant : 16+4*3*4,9 =74,8 ; prendre la racine carrée : 74,8½ =8,6487 t2 = (-4-8,6487) / (-9,81) =1,2894 ~1,3 s. Calculer la vitesse à l'instant t2. v = -9,81 t2 +4. v = -9,81*1,2894 +4 = -8,649 ~ -8,6 m s-1. Le signe moins indique que le vecteur vitesse a le sens contraire de l'axe.   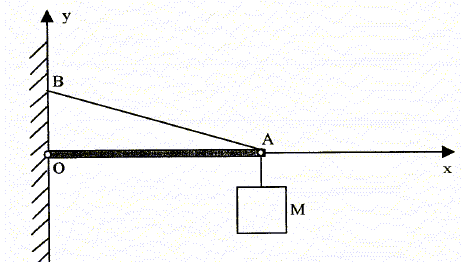Une poutre horizontale OA homogène de 3 m de longueur et de masse m = 40 kg est fixée à un mur par son extrémité O. Un câble AB de masse négligeable et inextensible de longueur 3,5 m relie le mur et l'extrémité A de la poutre. Une masse M = 150 kg est suspendue au point A de la poutre (voir figure ci-dessous). 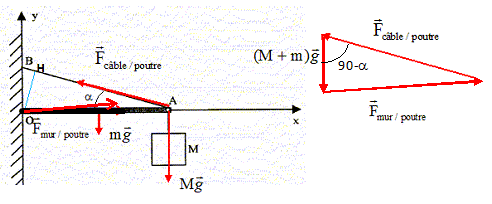On demande de déterminer dans le repère (O, x, y) les composantes des vecteurs représentant les forces suivantes : − la réaction du mur sur le câble ; − la réaction du mur sur la poutre. Equilibre de la poutre OA : La somme algébrique des moments des forces en O est nulle : - moment de la force mg, poids de la poutre ; bras de levier : ½OA ; rotation dans le sens horaire, compté positivement : +½OA mg ;  - moment de la force Mg appliquée en A ; bras de levier : OA ; rotation dans le sens horaire : +OA Mg ; - moment de la force F, appliquée en A ( action du câble sur la poutre ); bras de levier OH = OA sin a ; rotation dans le sens anti-horaire, compté négativement : -F OA sin a ; par suite : ½OA mg +OA Mg - F OA sin a avec cos a = OA/AB =3/3,5 =0,857 ; a = 31° F = (M+½m)g / sin a = (150 +0,5*40) *10 / sin 31 =3300,7 ~3,3 kN. composante horizontale : -3,3 * cos31 = -2,8 kN ; composante verticale : 3,3 * sin31 =1,7 kN. La somme vectorielle des forces appliquées à la poutre est nulle ; le triangle des force ci-dessus conduit  à :  F2mur / poutre = F2câble / poutre +[M+m)g]2-2 Fcâble / poutre * [M+m)g] cos (90-31 ) ;   F2mur / poutre =3300,72 +19002-2*3300,7*1900 cos 59 =8,0 106  ;  Fmur / poutre =(8,0 106)½ =2,836~2,8 kN. Calcul de l'angle ß :  F2câble / poutre = F2mur / poutre +[M+m)g]2-2 Fmur / poutre * [M+m)g] cos ß ;   3,302=2,842 +1,92-2*2,84*1,9 cos ß  ; cos ß =7,27 10-2 ; ß =85,8°. La force Fmur / poutre est inclinée de 4,2° sur l'horizontale. composante horizontale : 2,84 * cos 4,2 = 2,83 kN ; composante verticale : 2,84 * sin 4,2 =0,20 kN. Equilibre du câble : La liaison câble / mur cède lorsque sa composante horizontale est égale à 5 000 N. Calculer la charge maximale M' que peut supporter l'ensemble "poutre + câble" en A. F = (M+½m)g / sin a ; |composante horizontale| : Fx = F * cos a ; Fx =(M+½m)g / tan a ; Fx doit être inférieure  à 5 kN : (M'+½m)g / tan a < 5000 M'+½m < 5000 tan a  / g M' < 5000 tan a  / g -½m M' < 5000 tan 31/10 -20 M' < 280 kg M' < 2,8 102 kg.

retour -menu