Dipôle (RL), récepteurs en parallèle, concours marine marchande filière professionnelle machine 2006.

. .

. .

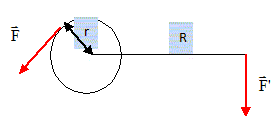
Question 1 (6 points) Un corps de masse 30 kg peut glisser sans frottement sur un plan incliné dont la pente est de 20 %. On l’immobilise en exerçant une force F  faisant un angle de 30° vers le haut avec le plan incliné. La force F est exercée au moyen d’un câble reliant le corps à un treuil dont le cylindre a un rayon de 10 cm, et la manivelle une longueur de 80 cm. On considère que l’accélération de la pesanteur vaut 10 N . kg-1. Représenter sur un schéma le corps, le treuil et les différentes forces qui s’exercent. 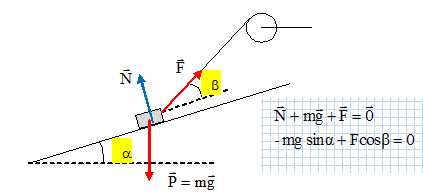Calculer l’intensité de la force F. F = mg sin a / cos ß avec sin a  = 0,20 (pente 20 % : le plan s'élève de 20 m  tous les 100 m parcourus ) F= 30*10*0,2 / cos 30 = 69,28 ~ 69 N.  Calculer l’intensité de la force F'qu’il faut appliquer, perpendiculairement à la manivelle. L'équilibre du treuil conduit à :  Fr = F' R. F' =Fr/R = 69,28*0,1/0,8 =8,66 ~8,7 N.   Calculer le nombre de tours de manivelle nécessaires pour monter le poids de 10 mètres sur le plan incliné. La corde s'enroule sur le cylindre de rayon r ; circonférence  : 2 p r. 2 p r n = 10 ; n = 10 /((2 p r) =10 /(2*3,14*0,1) =15,91 ~16 tours. Calculer alors le travail moteur réalisé en tournant la manivelle. 1 tour correspon à 2 p radians ; 15,91 tours corrspondent à q=15,91*2p = 99,96 radians. Travail de F' : W = F' R q = 8,66 *0,8*99,96 =692,5 ~6,9 102 J. En déduire la puissance fournie si le travail est réalisé en 24 secondes. Diviser le travail ( joule) par la durée (seconde). Puissance = 692/24 =28,8 ~29 W. Question 4 (4 points) On lâche sans vitesse initiale une pierre dans un puits, depuis son rebord et on entend le « flac » après un intervalle de temps de 3 secondes. On considère que la résistance de l’air est nulle, que le son a un mouvement de translation rectiligne uniforme et que l’accélération de la pesanteur vaut 10 m.s-2. Calculer le niveau de l’eau par rapport au rebord du puits, sachant que la vitesse du son est de 340 m.s-1. La pierre est en chute libre ; la distance parcourue est d = ½gt2. Durée de la chute : t =(2d/g)½. Durée de remontée du son : t' =d/340. Durée totale : t+t' = 3. (2d/g)½+d/340 =3 ; (2d/10)½+d/340 =3 ; (0,2d)½=3-d/340 ; élever au carré : 0,2 d = 9 + d2/3402-6d/340. Multiplier par 3402 : 0,2*3402d =9*3402+ d2-6*340 d. d2-2040d-23120d +1 040 400=0 d2-25160d +1 040 400=0 discriminant : 251602-4*1 040 400 =6,289 108. d =41,42 ~41 m. En déduire la vitesse d’impact de la pierre dans l’eau en km.h-1.  Dire si cette vitesse est fonction de la masse de la pierre.

retour -menu