Oscillateurs mécanique et électrique, géochronologie, concours EPF 2009.

. .

. .

Oscillateurs mécanique et électrique. On souhaite remplacer un oscillateur constitué d'une masse et d'un ressort par un circuit électrique de propriétés vibratoires équivalentes. On compare les propriétés vibratoires du système masse-ressors avec celles du système électrique LC idéal. 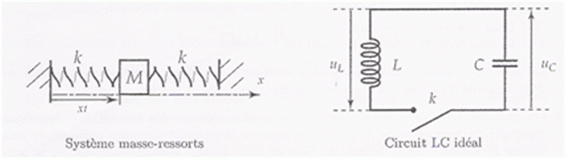Il n'y a aucune dissipation d'énergie dans  les deux dispositifs. En conséquence la résistance totale du circuit est supposée négligeable. les frottements du système masse-ressort sont négligeables. Etude du circuit LC. Etablir l'équation différentielle du circuit électrique vérifiée par la charge q du condensateur. additivité des tensions : uL+uC = 0. uL =Ldi/dt ; uC =q/C; i = dq/dt  ; di/dt =d2q/dt2 ; uL+uC = 0 s'écrit : Ld2q/dt2 +q/C =0 ; d2q/dt2 +q/(LC) =0. Donner la pulsation propre w0 et la période T des oscillations électriques. w20 = 1/(LC) ; w0 = 1/(LC)½ ; T0 = 2p /w0 =2p(LC)½. L'équation différentielle de caractéristique A est donnée par : A d2x/dt2 +x = 0. Montrer que x(t) = x0 cos (w0t) est solution de cette équation. Que représente x(t) pour le circuit LC ? Exprimer la constante A en fonction des paramètres L et C du circuit électrique. dériver deux fois par rapport au temps : x'(t) = - x0w0 sin (w0t)  ; x"(t) = - x0w20 cos (w0t)  = -w20 x(t) = -1/(LC) x(t). repport dans l'équation différentielle : -Aw20 x(t) + x(t) = 0 ; cette égalité est vérifiée quel que soit le temps  si Aw20 = 1 ; A = 1/ w20 =LC. x(t) correspond à la charge q.   Donner les expressions littérales de l'énergie magnétique de la bobine et de l'énergie du condensateur. Préciser les valeurs de ces énergies  à l'instant initial, lorsque l'interrupteur est fermé. Le condensateur est initialement chargé d'une énergie E0. Energie stockée par la bobine  à la date t : ½Li2  ;  énergie stockée par le condensateur à la date t : ½CuC2. Conservation de l'énergie : E0 = ½Li2 + ½CuC2. A l'instant initial le condensateur stocke toute l'énergie du dipole, c'est à dire E0. L'intensité initiale est nulle : la bobine ne stocke pas d'énergie  à la date t=0..   Etude du système masse-ressort. Ecrire l'énergie cinétique, l'énergie potentielle et l'énergie mécanique du système masse-ressorts. Energie cinétique : ½Mv2 ; énergie potentielle élastique : ½(2k) x2 ( l'origine est prise  à la position d'équilibre). L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle : EM= ½Mv2 +½(2k) x2 . Déterminer l'équation différentielle du mouvement en dérivant l'énergie mécanique par rapport au temps. L'énergie mécanique se conserve ; sa dérivée par rapport au temps est nulle. 0 = Mv v' +2k x x' avec v = x' et v' = x"  ; 0 = Mx' x" + 2k x x' simplifier par x' : 0 = Mx" +2k x. Montrer que cette équation est de la forme x" + 2Bx=0. Exprimer la constante B en fonction de la masse M et de la raideur des ressorts k. x" +2k/M x = 0 ; B = k/M. Analogie. Quelles conditions doivent être imposées pour avoir la même période dans le système mécanique et dans le système électrique ? La pulsation propre doit être la même : 2 B =2k/M = 1/(LC)  ; M = 2k LC. On impose la relation M= 1000 LC. Déterminer la valeur et l'unité de la raideur k d'un ressort. 1000 = 2k ; k = 500 N m-1. Géochronologie. Soit un isotope radioactif père (P) qui se désintègre en élément radiogénique fils (F). La quantité d'atomes P désintégrés dans le temps dt est proportionnelles au nombre P d'atomes et à la constante  de désintégration l. On peut écrire dP/dt = - l P (1) Définir les termes isotope et radioactif. Deux isotopes ont le même nombre de protons ( même numéro atomique ), mais des nombres de neutrons différents. Un noyau radioactif  est un noyau instable qui,par réaction nucléaire, conduit à un noyau plus stable, en libérant de l'énergie et en émettant  une particule a, ß ou g. Exemple de l'atome d'uranium 23892U. Ce noyau se transforme en un noyau de plomb 206 par une série de désintégrations successives dont on décrit les deux premières étapes : Dans la première étape, l'uranium 238 subit une radioactivité alpha. Le noyau fils est le thorium ( Th). Ecrire l'équation de la désintégration en précisant les règles utilisées. 23892U ---> 23490Th +42He. Conservation  de la charge : 92 = 90 +2. Conservation du nombre de nucléons : 238 = 234 +4. Dans la seconde étape, on a : 23490Th --> 23491Pa +0-1e. De quel type de radioactivité s'agit-il ? Justifier. Emission d'un électron : radioactivité de type ß-. On note P0 la quantité d'atomes pères à l'instant t=0. Intégrer l'équation (1) pour donner P(t), quantité d'atomes P à l'instant t, en fonction de P0, l et t ( équation 2). dP/dt = - l P  ; dP / p = - l dt ; d ln P = - l dt ; ln P = - l t + cste ; A t = 0 : ln P0 = cste ; ln P = - l t +  ln P0 ; P =  P0 exp(-l t). On souhaite dater un minéral dont la composition contient des atomes P. Connaissant la constante de désintégration l et sachant mesurer la quantité d'atomes présents, on pourrait utiliser l'équation 2 pour déterminer l'âge de cette roche. Malheureusement on se heurte  à un problème : on ne connaît pas le nombre d''atomes P0 présent à l'instant initial de formation du minéral. On pose alors l'hypothèse que le nombre d'atomes P(t) est égal aux nombre d'atomes P0 initiaux moins le nombre d'atomes fils radiogèniques produits au cours du temps t. Soit P(t) = P0 - F ou P0 = P+F (3). En combinant les équations 2 et 3, en déduire l'âge du minéral en fonction de l, P et F.  P0 = P exp(l t) ;   P exp(l t) = P + F ;  exp(l t) =1 +F/P ; l t = ln [ 1+F/P ]  ; t =1/ l   ln [ 1+F/P ]. Commenter cette méthode. Obtient-on ainsi avec certitude l'âge du minéral ? Cette méthode est précise dans la mesure où le noyau fils est stable et reste piégé dans le minéral. Certaines roches volcaniques contiennent du potassium ( symbole K) dont une partie est l'isotope 40( Z=19 ; A=40) qui se désintègre en calcium 40Ca et en un gaz inerte l'argon 40Ar (Z=18). La demi-vie du potassium 40 étant 1,25 109 ans, la datation sera basée sur la proportion, dans la roche, du potassium et de l'argon. Cette méthode permet de dater l'ensemble des 4,6 109 ans d'histoire de la terre.

retour -menu