QCM : dipôle LC, dipôle RLC, tension électrique, radioactivité : concours AVENIR. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Dipôle LC. 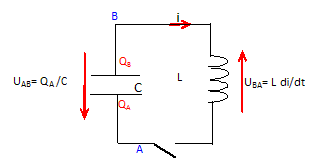la résistance de l'inductance est négligeable ; l = 20 mH t le condensateur a une capacité C = 50 µF. Le condensateur a été préalablement chargé ; on ferme l'interrupteur K  à l'instant t=0 et on note q(t) la charge de l'armature A . A t=0 la charge est positive et uAB=u0 = 12 V. L'énergie électromagnétique  à l'instant t vaut : E = ½Cq2 +½Li2. Faux. ½Cq2 n'a pas la dimension d'une énergie ; il faudrait écrire : ½q2/C. E = ½q2 /C + ½Li2. Faux. Il s'agit de l'énergie stockée  à la date t par le condensateur et la bobine : l'énergie électromagnétique est ½Li2. E = ½q2 /C + ½i2/L. Faux. ½i2/L n'a pas la dimension d'une énergie. E = ½Cq2 +½i2/L. Faux. On a l'égalité : E = ½Cu2 +½LC ( du/dt)2. Faux. u = q/C ; du/dt = 1/C dq/dt = i/C ; ( du/dt)2 = i2/C2 ; ½LC ( du/dt)2= ½L/C i2 ; ce terme n'a pas la dimension d'une énergie. E = ½Cu2 +½LC2 ( du/dt)2. Vrai. ½LC2 ( du/dt)2= ½L i2 ; E = ½u2 +½LC ( du/dt)2. Faux. les deux termes n'ont pas la dimension d'une énergie. E = ½Cu2 +½L2C2 ( du/dt)2. Faux. ½L2C2 ( du/dt)2= ½L2 i2 ; ce terme n'a pas la dimension d'une énergie. La conservation de l'énergie permet d'écrire l'équation différentielle : LC d2u/dt2 + u = 0. Vrai. E = ½Cu2 +½LC2 ( du/dt)2. dériver par rapport au temps : 0 =C u du/dt + LC2 du/dt d2u/dt2  ; simplifier par C du/dt : 0 = u + LC d2u/dt2  ; LC du/dt +½u du/dt=0. Faux. LCdu/dt + u = 0. Faux. L/C d2u/dt2 + u = 0. Faux. On en déduit alors :  um et j sont des constantes dépendant des conditions initiales u(t) = um cos[ t/ (LC)½ +j ] . Vrai. w2 = 1/(LC) ; w = 1/(LC)½ ; u(t) = um cos[ wt +j ]  ; t/ (LC)½ est en radian. u(t) = um cos[ t  (C/L)½ +j ]. Faux. u(t) = um exp(-t / (LC)). Faux. u(t) = um. Faux. En tenant compte des conditions initiales, on a alors : u(t) = 12 cos (100 t +½p). Faux. w = 1/(LC)½ =  1/(0,02*50 10-6)½ = 1000 rad/s. u(t) = 12 cos (1000 t ). Vrai. u(t=0 = 12 V. u(t) = 12 cos (100 t ). Faux. u(t) = 12 exp(-106t). Faux.   l'intensité  du courant i(t) est alors : i(t) = -6 sin (100 t ). Faux. la pulsation vaut 1000 rad/s.  i(t) = -0,6 sin (100 t ). Faux. i(t) = -0,6 sin (1000 t ). Vrai. i(t) = dq/dt = C du/dt = 50 10-6 *12 *1000 *(-1) sin (1000t) = -0,6 sin(1000t). i(t) = 60 exp(-106t). Faux. 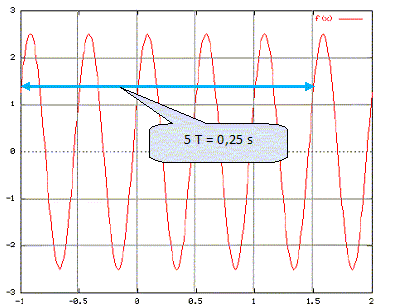Tension sinusoïdale : En abscisse, le temps est mesuré en dixièmes de secondes et en ordonnée la tension est en volts. La période T du signal est : (5 s ; 0,5 s ; 0,1 s ; aucune des 3 réponses précédentes) 0,25 / 5 = 0,05 s. La fréquence( en Hz) du signal est : (20 ; 200 ; 10 ; aucune des 3 réponses précédentes ) f = 1/T = 1/0,05 = 20 Hz. Le signal peut se mettre sous la forme V(t) = V0 sin (wt+j) avec : w = 40 p.  Vrai. w =2p f = 40 p rad/s. w = 40. Faux. w = 4p. Faux. w = 4. Faux. j =  p/6.  Vrai. V(t=0 ) ~1,3 V ; Vmax ~2,5 V ; 1,3 = 2,5 sin j ;  sin j ~0,5 ; j ~p/6 . j =  p/3. Faux. j =  p/2. Faux. j =  0. Faux. V0 = 5 V. Faux. V0 = 2,5 V. Vrai. V0 = 5 mV. Faux. aucune des trois réponses précédentes. Faux. Dipôle RLC. 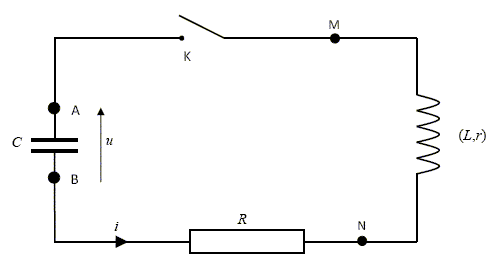Le condensateur étant chargé, on ferme l'interrupteur  à l'instant t=0. On a la relation ( interrupteur fermé ) uAB +uNB +uBM=0. Faux. additivité des tensions : uAB +uBN +uNM+uMA=0. La tension est nulle aux bornes d'un interupteur fermé : uMA=0 uAB +uBN +uNM=0. uAB + uMA + uNM + uNB = 0. Faux. uAB +  uNM + uBN = 0. Vrai. Aucune des 3 relations précédentes. Faux. On a la relation ( interrupteur fermé ) uNB =Ri.  Faux. uBN =Ri. Vrai. uNM =ri. Faux. uNM =ri +Ldi/dt. aucune des trois relations précédentes. Faux. On a : uNM =ri +Ldi/dt.  Vrai. uMN =ri +Ldi/dt. Faux. uNM =ri -Ldi/dt. Faux. aucune des trois relations précédentes. Faux. On a : i = Cdu/dt.  Vrai. i = dqA/dt = CduAB/dt ; si q = qA : i = Cdq/dt =Cdu/dt i = -Cdu/dt.  Faux.  u = Cdi/dt.  Faux. aucune des trois relations précédentes. Faux.   On a l'équation différentielle : LCd2u/dt2+(R+r)du/dt +u=0. Faux. uAB +  uNM + uBN = 0 ; u + ri + Ldi/dt +Ri=0 ; i = dq/dt = Cdu/dt ; di/dt = Cd2u/dt2; u + (r+R)C du/dt +LC d2u/dt2 = 0. LCd2u/dt2- (R+r)du/dt +u=0. Faux. LCd2u/dt2+u=0. Faux. aucune des trois relations précédentes. Vrai. Lorsque R=r=0, on a : des oscillations amorties. Faux. l'amortissement est du à la présence de résistances. des oscillations harmoniques. Vrai. des oscillations amplifiées. Faux. aucune des trois relations précédentes. Faux. Radioactivité. On considère une population formée de noyaux radioactifs tous identiques. On note N(t) la population à l’instant t et N0 la population à l’instant t = 0. On note l la constante de radioactivité caractéristique du type de noyau. dN/dt = -l N(t). Vrai. dN/dt  -l N(t)=0. Faux. N(t) = exp(-lt). Faux. N(t) =N0 exp(-lt). aucune des 3 réponses précédentes. Faux. On note t½ la demi-vie du type de noyau. t½ = 2 / l. Faux. t½ = ln2 / l. Vrai. N(t½) = 2 N0. Faux. N(t½) = ½ N0. aucune des 3 réponses précédentes. Faux. N(3t½) = 0,5 N0. Faux. N(t½) = ½ N0 ; N(2t½) = 0,25 N0 ; N(3t½) = 0,125 N0. N(3t½) = N0 /8. Vrai. N(3t½) = N0 /6. Faux. aucune des 3 réponses précédentes. Faux.

retour -menu