Moteur électrique triphasé, champ tournant, capesa 2010. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

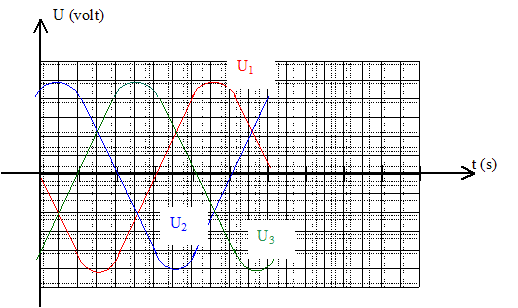
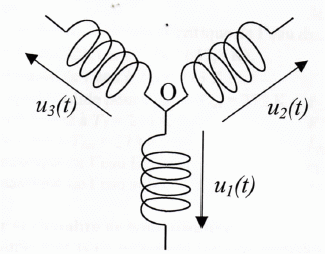
Une alimentation triphasée est caractérisée par trois tensions sinusoïdales de même valeur efficace U, de même fréquence f, mais déphasées  chacune de 120 ° par rapport  à l'autre. On les notera u1(t), u2(t) et u3(t), telles que : u1(t) = 2½U cos ( 2pft) u2(t) = 2½U cos ( 2pft-2p/3) u3(t) = 2½U cos ( 2pft+2p/3) Représenter l'aspect des trois courbes u1(t), u2(t), u3(t). On considère une bobine, d'axe de révolution Ox, parcourue par un courant i(t). 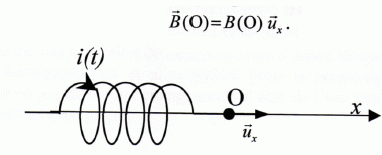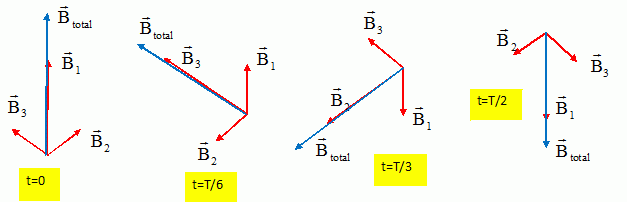Montrer par des considérations de symétrie que le champ magnétique crée par la bobine en O, est selon cet axe :   Le plan de la spire est plan de symétrie ; tout plan contenant l'axe de la spire est plan d'antisymétrie ;  le système invariant par rotation autour de l'axe.l'axe du système est axe de symétrie ;   Le champ magnétique est contenu dans un plan d'antisymétrie, perpendiculaire à un plan de symétrie de la distribution de courant. Trois bobines identiques sont positionnées dans un même plan avec leur axe situé à 120 ° l'un de l'autre. Elles constituent le stator d'un moteur de TGV. Le point commun O, qui relie les trois bobinages, est situé à égale distance de chaque bobine. On alimente chaque bobine par l'une des trois tensions triphasées. On note B1(t), B2(t) et B3(t) les intensités des champs magnétiques crées en O respectivement par u1(t), u2(t) et u3(t). B1(t) = B0 cos ( 2pft) B2(t) = B0 cos ( 2pft-2p/3) B3(t) = B0 cos ( 2pft+2p/3) On admet que le système des trois bobines crée en O un champ résultant constitué par la somme des trois champs associés à chacune des bobines. Montrer que ce champ résultant est un champ tournant à la fréquence des tensions sinusoïdales. En déterminer l'intensité en fonction de B0. Calcul fait pour wt compris entre 0 et p/6) : On choisit le repère (xOy) : Ox horizontal orienté  à droite, Oy vertical orienté vers le haut. Btotal  Ox = - [ B0 cos ( 2pft-2p/3) cos 30 - B0 cos ( 2pft+2p/3) cos 30] Btotal  Ox = - [ 2B0 sin ( 2pft) sin(2p/3) cos 30 ] = -1,5B0 sin ( 2pft). Btotal Oy =B0 cos ( 2pft) -[ B0 cos ( 2pft-2p/3) sin 30 + B0 cos ( 2pft+2p/3) sin 30 ] Btotal Oy =B0 cos ( 2pft) -[ 0,5B0 [ cos ( 2pft-2p/3) + cos ( 2pft+2p/3)]] Btotal Oy =B0 cos ( 2pft) - 0,5B0 [ 2cos ( 2pft) cos ( -2p/3)] Btotal Oy =B0 cos ( 2pft) - B0 cos ( 2pft) cos ( -2p/3)] = 1,5B0 cos ( 2pft). L'intensité du champ tournant est constante et vaut : 1,5 B0. 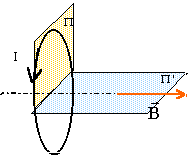Expliquer succinctement comment un rotor conducteur peut se mettre à tourner sous l'action de ce champ tournant. Toute pièce métallique soumise à une variation de flux est le siège de courant de Foucault ( induits ). Ces courants créent à leur tour un champ magnétique opposé au champ tournant ( loi de Lenz). L'intéraction des deux champs donne donc naissance à un mouvement de rotation du disque, à une vitesse inférieure à celle du champ tournant.

retour -menu