On
se propose dans cet exercice de déterminer les valeurs des grandeurs
caractéristiques d'une bobine (résistance r et inductance L) par deux
méthodes expérimentales différentes.
1.
Première méthode.
Deux séries de mesure sont réalisées, l'une en courant continu, l'autre
en courant alternatif sinusoïdal.
Mesures
en courant continu.
La
bobine est alimentée par un générateur délivrant une tension continue.
Un voltmètre et un ampèremètre, utilisés en mode DC, sont ajoutés dans
le circuit afin de pouvoir mesurer la tension aux bornes de la bobine
ainsi que l'intensité du courant qui la traverse.
Faire
un schéma du montage en précisant le sens de branchement des appareils.
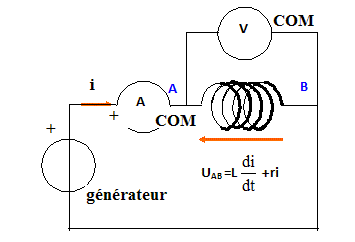
On lit sur les appareils de mesure les indications : U = 24,0 V ; I =
1,09 A
Comment
se comporte une bobine en régime continu ? Déterminer, avec un nombre
correct de chiffres significatifs, la valeur de la résistance r de la
bobine.
L'intensité est constante en courant continu : di/dt =0 ; la bobine se
comporte comme un conducteurohmique.
uAB = r i ; r =uAB / i
= 24,0 / 1,09 =22,02 ~ 22,0 ohms.
|
Mesures en courant
alternatif sinusoïdal
Le
générateur délivre à présent une tension sinusoïdale de valeur
efficace U' = 24,0 V et de fréquence f = 50,0 Hz.
Indiquer
le mode utilisé pour les deux appareils de mesure,
afin de pouvoir mesurer
les valeurs efficaces des grandeurs électriques.
Les appareils sont utilisés en mode AC.
|
.On lit sur les
appareils de mesure les indications : U' = 24,0 V ; I' = 558 mA
Déterminer
la valeur de l'impédance de la bobine.
Z
= U' / I' = 24,0 / 0,558 =43,01 ~ 43,0 ohms.
Rappeler
l'expression de l'impédance d'une bobine soumise à une tension
sinusoïdale en fonction de ses caractéristiques (r et L) et de la
pulsation ω.
Montrer
que l'inductance de cette bobine vaut : L = 0,118 H.
Z
= (r2 +(Lw)2
)½.
Z2 - r2
= (Lw)2
; L = (Z2 - r2
)½ / w avec w = 2 *3,14 f =
2*3,14*50 = 314 rad/s.
L= (432 -222)½
/ 314 =
0,118 H.
Afin de vérifier
ces résultats, on ajoute en série dans le circuit un conducteur ohmique
de résistance R'. La résistance totale du circuit vaut maintenant RT
= r + R' = 51,0 Ω. Un oscilloscope permet d'observer en voie A la
tension aux bornes du générateur et en voie B la tension aux bornes du
conducteur de résistance R', signal proportionnel à l'intensité.
On obtient l'oscillogramme ci-dessous avec un balayage de 2 ms/div :
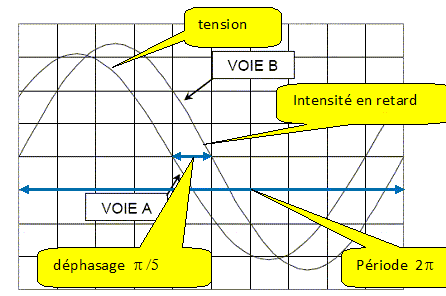
Déterminer
le déphasage ϕu/i de la tension u(t) aux bornes du générateur par
rapport à l’intensité i(t). Préciser et justifier son signe.
Lorsque
les deux courbes varient dans le même sens : la première qui passe par
un maximum est en avance sur l'autre ; la première qui s'annule est en
avance sur l'autre.
La
tension aux bornes du générateur est en avance sur l'intensité : cette
avance correspond à une division, alors que la période
correspond
à 10 divisions.
Un période correspond à 2 p radians ; Fu/i = + p/5 rad.
À partir
de cette valeur du déphasage ϕu/i, retrouver la valeur de l’inductance L.
tan
p/5= Lw / RT ; L = RT
tan p/5 / w
= 51,0 tan p/5 / 314 = 0,118 H.
Deuxième
méthode.
La bobine est maintenant placée en série avec un condensateur de
capacité C = 8,00 μF et un ampèremètre. L'ensemble est alimenté par un
générateur délivrant une tension sinusoïdale de valeur efficace U0
= 5,00 V. On fait varier la fréquence. On constate alors que
l'intensité efficace du courant passe par une valeur maximale I0
= 224 mA pour une fréquence f0 = 165 Hz.
Donner
le nom du phénomène mis en jeu.
Résonance d'intensité.
Déterminer, à
partir de ces valeurs :
La
valeur de l’impédance Z0 du dipôle
r, L, C série à la fréquence f0. Préciser
à quoi elle correspond. En déduire la résistance r de la bobine.
A la résonance d'intensité, l'impédance Z0 est
minimale, égale à la résistance r du dipole.
Z0
= r = U0/I0 =
5,00 / 0,224 =22,3
ohms.
La
valeur de son inductance L.
A
la résonance LCw02=1 avec
w0
= 2pf0
=2*3,14*165 = 1036,2 rad/s.
L = 1/ (Cw02)=1/(8 10-6*1036,22)
=0,116
H.
Utilisation
de la caractéristique d'une diode réelle.
On
souhaite déterminer l'allure de l'intensité i(t) du courant électrique
dans un circuit comportant une diode. Ce circuit est composé de trois
dipôles en série :
- un générateur G (considéré comme parfait)
délivrant une tension alternative en créneaux e(t) dont le tracé est
fourni ci-dessous ;
- un conducteur ohmique de résistance R = 8,0 Ω ;
- une diode réelle dont la caractéristique est fournie.
Le schéma du circuit est le suivant : 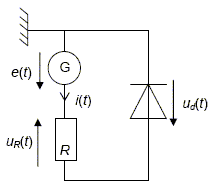
La diode idéale.
Tracer, sur la copie, l'allure de la caractéristique i = f(ud) d'une diode idéale.
Donner la valeur de ud lorsque la diode idéale est passante.
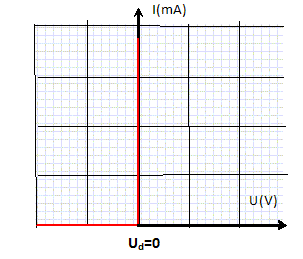
La tension est nulle aux bornes d'une diode idéale passante.
Comment évolue cette valeur de ud
si l'on considère la diode réelle (on ne demande pas de valeur précise)
? Justifier, à l’aide de la caractéristique de la diode fournie.
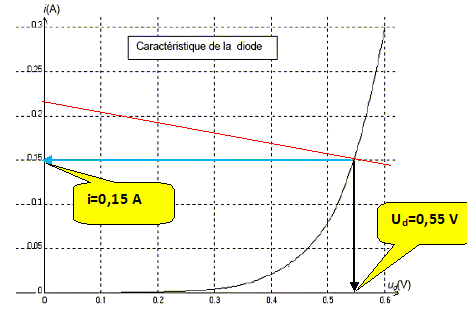
La diode réelle devient passante lorsque Ud est supérieure à 0,3 V. Puis Ud augmente avec l'intensité.
Étude du circuit.
Donner la relation entre les tensions e(t), ud(t) et uR(t), en précisant la loi utilisée.
Additivité des tensions dans un circuit série : e(t)= ud(t) + uR(t).
En déduire l'expression de ud(t) en fonction de e(t), i(t) et R.
uR(t) = R i(t) ; ud(t) =e(t) -R i(t).
Étude du circuit lorsque la tension e(t) est négative (t compris entre 50 ms et 100 ms)
Préciser si la diode est passante ou bloquée.
En déduire la valeur de l'intensité du courant pendant cette durée
L'intensité qui traverse la diode est nulle : la diode est bloquée.
En déduire la valeur numérique de ud.
ud(t) =e(t) -R i(t) avec i(t) = 0 ; donc ud(t) =e(t).
|
Étude du circuit lorsque la tension e(t) est positive (t compris entre 0 ms et 50 ms ou bien t compris entre 100 ms et 150 ms)
Préciser si la diode est passante ou bloquée.
Si Ud < 0,22 V, l'intensité qui traverse la diode est nulle : la diode est bloquée.
Si Ud > 0,22 V, l'intensité qui traverse la diode n'est pas nulle : la diode est passante.
Démontrer que l'intensité du courant peut se mettre sous la forme :
i = − 0,125 × ud + 0,219, avec i en A et ud en V
ud(t) =e(t) -R i(t) ; i(t) = [e(t)-ud(t) ] / R.
e(t)= 1,75 V ; R = 8,0 Ω ;
i(t) = [ 1,75-ud(t) ] / 8 ; i(t) = 0,219 -0,125 ud(t).
Tracer la courbe i = f(ud), appelée droite de charge, sur le même graphique que celui de la caractéristique de la diode.
En déduire graphiquement la valeur de l'intensité du courant dans le circuit lorsque le générateur fournit une tension positive.
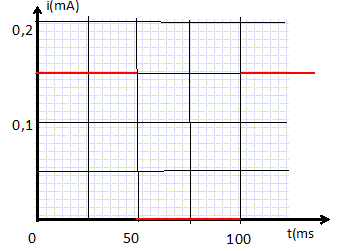
Représenter l'intensité i(t) du courant dans le circuit.
|
|
|