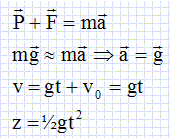L'huile dans l'eau, ça fait des vagues : bac S Polynésie 09 /2010 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

L’huile et l’eau sont deux liquides non miscibles. Lorsqu’on les verse l’un sur l’autre, et de n’importe quelle manière, on constate inexorablement que l’huile surnage sur l’eau. La masse volumique de l’huile est ρH = 800 kg.m-3 et la masse volumique de l’eau est ρE = 1,00.103 kg.m-3. Un élève réalise l’expérience suivante : à la date t = 0 s, il lâche une goutte d’huile de volume V = 0,50 mL, d’une hauteur H = 1,0 m au-dessus d’une cuve à ondes contenant de l’eau. On place une règle de 30 cm sur la surface de l’eau. Lorsque la goutte est dans l’air, il considère que les frottements sont négligeables. Masse volumique de l’air ρ = 1,30 kg.m-3. 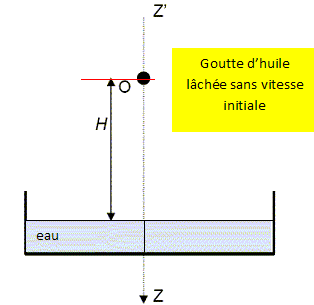Chute dans l’air.  Faire le bilan des forces agissant sur la goutte d’huile en mouvement dans l’air dans les conditions fixées en introduction et calculer leurs valeurs. On prendra g = 10 m.s-2. La goutte est soumise  à : - son poids, verticale vers le bas, valeur P = mg = ρH Vg  =800*5,0 10-7 *10 =4,0 10-3 N. - la poussée d'Archimède, verticale, vers le haut, valeur F = ρ Vg  =1,3*5,0 10-7 *10 =6,5 10-6 N. Montrer que l’on peut négliger une force par rapport à l’autre et indiquer laquelle. La poussée d'Archimède est négligeable devant le poids. Sur l’axe Z’Z, on fait coïncider l’origine O avec la position de la goutte juste au moment du lâcher. En appliquant la deuxième loi de Newton, déterminer la valeur de l’accélération de la goutte et établir l’équation horaire de son mouvement.   Utiliser cette équation horaire pour calculer la vitesse de la goutte d’huile lorsqu’elle frappe la surface de l’eau. H = 0,5 gt2 d'où t = (2H/g)½ ; v = gt = (2Hg)½ =(20)½ =4,47 ~4,5 m/s. Des ondes à la surface de l’eau. 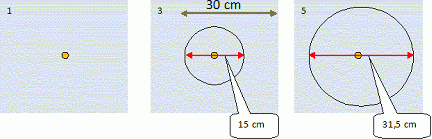Lorsque la goutte d’huile arrive dans l’eau, elle crée une déformation de la surface avant de s’étaler. Avec une caméra (webcam), on filme les ondes à la surface de l’eau. La caméra a enregistré le film à 10 images par seconde. On reproduit ci-dessous l’image n°1 réalisée à l’instant t0 = 0 s correspondant au contact de la goutte d’huile avec l’eau. Les troisième et cinquième images du film (image n°3 et image n°5) sont également représentées ci-dessous. Document en vue de dessus. Le cercle noir représente le front d’onde. Qu'appelle-t-on onde ? On appelle onde mécanique progressive le phénomène de propagation d'une perturbation dans un milieu matériel sans transport de matière, mais avec transport d'énergie. Une onde se propage, à partir de la source, dans toutes les directions qui lui sont offertes. Les ondes qui apparaissent sur la surface de l’eau sont-elles transversales ou longitudinales ? Justifier. Une onde est transversale lorsque le déplacement des points du milieu de propagation s'effectue perpendiculairement à la direction de propagation. Onde transversale à la surface de l'eau : chaque point P de la surface se soulève verticalement puis reprend sa place alors que les rides se déplacent horizontalement à la surface de l'eau. À l’aide des données expérimentales, calculer la vitesse de propagation des ondes à la surface de l’eau. D'après les photos n°3 et n°5, l'onde parcourt (31,5-15) / 2 = 8,2 cm =0,082 m. 10 images par seconde : la durée séparant deux images est donc 0,10 s ; la durée séparant la prise des images 3 et 5 est : 0,20 s. Vitesse de propagation de l'onde : v = 0,082 / 0,20  ~0,41 m/s. Des ondes en continu. 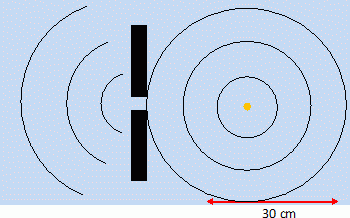On fait maintenant tomber, à intervalles de temps réguliers à l’aide d’un dispositif approprié, les gouttes d’huile sur la cuve à onde. À un instant donné, la surface de la cuve présente l’aspect suivant : 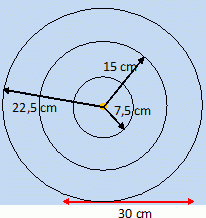Déterminer la distance entre les différents cercles noirs. Que représente-t'elle ? La longueur d'onde vaut l ~7,5 cm. En considérant que la vitesse de propagation des ondes est V = 0,38 m.s-1 à la surface de l’eau, calculer la fréquence à laquelle les gouttes d’huile tombent à la surface de l’eau. fréquence f = V / l  = 0,38 / 0,075 ~ 5,1 Hz. On interpose maintenant sur le trajet des ondes produites un obstacle qui présente une ouverture de 3 cm de large. Quel phénomène va-t-on observer ? Pourquoi ? Dessiner  la forme des ondes obtenues. La largeur de la fente dans l'obstacle est du même ordre de grandeur que la longueur d'onde : on observe le phénomène de diffraction.

menu