Histoires de pêche : bac S centre étrangers 2010 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

Le casting ou lancer de compétition est un epreuve de pêche qui consiste pour le compétiteur à lancer sa ligne aussi loin et aussi précisément que possible. Cette technique consiste à lancer un plomb d'une centaine de grammes à l'aide d'une canne et d'un moulinet. Le record de France, établi pour un plomb de 150 g est de 263,01 m. Lors de son passage à la verticale du pécheur, le plomb est à une altitude h = 6,00 m et possède une vitesse vH faisant un angle a avec l'horizontale. Le mouvement du plomb, objet sphérique, s'effectue dans le champ de pesanteur uniforme. g = 9,81 m s-2 ; masse du plomb m = 0,150 kg ; vitesse initiale vH = 44,4 m/s ; a = 50,0° ; masse volumique de l'air rair = 1,3 kg m-3 ; volume du plomb V = 1,5 10-5 m3. Etude du mouvement du plomb après passage à la verticale du pêcheur. Le système étudié est le plomb. Dans cette phase du mouvement,  la tension du fil sera négligée par rapport aux autres forces. On se propose, en situation de compétition, de déterminer les caractéristiques ( vitesse, accélération, position ) du plomb lors de son arrivée au sol. Les frottements de l'air sur le plomb sont négligés. 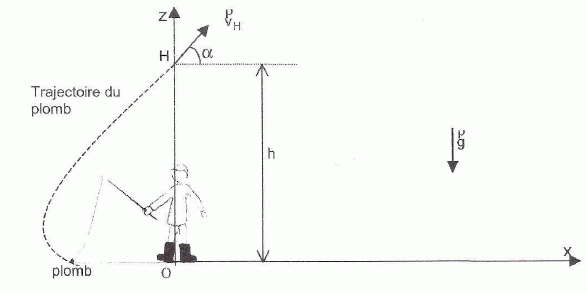Donner les caractéristiques ( direction, sens et expression littérale permettant de calculer leur valeur ) du poids P et de la poussée d'Archimède PA. Poids : verticale, ver le bas, valeur mg. Poussée d'Archimède : verticale, vers le haut, valeur ( poids du volume d'air déplacé )  rairVg. Peut-on négliger la poussée d'Archimède par rapport au poids ? Justifier. mg = 0,150*9,81 = 1,47 N rairVg = 1,3 * 1,5 10-5 *9,81 = 1,9 10-4 N. La poussée est négligeable devant le poids.   Détermination de la vitesse du plomb lorsqu'il arrive au sol. Le plomb est assimilé dans la suite du sujet à un objet ponctuel. Le choix des états de référence est tel que : l'énergie potentielle de pesanteur Epp est nulle au niveau du sol. Exprimer l'énergie potentielle de pesanteur Epp(H) du plomb lors de son passage à la verticale du pêcheur. Epp(H) = m h g. Exprimer l'énergie cinétique Ec(H) du plomb lors de son passage à la verticale du pêcheur. Ec(H) = ½mvH2. Donner l'expression de l'énergie mécanique Em(H) du plomb lorsqu'il passe à l'altitude h. Em(H) = Ec(H) + Epp(H) = ½mvH2 + m h g. Dans le cadre d'une chute libre, utiliser la conservation de l'énergie mécanique pour montrer que la vitesse du plomb a pour expression vS = (2gh+vH2)½ lorsqu'il touche le sol. Calculer sa valeur. Au sol l'énergie potentielle de pesanteur est nulle ; l'énergie mécanique est donc sous forme d'énergie cinétique : Em(sol) = Ec(sol)= ½mvS2 ; En l'absence de frottement, seul le poids travaille et l'énergie mécanique reste constante : Em(H) =Em(sol) ½mvH2 + m h g = ½mvS2 ; vH2 + 2 h g = vS2 ; vS = (2gh+vH2)½. vS = (2*9,81*6 + 44,42)½ = 45,7 m /s. En appliquant la seconde loi de Newton dans le cadre de la chute libre, déterminer les coordonnées  du vecteur accélération et du vecteur vitesse du cetre d'inertie du plomb. L'origine des dates est repérée par l'insatnt de passage à la verticale du pêcheur. En déduire l'expression de la vitesse vt) du plomb. v(t) = [vx2 + vz2]½ = [vH2 cos2a+ (gt)2 +vH2 sin2a-2gtvH sin a]½ =[vH2 + (gt)2 -2g t vH sin a]½. Montrer que la durée de la chute satisfait à l'équation :  (gt)2 -2g t vH sin a -2gh = 0. vH2 + 2 h g = vS2 ; vH2 + 2 h g =vH2 + (gt)2 -2g t vH sin a 2 h g = (gt)2 -2g t vH sin a ; (gt)2 -2g t vH sin a -2gh = 0. gt2 -2 t vH sin a -2h = 0. Vérifier que la durée de la chute est 7,11 s. 9,81 t2  -2 *44,4 sin 50 t-2*6 = 0 ; 9,81 t2  -68,0 t-12 = 0 ; D = 682+4*9,91*12 =5095 ; D½ =71,4 t = (68+71,4 ) / (2*9,81) =7,11 s. Montrer que les équation horaires du mouvement s'expriment sous la forme : x(t) = vH t cos a ; z(t) = -½gt2 + vH t sin a +h. Le vecteur position est une primitive du vecteur vitesse. La position initiale est : xH = 0 ; zH = h. d'où x(t) = vH t cos a ; z(t) = -½gt2 + vH t sin a +h. En déduire la valeur de la distance xmax atteinte par le plomb dans les conditions du lancer. x(t) = vH t cos a avec t = 7,11 s. xmax = 44,4 *7,11 *cos 50 = 203 m. Déduire l'équation de la trajectoire du centre d'inertie du plomb à partir des équations horaires. t = x / (vH cos a); repport dans z(t) : z = -½g x2 / (vH cos a)2 + x tan a  + h. C'est une branche de parabole. En utilisant l'expression de l'équation de la trajectoire, indiquer les paramètres de lancement qui jouent un rôle dans le mouvement ultérieur du projectile. G est une constante ; h, a et vH jouent un rôle dans le mouvement du projectile.

menu