Mathématiques. annale zéro, DNB 2026. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . Exercice 1. 6 points. Question 1.   Quelle est la mesure, en degrés, d’un angle droit ? 90°. Question 2. Voici une série de quatre notes : 8, 10, 11, 11. Quelle est la moyenne de cette série ? (8 +10 +11 +11) / 4 =10.   Question 3. Dans un collège de 800 élèves, 25% des élèves portent des lunettes. Combien d’élèves portent des lunettes ? 800 x0,25 = 200. Question 4. 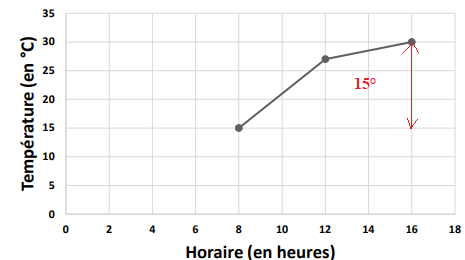Le graphique ci-dessous donne l’évolution de la température (en degrés Celsius) en fonction de l’horaire (en heures). Entre 8h et 16h, de combien de degrés la température a-t-elle augmenté ? Question 5. Une voiture roule à 90 km/h. Combien de temps met-elle pour parcourir 45 km ? 30 minutes ou 0,5 heure. Question 6. Donner le périmètre du losange ABCD de 3 cm de côté Les 4 côtés sont égaux : périmètre =3 x4 = 12 cm. Question 7 Pour résoudre l’équation 4x − 3 = 20 on effectue le calcul : 4x = 20 +3 = 23 ; x = 23 / 4. Question 8.   Sur la figure ci-dessous, les droites (DE) et (AC) sont parallèles. Écrire une égalité de rapports permettant de déterminer la longueur AB. 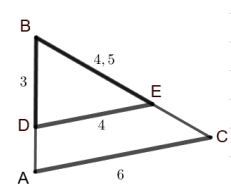Propriété de Thalès : AB / BD = BC /BE = AC / DE. AB = AC x BD / DE = 6 x3 / 4 =4,5. Question 9 On considère l’algorithme suivant : Quel résultat obtient-on si on choisit 1 comme nombre de départ ? 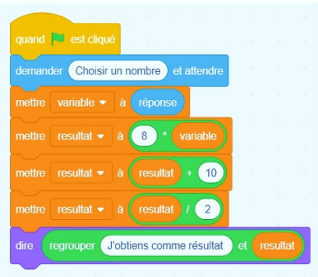8 x 1 =8. 8+10 = 18. 18 / 2 = 9. Exercice 1 : 3 points.    Sur la figure ci-dessous, les points B, A et D sont alignés. Les droites (BA) et (EC) sont parallèles. 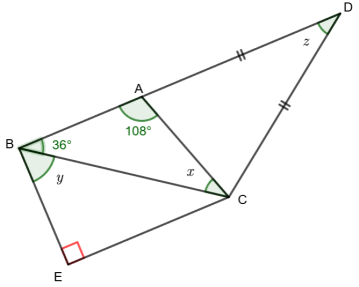1. Rappeler la propriété de la somme des angles d’un triangle, puis calculer la mesure de l’angle ACB repéré par la lettre x. La somme des angles d'un triangle est égale à 180 °. 108+36+x = 180 ; x = 180-36-108=36 °. 2. a. Que peut-on dire des droites (AB) et (EB) ? Justifier la réponse (AB) et (EC) sont parallèles ; (EC) et (BE) sont perpendiculaires. Donc (AB) et (BE) sont perpendiculaires. b. En déduire la mesure de l’angle CBE repéré par la lettre y. 36+y = 90 ; y = 90-36 =54 °. 3. On s’intéresse à l’angle ADC repéré par la lettre z. Déterminer la mesure de cet angle en expliquant chaque étape de la démarche. Le triangle ACD est isocèle. Mesure de l'angle CAD : 180-108 = 72°. L'angle z mesure : 180 -72 -72 =36°. Exercice 2 : 2 points.   Une urne contient 21 jetons numérotés de 1 à 21 indiscernables au toucher. On tire un jeton au hasard. 1. On note A l’événement « obtenir 2, 3 ou 10 ». Calculer la probabilité de l’événement A. On donnera le résultat sous forme de fraction irréductible. 3 cas favorables sur 21 possibles : 3 / 21 = 1 / 7. 2. a. On note B l’évènement « obtenir un jeton dont le numéro est un diviseur de 24». Donner les issues de l’évènement B. Diviseurs de 24 :1 ; 2 ; 3 ; 4 ; 6 ; 8 ; 12  b. Déterminer la probabilité de l’événement B. 7 cas favorables sur 21 possibles : 7 / 21 = 1 /3.. Exercice 3. 4,5 points.  Un paquet de lessive vide pèse 200 g. On y verse de la lessive. On sait que 1cm3 de lessive pèse 1,5 g. 1. Quelle est la masse totale d’un paquet de lessive (masse de la lessive et masse du paquet vide) contenant 1 600 cm3 de lessive ? Masse de lessive : 1600 x1,5 =2400 g. Masse totale : 200 + 2400 = 2600 g. 2. On considère la fonction f qui à x associe 1,5x + 200.  a. Lorsque x représente le volume de lessive en cm3, que représente la valeur f(x) ? f(x) représente la masse totale du paquet. b. Représenter graphiquement la fonction f dans un repère orthogonal. On placera l’origine du repère en bas à gauche sur une feuille de papier millimétré. Sur l’axe des abscisses on prendra 1 cm pour 200 cm³ et sur l’axe des ordonnées 1 cm pour 200 g.  3. a. En laissant les traits de construction apparents, trouver, par lecture graphique, le volume de lessive contenu dans un paquet de lessive de 2 300 g. b. Retrouver ce résultat par le calcul. 2300 = 200+1,5 x ; 1,5 x = 2100 ; x =2100 /1,5=1400 cm3..  c. Un paquet de lessive en forme de pavé de largeur 12 cm, de profondeur 8 cm et de hauteur 15 cm peut-il contenir un tel volume ? Argumenter la réponse en précisant la démarche. Volume du pavé : 12 x 8 x15=1440 cm3 > 1400 cm3. Réponse oui. Exercice 4 : 2,5 points Dans un collège, 91 filles et 77 garçons participent à un club sciences. On souhaite former des groupes, de sorte que chaque groupe ait le même nombre de filles et le même nombre de garçons. 1. Décomposer 91 et 77 en produit de facteurs premiers. 91 = 7 x 13 ; 77 = 7 x 11. 2. En déduire combien de groupes au maximum on peut former. Argumenter la réponse en précisant la démarche. Le nombre de groupes correspond au  PGDC(77 ; 91) = 7. 3. Dans ce cas combien d’élèves y aura-t-il dans chaque groupe ? 13 filles et 11 garçons soit 24 élèves.

menu