Suite positive et suite bornée, concours général mathématiques 2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Suite positive et suite bornée. Pour tout réel a, on appelle suite associée à a la suite (un) définie par u0 =u1 = 1 et un+2 = u2n+1 −au4n pour tout entier n > 0.  On dit que a vérifie la propriété P si tous les termes de la suite (un) assoctée à a sont strictement positifs, et que a vérifie la propriété B si la suite (un) associée à a est bornée. Partie 1 : Propriété P. 1. Quels sont les réels a qui vérifient la propriété P et qui appartiennent : a. à l’intervalle [1 ; +∞[ ? a > 1 et a vérifie la propriété P, donc  pour tout entier naturel n, un >0. u2 =  u21 −au40 =1-a >0. donc a < 1, ce qui est impossible. Quelque soit  a > 1 , a ne vérifie pas la propriété P. b. à l’intervalle ]−∞; 0] ? a < 0, donc -a > 0. un+2 = u2n+1 +(−a)u4n Démonstration par récurence. Initialisation : u0=u1 = 1  est vraie. Hérédité : u2n+1 >0 ; -a >0 ;- au4n >0 donc un+2>0. Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel n. a < 0 vérifie la propriété P. 2. Soit a un réel appartenant à l’intervalle ]0;1[ et (un) la suite qui lui est associée; on suppose, dans cette question, que a vérifie la propriété P. a. Démontrer que 0 < un+1 <un < 1 pour tout entier n >0. Démonstration par récurence. Initialisation : u0=u1 = 1   ; 0 < u0 < u1 < 1  est vraie. Hérédité :  a vérifie la propriété P, donc un >0 , un+1 >0 et un+2 >0. un+2 = u2n+1 −au4n . un+2-un+1=u2n+1 −au4n -un+1. 0 < un+1 < 1 donc u2n+1 < un+1. Par suite u2n+1 −au4n -un+1 < un+1 −au4n -un+1. un+2-un+1 <−au4n < 0. un+2 < un+1 < 1. L'hérédité est bien vérifiée. b. Quelle est la limite de la suite (un) ? La suite (un) est décroissante et minorée donc elle converge vers une limite l réelle comprise entre 0 et 1. A partir d'un certain rang : l = l2 -al4. -l2 +al4+l =0 ; l(1-l+al3)=0. l=0 ou 1-l+al3=0. Etude de f(x) = ax3-x+1 ; f '(x) = 3ax2-1. f '(x) = 0 si x = 1/(3a)½. f '(x) < 0 sur [0 ; 1/(3a)½[ et f(x) décroît de 1 à a appartenant à ]0;1[ . Donc 1-l+al3 diffère de 0 et l=0. c. Pour tout réel n > 0, on pose xn =un+1/u2n. . Exprimer xn+1 en fonction de a et de xn. 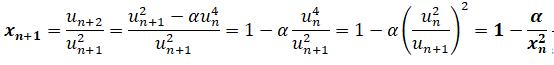d. Démontrer que la suite (xn) admet une limite finie, que l’on notera xoo et exprimer x2oo(1−xoo) en fonction de a. On va démontrer par récurrence que xn+1-xn < 0. Initialisation : x0 = 1 et x1 = 1-a ; x1-x0 < 0. Hérédité : xn+1-xn < 0 est supposé vrai. 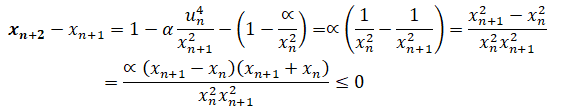La suite (xn) est donc décroissante et xn >0 ; donc la suite est minorée.  La suite converge vers xoo réel. Hypothèse : xoo =0+ : xoo = 1-a / x2oo =0 ; le terme de droite tendtait vers moins l'infini et le terme de gauche vers zéro. L'hypothèse est donc fausse. xoo = 1-a / x2oo ; a / x2oo =1-xoo ; a = x2oo(1−xoo). e. En déduire que a < 4 / 27. xn >0 ; x0=1 ; xn+1  < 1 ;  xn appartient à ]0 ; 1]. xoo appartient à ]0 ; 1]. xoo est solution de a = x2oo(1−xoo). -x3oo+x2oo-a=0. Etude de la fonction f(x) =- x3+x2-a. f '(x) = -3x2+2x =-x(3x-2). 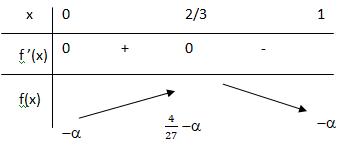On cherche au moins une solution dans [0 ; 1) de f(x) = 0. 4 / 27 -a >0 ; a < 4 / 27. 3. Quels sont les réels a qui vérifient la propriété P ? . ... .... .. =

menu