Fibre
optique et interférences, prisme et réflexion totale,
concours général
physique chimie 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Fibre optique et interférences.
Une
portion de longueur L = 2 cm de fibre optique monomode ( SMF) est
remplacée par une fibre à cristalphotonique ( PCF) permettant la
propagation de deux modes distincts. Chaque mode est associé à une
vitesse de propagation de la lumière dans la fibre. On note n1 ( coeur de la fibre) et n2 ( couronne entourant le coeur) les indices optiques de ces deux modes.
L'onde
lumineuse est supposée monochromatique de longueur d'onde l accordable
autour de lmoy=1,5 µm et provient du coeur de la fibre monomode et retourne
après la portion PCF dans une fibre monomode.
Dans le cadre de l'optique géométrique, la couronne ne devrait pas être
parcourue par une onde lumineuse qui reste confinée dans le coeur.
57. Identifier le phénomène responsable de la présence d'onde lumineuse dans la couronne.
La lumière incidente à l'interface coeur-couronne est fortement diffusée par les trous d'air.
Schématisation des deux chemins pris par chaque onde lumineuse.
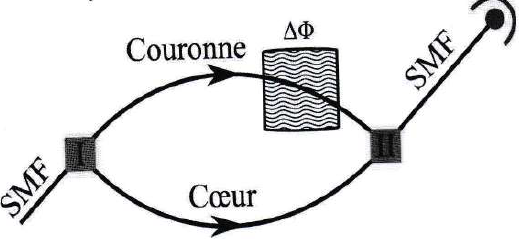
La différence de phase accumulée entre l'onde lumineuse passant par le coeur et celle passant par la couronne est notée
DF = 2 p /Dt où Dt correspond à la différence de temps du parcours des ondes dans chaque mode.
En sortie de fibre un détecteur permet de mesurer l'intensité lumineuse
selon la longueur d'onde. Celle-ci peut-être modélisée par :
I(l) = I1 +I2 +2(I1I2)½ cos ( DF).
I1 et I2 sont les intensités lumineuses de l'onde passant respectivement par le coeur et la couronne.
58. Justifier que la différence de phase caractérisant l'interférence observée en sortie de fibre est :
DF = 2p(n1-n2) L / l.
Diffrénce de marche : d=(n1-n2) L.
Différence de phase : DF = 2 p / l d.
DF = 2p(n1-n2) L / l.
59. Justifier que pour l = lmoy-dl où dl << lmoy l'intensité lumineuse puisse s'écrire :
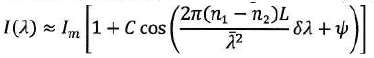
Y =2p(n1-n2)L / lmoy.
Donner l'expression de Im et de C en fonction de I1 et I2.
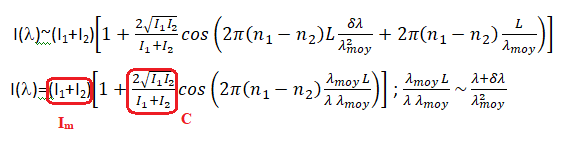
On suppose à partir de maintenant que lmoy =(n1-n2)L / k avec k entier relatif.
60. Simplifier l'expression de I(l).
Y =2kp.
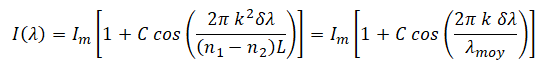
En présence d'ammoniac, l'indice optique de la couronne est modifié et vaut n2+dn avec d n << n2.
61. Justifier qu'en présence d'ammoniac, lmoy pour laquelle I(l) atteint son premier minimum est décalée de :
Dl = lmoy dn / (2k n1-n2).
62. Montrer que la variation d'indice optique dn dépend de Dl selon dn= 2k2Dl / L.
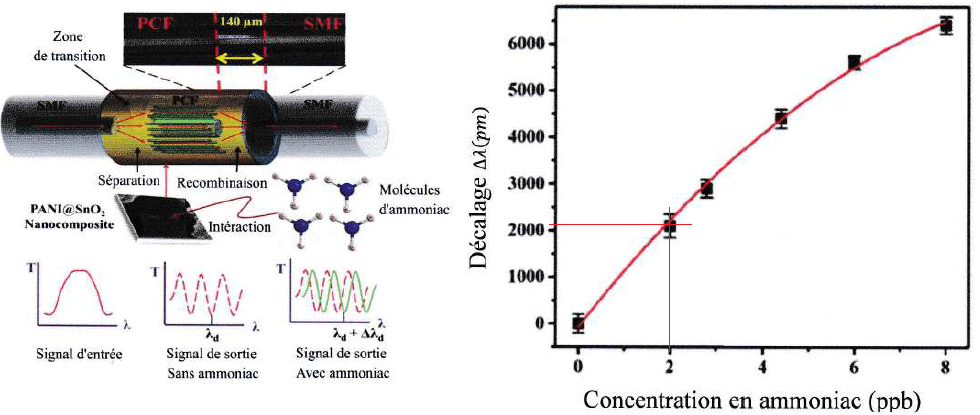
63. En supposant
que k ~1 estimer la variation d'indice optique détecté par cette
méthode lorsque la concentration d'ammoniac est de 2ppb soit Dl ~2000 pm. Commenter.
dn ~2 x2000 10-12 / 0,02 =2 10-7, valeur très faible.
Une très faible quantité d'ammoniac peut être détectée.
Pour des personnes en bonne santé, l'ammoniac est convertie en urée
dans le foie. L'urée est transportée via le flux sanguin et éliminée
danns l'urine par lre reins. Pour des personnes atteintes
d'insuffisance rénale chronique, l'urée accumulée est dégradée
par uréase salivaire en ammoniac qui se retrouve dans l'air
exhalé.
Pour des concentrations en ammoniac dans l'haleine supérieures à 1,6
ppm la personne est malade ( insuffisance rénale). La personne est en
bonne santé pour des concentrations inférieures à 1,1 ppm.
64. Comparer les
valeurs des concentrations en ammoniac détectable par cette
méthode et celles permettant de détecter une insuffisance rénale.
Conclure sur l'applicabilité de cette méthode à ce type de diagnostic.
2 ppb= 2 10-9 m ; 1,6 ppm = 1,6 10-6 m = 800 x 2 ppb.
dn=800 x2 10-7=1,6 10-4.
1,1 ppm = 1,1 10-6 m = 550 x 2 ppb.
dn=550 x2 10-7=1,1 10-4.
La variation d'indice est détectable ; le diagnostic est possible.
|
...
|
....
|
Prisme et réflexion totale.
On considère un rayon lumineux incident sur un dioptre séparant les milieux d'indice n1 et n2.
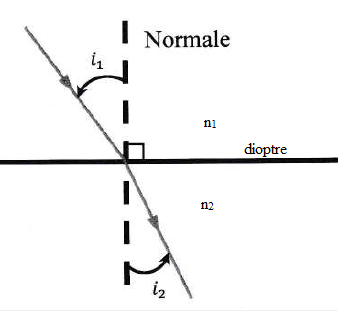
65. Rappeler la troisième loi de Snell-Descartes.
Rayons incident, réflchi et réfracté sont coplanaires.
n1 sin i1 = n2 sin i2.
Une fine couche d'or déposée à la surface d'un prisme peut transporter
une onde électromagnétique appelée plasmon de surface. En présence
d'une onde lumineuse incidente, celle-ci peut produire un tel plasmon
lors de sa réfraction à travers l'interface. Il est aisé de mettre en
évidence ce phénomène à condition de choisir un angle d'incidence tel
que :
i > ilim = sin-1(n2 /n1).
66. Donner la valeur de l'angle de réfraction i2 lorsque i1 = ilim.
i2 = p/2.
67. Expliquer le terme de "réflexion totale" caractérisant la situation i1 > ilim.
Le rayon réfracté n'existe plus. Le rayon incident est totalement réfléchi à l'interface.
La production d'un plasmon de surface modifie la troisième loi de Snell Descartes. Celle-ci devient :
n1 sin(i1)=n2 sin (i2) +n1 2p l1 / lp pour i1 > ilim. (4)
l1 = 0,63 µm. lp ~ 10 µm est la longueur d'onde du plasma de surface.
68. A partir de l'équation (4) expliquer pourquoi la présence d'un plasmon de surface permet d'obtenir un rayon réfracté même si i1 > ilim.
n1 sin(i1)=n2 sin (i2) +n1 2p *0,63 / 10.
n1 sin(i1)=n2 sin (i2) +0,126 n1.
n2 sin (i2)= n1 (sin(i1)-0,126) ;
sin (i2)= n1 / n2 (sin(i1)-0,126) ;
n1 / n2 > 1 et sin(i1)-0,126 < 1.
Donc n1 / n2 (sin(i1)-0,126) peut être inférieur ou égal à1 et le rayon réfracté existe.
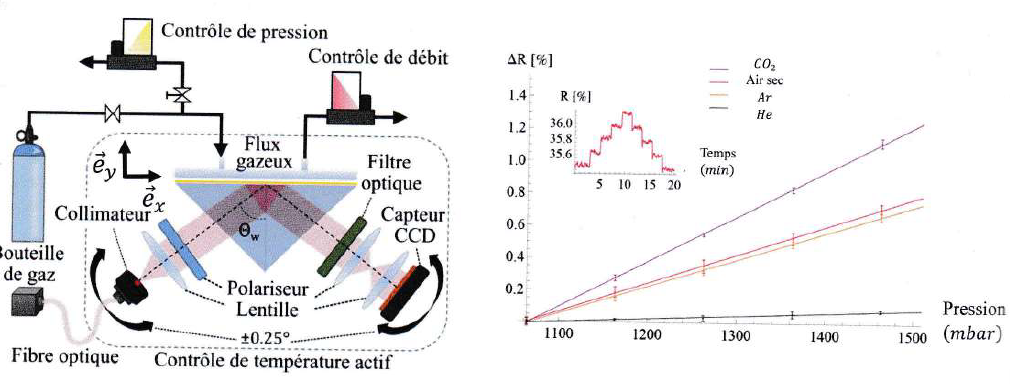
L'angle de travail qw est tel que qw >ilim.
L'intensité de l'onde lumineuse réfléchie à la surface du prisme est
mesurée par un capteur CCD après un filtre optique permettant de
sélectionner précisément la longueur d'onde. La variation de
réflectivité R ( grandeur proportionnelle à l'intensité de l'onde
réfléchie sur la base du prisme) pour différentes espèces chimiques et
pour différentes pressions partielles à la surface de la couche d'or
est représentée. En particulier l'insert de cette figure met en
évidence la variation mesurée en fonction du temps lorsque la pression
en molécule odorante est augmentée puis diminuée sur un intervalle de
temps d'une vingtaine de minutes.
69. Justifier la présence du filtre optique.
Le filtre optique transmet de manière sélective une partie du spectre optique et en rejette d'autres.
70. Expliquer en
quoi ce dispositif permet de supposer que la présence d'un gaz diminue
la probabilité d'excitation d'un plasmon de surface.
Lorsque la pression du gaz augmente, la variation de réflectivité
croît. L'intensité de l'onde réfléchie augmente et en conséquence,
l'intensité de l'onde réfracté diminue.
|
|
=
|
|