Exercice 1 11 points
Du haut de ses 210 m et 59 étages, la tour Montparnasse est le plus
grand gratte-ciel de la ville de Paris. Elle fera peau neuve d’ici peu
: jardins, façades végétalisées, panneaux photovoltaïques, nouveau
vitrage transparent et isolant.
La future tour devrait à la fois changer d’aspect et améliorer ses
performances énergétiques.
Cet exercice propose d’étudier, dans un premier temps, le mouvement
d’un des ascenseurs équipant la tour. Il portera ensuite sur deux des
mesures visant à améliorer les performances énergétiques du bâtiment.
1. Mouvement du grand
ascenseur
L’objectif de cette première partie est d’étudier le mouvement du plus
grand ascenseur de la tour, qui relie le rez-de-chaussée, pris comme
référence d’altitude, au 56
e étage. On étudie le mouvement,
dans le référentiel terrestre supposé galiléen, du centre d’inertie de
l’ascenseur dans le champ de pesanteur considéré comme uniforme. Le
point O confondu avec le centre de masse de l’ascenseur lorsqu’il se
situe au rez-de-chaussée sera pris comme origine d’un axe Oz orienté
positivement vers le haut.
Données :
- loi fondamentale de la statique des fluides : P
B-P
A
=
rg(z
A-z
B)
avec : P
A, P
B : pression du fluide en deux points
A et B (en P en pascal) ;
r :
masse volumique du fluide (en kg m
-3) ;
g ∶ intensité de la pesanteur (9,81 m s
-2) ;
z
A, z
B : altitude des points A et B (en m) ;
- masse molaire de l’air dans les conditions de l’expérience : M=28,98 g
/ mol.
- constante des gaz parfaits : R= 8,314 J mol
-1 K
-1.
- relation entre la température exprimée en kelvin et la température
exprimée en degré
Celsius : T(K) =
q(°C)
+ 273,15.
On se propose, dans un premier temps, de vérifier la hauteur parcourue
par l’ascenseur lors d’un trajet, à partir d’un suivi de la pression
atmosphérique réalisé grâce à un smartphone. On considère que l’air
suit le modèle du gaz parfait. Les mesures obtenues permettent de
tracer la courbe suivante.
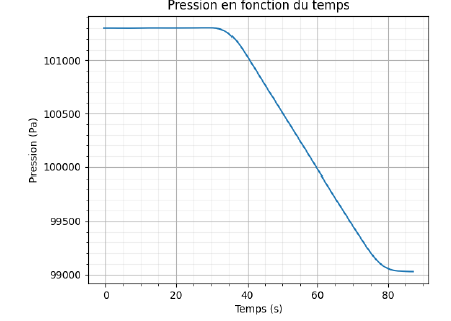 Q1.
Q1. À l’aide de la figure 1, justifier qualitativement que l’ascenseur monte lors de l’expérience.
A : point de départ et B point à l'altitude h.
La pression diminue au cours du temps ; PB-PA < 0.
zA-zB < 0 ; zB > zA.
L'ascenseur monte.
Q2. Exprimer l’équation d’état d’un gaz parfait, en précisant la signification et les unités des différentes grandeurs.
PV = n RT.
P pression en pascal; V : volume en m
3 ; n quantité de matière en mol ; T : température en kelvin.
R constante des gaz parfaits.
Le jour de l’expérience, la température était égale à 25,0 °C.
Q3. À l’aide de la
question précédente, montrer que la valeur de la masse volumique de
l’air au pied de la tour le jour de l’expérience est 1,184 kg m
-3.
P =101 300 Pa ; n = masse / M ; masse = V
rair ; n =
V rair / M ;
P = rair RT / M ; rair = P M / (RT) = 101 300 x28,98 10-3 /(8,314 x 298)=1,184 kg m-3.
Q4. Montrer que la hauteur h atteinte par l’ascenseur à la fin de son trajet est telle que :
h= (P
1-P
2) / (
rair g)
avec P1 et P
2 les pressions respectivement au pied et au sommet de la tour.
P1-P2=rairg(z2-z1)= rairgh.
h= (P1-P2) / (rair g)
Q5. Calculer la hauteur h atteinte par l’ascenseur à la fin du trajet. Commenter.
h = (101 300 -99 000) / (1,184 x9,81)=198 m, en accord avec la hauteur de la tour..
En plus de l’altitude finale de l’ascenseur, il peut être utile de
connaître son altitude au cours du trajet. Cette donnée permet
effectivement d’accéder à la vitesse de l’appareil, puis à son
accélération. Les différentes opérations utiles sont réalisées ici à
l’aide du programme en langage Python qui suit. Il contient, aux lignes
3 et 4, les 86 couples de valeurs (temps ; pression atmosphérique)
enregistrés par le smartphone lors de la montée.
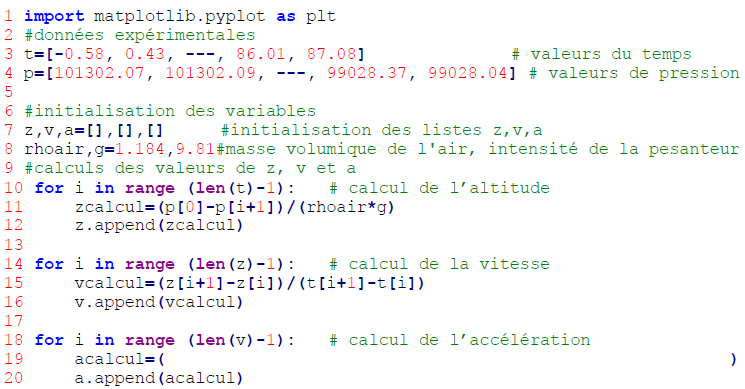 Q6.
Q6. Recopier puis compléter la ligne 19 du script Python ci-dessus pour calculer les valeurs de l’accélération.
acalcul=(vcalcul[i+1]-vcalcu[i]) / ( t[i+1]-t[i])
Q7. Indiquer, en justifiant, le nombre de valeurs de l’accélération calculées par le programme.
86 couples de valeurs enregistrées ; il faut deux valeurs de la vitesse
et deux valeurs du temps pour calculer une accélération.
(v
2-v
1) / (t
2-t
1) ; ....(v
i+1-v
i) / (t
i+1-t
i) ...
(v86-v85) / (t86-t85).
85 valeurs de l'accélération sont calculées.
La suite du programme permet de tracer les courbes
des figures 2 et 3, représentant l’évolution de la vitesse et de
l’accélération de l’ascenseur au cours du trajet étudié.
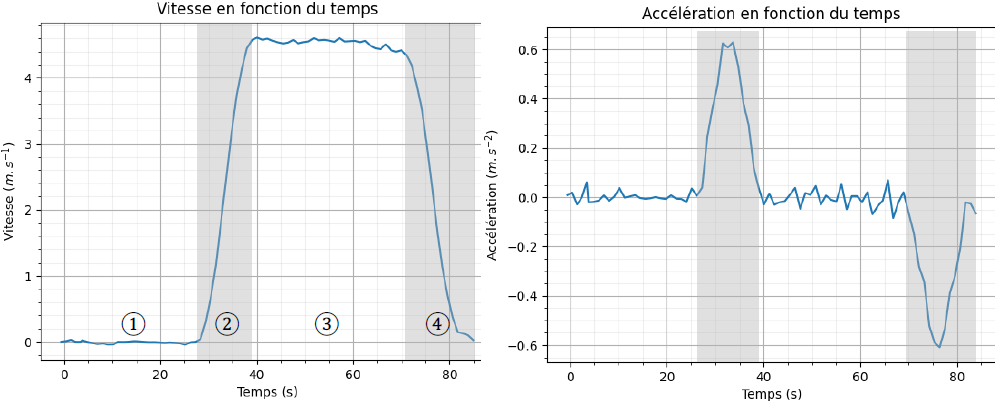 Q8.
Q8. Décrire le mouvement de
l’ascenseur dans le référentiel terrestre supposé galiléen lors des
quatre phases identifiées sur la figure 2.
1 : arrêt ; 2 : accélération ; 3 : montée à vitesse constante ; 4 : la vitesse diminue,décélération.
Q9. Justifier que la courbe d’accélération donnée en figure 3 est cohérente avec ces quatre phases.
1 :arrêt, accélération nulle ; 2 : la vitesse croît, accélération positive ;
3 : vitesse constante, accéllération nulle ; 4 : la vitesse décroît, accélération négative.
Les schémas ci-dessous représentent les forces s’exerçant sur
l’ascenseur,P correspondant au poids et F à l’ensemble des autres
forces verticales telles que la force élévatrice et les différentes
forces de frottement (air, freinage).
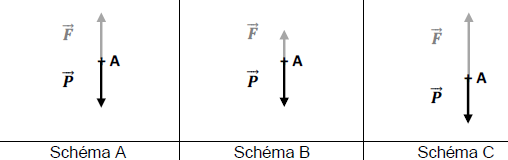 Q10.
Q10. Associer, en justifiant, un schéma à chaque phase du mouvement identifiée sur la figure 2.
Schéma A : les forces se compensent, accélération nulle :arrêt ou vitesse constante.( phases1 et 3).
Schéma B : P > F; accélération négative, la vitesse diminue. (phase 4).
Schéma C : F > P, la vitesse augmente, accélération positive.(phase 2)
Q11. À l’aide de la deuxième
loi de Newton et de la figure 3, estimer la valeur maximale de F, en
supposant que l’ascenseur vide pèse 2,0 tonnes et qu’il peut accueillir
21 personnes.
Masse d'une pesronne : 70 kg ; masse maximale totale : M= 21 x70 + 2 000 =3 470 kg.
Accélération maximale : 0,6 m s
-2.
F-P = Ma ; F = Ma+P = 3470 x0,6 +3470=5 552 ~ 5,6 10
3 N.