Mathématiques. Bac G Amérique du Sud 2025.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
... . .
.. ..
......


...
Exercice 1 4 points
Un étudiant mange tous les jours au restaurant universitaire. Ce restaurant propose des plats végétariens et des plats non végétariens.
- Lorsqu’un jour donné l’étudiant a choisi un plat végétarien, la probabilité qu’il choisisse un plat végétarien le lendemain est 0,9.
- Lorsqu’un jour donné l’étudiant a choisi un plat non végétarien, la probabilité qu’il choisisse un plat végétarien le lendemain est 0,7.
Pour tout entier naturel n, on note Vn, l’évènement « l’étudiant a choisi un plat végétarien le ne jour » et pn la probabilité de Vn.
Le jour de la rentrée, l’étudiant a choisi le plat végétarien. On a donc p1 = 1.
1. a. Indiquer la valeur de p2.
p2=0,9.
b. Montrer que p3 = 0,88. On pourra s’aider d’un arbre pondéré.

c. Sachant que le 3e jour l’étudiant a choisi un plat végétarien, quelle est la probabilité qu’il ait choisi un plat non végétarien le jour précédent ? On arrondira le résultat à 10−2..
0,07 / 0,88 ~0,08.
2. Recopier et compléter l’arbre pondéré ci-dessous :

3. Justifier que, pour tout entier naturel n >1, pn+1 = 0,2pn +0,7.
pn+1=0,9pn+0,7(1-pn)=0,2 pn+0,7.
4. On souhaite disposer de la liste des premiers termes de la suite (pn) pour n >1.
Pour cela, on utilise une fonction appelée repas programmée en langage Python dont on propose trois versions, indiquées ci-dessous.
a. Lequel de ces programmes permet d’afficher les n premiers termes de la suite (pn) ? Aucune justification n’est attendue.

Programme 1 :
Le second programme donne les n+1 termes et le troisième donne des valeurs supérieures à 1.
b. Avec le programme choisi à la question a. donner le résultat affiché pour n = 5.
p1=1 ; p2=0,9 ; p3=0,2 p2+0,7=0,2 *0,9+0,7=0,88.
p4=0,2 p3+0,7=0,2 *0,88+0,7=0,876.
p5=0,2 p4+0,7=0,2 *0,876+0,7=0,8752.
5. Démontrer par récurrence que, pour tout naturel n >1, pn = 0,125×0,2n−1+0,875.
Initialisation : p2 = 0,125 x0,2+0,875=0,9 est vérifié.
Hérédité : pn = 0,125×0,2n−1+0,875 est supposé vrai.
pn+1=0,2 pn +0,7 =0,2(0,125×0,2n−1+0,875)+0,7 = 0,125×0,2n+0,2x0,875+0,7=0,125×0,2n+0,875.
La prorpiété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang 2 et héréditaire ; elle est donc vraie pour tout entier naturel n.
6. En déduire la limite de la suite (pn).
0 < 0,2 < 1, donc 0,2n tend vers zéro si n tend vers plus l'infini.
pn+1 tend vers 0,875.

Exercice 2 . QCM. 5 points.
1. Deux équipes de footballeurs de 22 et 25 joueurs échangent une poignée de main à la fin d’un match. Chaque joueur d’une équipe serre une seule fois la main de chaque joueur de l’ autre équipe.
Affirmation 1 : 47 poignées de mains ont été échangées. Faux.
22 x25 =550.
2. Une course oppose 18 concurrents. On récompense indistinctement les trois premiers en offrant le même prix à chacun.
Affirmation 2. Il y a 4 896 possibilités de distribuer ces prix. Faux.
Nombre d'ensemble  à 3 éléments parmi 18 : (318)=18 x17 x16 / (2 x3)=816.

3. Une association organise une compétition de course de haies qui permettra d’établir un podium (le podium est constitué des trois meilleurs sportifs classés dans leur ordre d’arrivée). Sept sportifs participent au tournoi. Jacques est l’un d’entre eux.
Affirmation 3. Il y a 90 podiums différents dont Jacques fait partie. Vrai.
Jacques étant sur le podium, il a décroché l'une des trois premières places.
Si Jacques est premier, il y 6 possibilités pour le second et 5 possibilités pour le troisième ;  donc 30 podiums.
Si Jacques est second, il y 6 possibilités pour le premier et 5 possibilités pour le troisième ;  donc 30 podiums.
Si Jacques est troisième, il y 6 possibilités pour le premier et 5 possibilités pour le second ;  donc 30 podium.
Il y a 90 podium différents dont Jacques fait partie.
4. Soit X1 et X2 deux variables aléatoires de même loi donnée par le tableau ci-dessous :
xi
 -2
 -1
 2
 5
P(X=xi)
 0,1
 0,4
 0,3
 0,2
On suppose que X1 et X2 sont indépendantes et on considère Y la variable aléatoire somme de ces deux variables aléatoires.
Affirmation 4. P(Y = 4) = 0,25. Vrai.
Cet événement est réalisé dans 3 cas disjoints : X1 = -1 et X2 = 5 ; X1 = 2 et X2 = 2 ; X1 = 5 et X2 = -1 ;
P(Y=4) =P(X1 = -1) n P(X2 = 5) +P(X1 = 21) n P(X2 = 2) +P(X1 = 5) n P(X2 = -1).
P(Y=4) =0,4 x0,2 +0,3 x0,3 +0,2 x0,4 =0,25.

5. Un nageur s’entraîne dans l’objectif de parcourir le 50 mètres nage libre en moins de 25 secondes. Au fil des entraînements, il s’avère que la probabilité qu’il y parvienne s’établit à 0,85.
Il effectue, sur une journée, 20 parcours chronométrés sur 50 mètres. On note X la variable aléatoire qui compte le nombre de fois où il nage cette distance en moins de 25 secondes lors de cette journée.
On admet que X suit la loi binomiale de paramètres n = 20 et p = 0,85.
Affirmation 5
Sachant qu’il a atteint au moins 15 fois son objectif, une valeur approchée à 10−3 de la probabilité qu’il l’ait atteint au moins 18 fois est 0,434. Vrai.
P(X >15 (X >18)=P((X>15) n (X >18)) / P(X >15)=P(X >18) / P(X >15)=0,434.

... =  =
....
Exercice 3 6 points
On se propose d’étudier la concentration dans le sang d’un médicament ingéré par une personne pour la première fois. Soit t le temps (en heures) écoulé depuis l’ingestion de ce médicament.
On admet que la concentration de ce médicament dans le sang, en gramme par litre de sang, est modélisée par une fonction f de la variable t définie sur l’intervalle [0 ; +∞[.
Partie A : lectures graphiques.
On a représenté ci-dessus la courbe représentative de la fonction f .

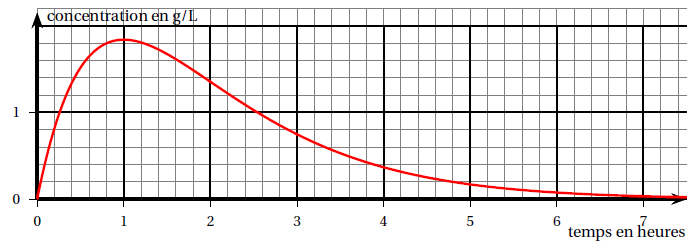
Avec la précision permise par le graphique, donner sans justification :
1. Le temps écoulé depuis l’instant de l’ingestion de ce médicament et l’instant où la concentration de médicament dans le sang est maximale selon ce modèle.
Environ 1 heure.
2. L’ensemble des solutions de l’inéquation f (t )>1.
 t appartient à [0,25  ; 1,95] heure.
3. La convexité de la fonction f sur l’ intervalle [0; 8].
Fonction convexe sur [0 ; 2,5 ) et concave sur [2,5 ; 8 ].

Partie B : détermination de la fonction f
On considère l’équation différentielle
(E) : y′+ y = 5e−t ,
d’inconnue y, où y est une fonction définie et dérivable sur l’intervalle [0 ; +∞[.
On admet que la fonction f est une solution de l’équation différentielle (E).
1. Résoudre l’équation différentielle (E′) : y′+ y =0.
y = A exp(-t) avec A une constante réelle.
2. Soit u la fonction définie sur l’intervalle [0 ; +∞[ par u(t )= ate−t avec a réel.
Déterminer la valeur du réel a telle que la fonction u soit solution de l’équation (E).
Calcul de la dérivée u'(t) en posant v =a t et w = exp(-t) ; v' = a ; w' = -exp(-t).
v' w+v w' = a exp(-t) -at exp(-t) =a(1-t) exp(-t).
Repport dans (E) : a(1-t) exp(-t)+at exp(-t) =5 exp(-t).
a exp(-t)  = 5 exp(-t).
a = 5.
3. En déduire l’ensemble des solutions de l’équation différentielle (E).
Solution générale de (E') + solution particulière de (E) :
f(t) = A exp(-t) + 5t exp(-t).
4. La personne n’ayant pas pris ce médicament auparavant, on admet que f (0) =0.
Déterminer l’expression de la fonction f .
f(0) = A =0 ; f(t) = 5t exp(-t).

Partie C : étude de la fonction f
Dans cette partie, on admet que f est définie sur l’intervalle [0 ; +∞[ par f (t ) = 5te−t .
1. Déterminer la limite de f en +∞.
En plus l'infini, exp(-t) tend vers zéro ; par produit des limites, f(t) tend vers zéro.
Interpréter ce résultat dans le contexte de l’exercice.
Au bout d'un temps suffisamment long, la concentration du médicament dans le sang est nulle.
2. Étudier les variations de f sur l’intervalle [0 ; +∞[ puis dresser son tableau de variation complet.
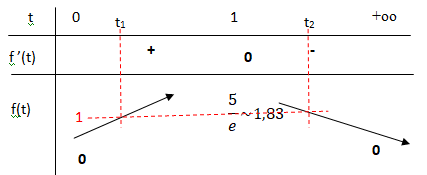
Calcul de la dérivée f '(t) en posant u =5 t et v = exp(-t) ; u' = 5 ; v' = -exp(-t).
u' v+u v' = 5 exp(-t) -5t exp(-t) =5(1-t) exp(-t).
f '(t) a le signe de (1-t).

3. Démontrer qu’il existe deux réels t1 et t2 tels que f (t1) = f (t2) =1.
On donnera une valeur approchée à 10−2 des réels t1 et t2.
Sur [0 ; 1], f(t) est continue et strictement croissante de 0 à 1,83.
f(t1)=1 appartient à l'intervalle. [0 ; 1,83].
D'après le corollaire du théorème des valeurs intermédiaires, l'équation f(t) = 1 admet une solution unique sur cet intervalle.
Sur [1 ; +oo[ f(t) est continue et strictement décroissante de 1,83 à 0.
f(t2)=1 appartient à l'intervalle. [1,83 ; 0].
D'après le corollaire du théorème des valeurs intermédiaires, l'équation f(t) = 1 admet une solution unique sur cet intervalle.
t1 ~0,26 ; t2 =2,54.
4. Pour une concentration du médicament supérieure ou égale à 1 gramme par litre de sang, il y a un risque de somnolence.
Quelle est la durée en heures et minutes du risque de somnolence lors de la prise de ce médicament ?
t2-t1=2,54-0,26=2,28 h =2 h 17 min.
Partie D : concentrationmoyenne
La concentration moyenne du médicament (en gramme par litre de sang) durant la première heure est donnée par l'intégrale suivante.
Calculer cette concentration moyenne.
On donnera la valeur exacte puis une valeur approchée à 0,01 près.
Intégration par parties en posant u = 5t et v ' = exp(-t) ; u' =5 ; v = -exp(-t).

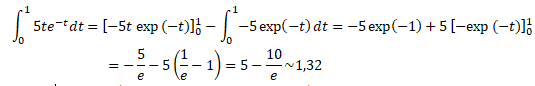Exercice4. 5 points
L’espace est muni d’un repère orthonormé..

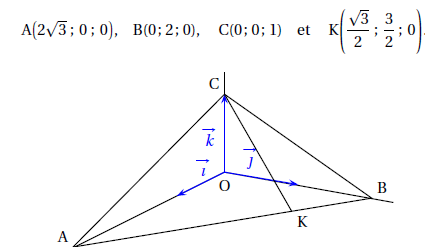1. Justifier qu’une représentation paramétrique de la droite (CK) est :
x = 3½t /2 ; y=1,5t ; z=1-t avec t réel.

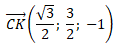
x = 3½ /2t +xC =3½ /2 t.
y = 3t / 2 +yC =3t / 2.
z = -t+zC =-t+1.
2. Soit M(t ) un point de la droite (CK) paramétrée par un réel t .
Établir que OM(t )=(4t2-2t+1)½.
OM(t)2 =( 3½ /2 t)2 +(3/2 t)2 +(-t+1)2 =3 / 4t2 +9/4t2+t2-2t+1=4t2-2t+1.
OM(t )=(4t2-2t+1)½.
3. Soit f la fonction définie et dérivable sur R par f (t )=OM(t ).
a. Étudier les variations de la fonction f sur R.
b. En déduire la valeur de t pour laquelle f atteint son minimum.
f '(t) =0,5(8t-2) /(4t2-2t+1)½= (4t-1) / (4t2-2t+1)½.
Si t > 0,25, f '(t) >0 et f(t) est strictement croissante.
Si t < 0,25, f '(t) < 0 et f(t) est strictement décroissante.
Si t = 0,25, f '(t) = 0 et f(t) présente un miniimum.
4. En déduire que le point H(3½ /8 ; 3 / 8 ; 3 /4) est le projeté orthogonal du point O sur la droite (CK).

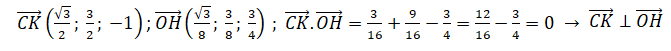5. Démontrer, à l’aide de l’outil produit scalaire, que le point H est l’orthocentre (intersection des hauteurs d’un triangle) du triangle ABC.
Dans l'hypothèse ou H est l'orthocentre du triangle ABC, les produits scalaires suivants doivent être nuls.

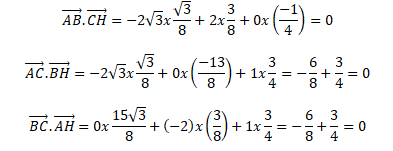
L'hypothèse étant vérifiée,  H est l'orthocentre du triangle ABC.
6. a. Démontrer que la droite (OH) est orthogonale au plan (ABC).

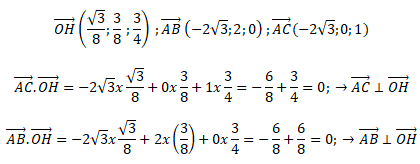
La droite (OH) étant orthogonale à deux vecteurs non colinéaires du plan ABC, cette droite est orthogonale au plan ABC.
b. En déduire une équation du plan (ABC).
3½/8x +3y / 8 +3z/4 +d =0.
3½/x +3y  +6z +d =0.
B(0 ; 2 ; 0) appartient à ce plan :
6+d =0 ; d = -6.
3½/x +3y  +6z -6 =0.
7. Calculer, en unité d’aire, l’aire du triangle ABC.

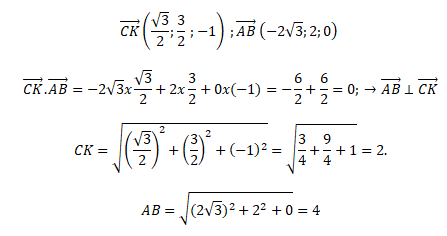
Aire du triangle ABC : CK x AB / 2 = 2 x4 /2 = 4 unités d'aire.





  
menu