Mathématiques, physique chimie. Bac STL 09 / 2025.

Exercice 1 (5,5 points) : radioactivité et cinétique chimique
Les parties A et B sont indépendantes et présentent chacune une situation concrète dont la modélisation relève d’une équation différentielle du premier ordre.
Partie A : DANS LE DOMAINE DE LA RADIOACTIVITÉ
La tomographie par émission de positons (TEP ou PETscan) repose sur l’injection intraveineuse d’une substance (le « traceur ») marquée par un atome radioactif, le fluor 18 ou le carbone 11, qui émet des particules particulières, les positons. Le traceur est choisi pour se fixer sur un organe ou un tissu.
D’après https://www.vidal.fr/sante/examens-tests-analyses-medicales/tomographie-emission-positons-petscan.html
1. Le fluor 18 (¹⁸₉F) est un isotope radioactif du fluor. Donner la composition du noyau de l’isotope 18 du fluor.
9 protons et 18-9 = 9 neutrons.
Le fluor 18 se désintègre spontanément pour donner l’isotope 18 de l’oxygène (¹⁸₈O). L’équation de cette réaction nucléaire s’écrit :
¹⁸₉F--> ¹⁸₈O +^Y_ZX
2. Déterminer Y et Z. Préciser le type de cette désintégration (a, ß^-ou ß⁺).
Conservation de la charge : 9=8+Z ; Z = 1.
Conservation du nombre de nucléons : 18 = 18+Y ; Y = 0.
^Y_ZX est ⁰₁e, positon, radioactivité de type ß⁺.
Lors de l’utilisation du traceur radioactif, et afin de déterminer les doses à injecter, on définit « l’activité du traceur », notée A, comme le nombre de désintégrations par seconde, pour un échantillon donné. Elle est exprimée en becquerel (Bq).
Pour mener l’examen, il faut injecter une dose de traceur dont l’activité est proportionnelle à la masse du patient. L’activité du traceur à injecter est calculée en multipliant la masse du patient par une constante A_m=3,6 MBq·kg⁻¹. La durée d’un tel examen est environ de deux heures.
3. Sachant qu’une mole de traceur possède une activité A=63,4 GBq, montrer que la quantité de matière n à injecter pour un patient de masse m=60 kg est environ égale à 3,4×10⁻³ mol.
3,6 x60 =216 MBq = 0,216 GBq.
0,216 / 63,4=3,4×10⁻³ mol.
Le nombre N₀ de noyaux de fluor 18 initial dans la dose injectée est de 1,8×10¹⁵. On modélise la désintégration de ces 1,8×10¹⁵ noyaux par une fonction f qui au temps t, exprimé en minutes, associe le nombre f't) de noyaux de fluor 18. On obtient la représentation de la fonction f donnée dans le document suivant..
On rappelle que le temps de demi-vie, t_½, correspond à la durée au bout de laquelle la moitié des noyaux radioactifs initialement présents se sont désintégrés.
4. [Mathématiques] Résoudre graphiquement l’équation f(t)= 0,9×10¹⁵ .

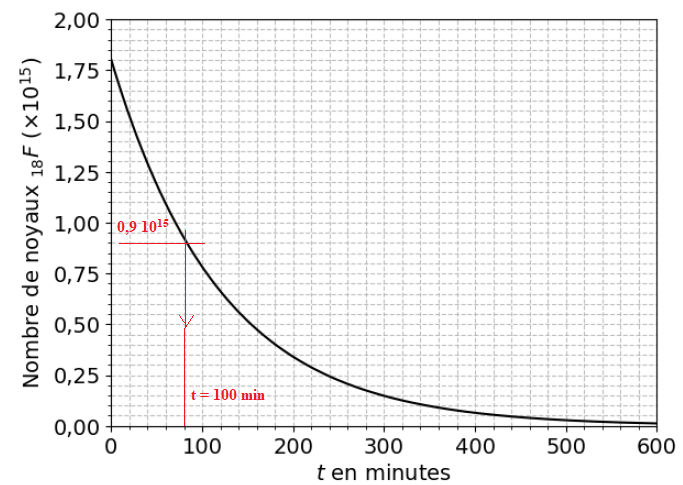
On admet que, pour tout réel 𝑡 positif, f(t)=1,8×10¹⁵×exp(-lt) , où l est un réel.
5. [Mathématiques] Résoudre algébriquement l’équation 0,9× 10¹⁵= 1,8× 10¹⁵× exp(-80x). On note l la solution de cette équation. Donner une valeur approchée de l à 10⁻⁴.
0,9 / 1,8 = exp(-80x) ; 0,5 = exp(-80 x) ;
ln(0,5) = -80 x ; ln(2) = 80 x ; x = ln(2) / 80 ~0,0087.
La relation entre la grandeur l et le temps de demi-vie t½ s’écrit : l=ln2/ t½.
6. Nommer la grandeur l.
Constant radioactive.
7. La valeur de la demi-vie du carbone 11 est d’environ 20 minutes. À partir des résultats obtenus à la question 4 et sachant que la durée d’un examen est d’environ deux heures, expliquer pourquoi on peut être amené à privilégier l’utilisation du fluor 18 pour certains examens.
Pour le fluor 18 la demi-vie est égale à ln(2) / 0,0087 ~80 min ou 1 h 20 min.
On privilégie le fluor 18 car sa demi vie est du même ordre de grandeur que la durée de l'examen.

Partie B : DANS LE DOMAINE DE LA CINÉTIQUE
La vitamine C, ou acide L-ascorbique, contribue au bon fonctionnement de l’organisme. Présente dans les fruits et légumes frais, cette vitamine est fragile et disparait rapidement après leur cueillette. En l'absence de dioxygène, la dégradation de la vitamine C suit une cinétique d'ordre 1.
On modélise la concentration en acide L-ascorbique dans un jus de fruit par une fonction dérivable g qui, au temps t, exprimé en heures, associe la concentration en acide L-ascorbique, exprimée en mmol·L⁻¹. On note g′ la fonction dérivée de la fonction g.
On admet que, pour tout réel positif t, g(t)=2,5× exp( −0,0026 t). Une représentation graphique de la fonction g est présentée.

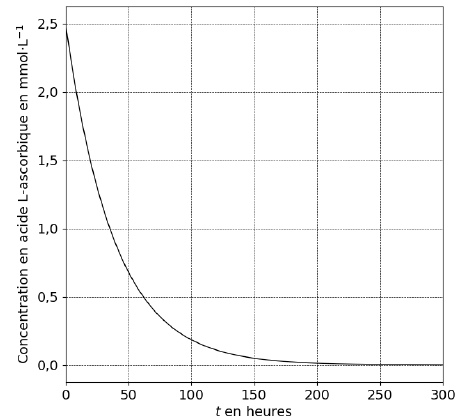
La vitesse de disparition v_disp de l’acide L-ascorbique est −dg / dt.
On admet que, pour tout réel t positif, la vitesse de disparition de l’acide L-ascorbique est donnée par
v_disp(t)=0,0065 exp(−0,0026 t).
8. [Mathématiques] Déterminer lla limite en +oo de v_disp(t).
Quand t tend vers +oo, exp(-0,0026t) tend vers zéro ; v_disp tend vers zéro.
9. Identifier le facteur cinétique expliquant que la vitesse de disparition de l’acide L-ascorbique tend vers 0.
La concentration en acide L-ascorbique diminue au cours du temps ; la concentration est un facteur cinétique.
On remarque que l’évolution de la concentration en acide L-ascorbique dans un jus de fruit au cours du temps à une température q inférieure à 25 °C suit l’allure de la courbe représentée sur le graphique ci-dessous.

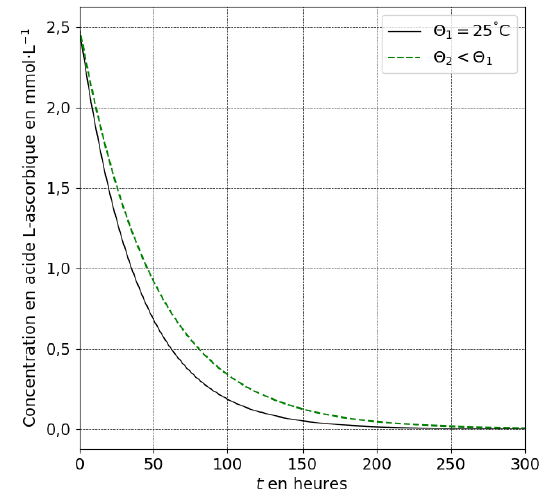
10. Déduire, de l’analyse de la figure, une technique courante pour conserver la teneur en vitamine C dans un jus de fruit.
Conserver le jus de fruit au réfrigérateur.
EXERCICE 2 (6,5 points)
(physique-chimie)
Les additifs alimentaires E280 et E281
Les additifs alimentaires E280 et E281 sont utilisés pour limiter l’apparition des moisissures, par exemple dans certains fromages ou pains industriels. L’additif E280 est l’acide propanoïque de formule C₂H₅−COOH, il est liquide à température ambiante. L’additif E281 est le propanoate de sodium de formule C₂H₅−COONa, qui lui se présente sous forme d’une poudre blanche à température ambiante.
Données : On admettra que toutes les mesures sont effectuées à 25 °C.
- Couple C₂H₅−COOH / C₂⁄H₅−COO⁻ à 25 °C : Ka=1,35×10⁻⁵ et pKa=4,87
- Masse molaire du propanoate de sodium : M=96,0 g·mol⁻¹
Une solution S d’acide propanoïque, de concentration en quantité de matière de soluté C=1,00×10⁻² mol·L⁻¹, a un pH mesuré de 3,44. L’acide propanoïque est un acide faible.
1. Écrire l’équation de la réaction de l’acide propanoïque avec l’eau.
C₂H₅−COOH aq + H₂O(l) =C₂⁄H₅−COO⁻aq +H₃O⁺aq.
2. Expliquer ce que signifie la phrase : « L’acide propanoïque est un acide faible. »
La réaction de cette acide avec l'eau est partielle.
3. Déterminer, entre C₂H₅−COOH(aq) et C₂H₅−COO⁻(aq), l’espèce chimique prédominante dans la solution S. On pourra utiliser un diagramme de prédominance pour justifier la réponse.

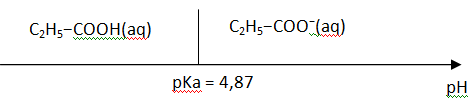
A pH < pKa, la forme acide C₂H₅−COOH(aq) prédomine.
4. Montrer que, dans la solution S, la concentration en quantité de matière en ion oxonium [H₃O⁺(aq)] a pour valeur 3,63×10⁻⁴ mol·L⁻¹.
[H₃O⁺(aq)] = 10^-pH = 10^-3,44 =3,63×10⁻⁴ mol·L⁻¹
5. À l’aide de l’équation de la réaction de l’acide propanoïque avec l’eau, écrire la relation entre la concentration en ions oxonium [H₃O⁺(aq)] et la concentration en ions propanoate [C₂H₅COO⁻ (aq)] dans la solution S.
La solution est électriquement neutre et à pH=3,44, HO^- est négligeable.
[C₂⁄H₅−COO⁻aq]= [H₃O⁺aq].
Le coefficient de dissociation a de l’acide propanoïque dans l’eau s’écrit : a= [C₂H₅COO⁻ (aq)] / C
6. Montrer, en expliquant la démarche, que la valeur de ce coefficient est 0,0363.
Ka = [C₂⁄H₅−COO⁻aq] [ [H₃O⁺aq] / [C₂H₅−COOH aq].
C = [C₂H₅−COOH aq]+ [C₂⁄H₅−COO⁻aq].
[C₂⁄H₅−COO⁻aq] << [C₂H₅−COOH aq].
C = [C₂H₅−COOH aq]
Ka ~[C₂⁄H₅−COO⁻aq] [H₃O⁺aq] / C.= a [H₃O⁺aq].
a =Ka / [H₃O⁺aq] =1,35 10^-5 / (3,63×10⁻⁴ )=0,0372.
7. Expliquer en quoi le résultat précédent confirme que l’acide propanoïque est un acide faible.
a <<1, l’acide propanoïque est un acide faible.
On dilue 10 fois la solution S. On obtient la solution S₁ dont le pH est égal à 3,94.
8. Expliquer comment évolue la valeur du coefficient de dissociation a lorsque l’on dilue la solution S. Justifier la réponse avec ou sans calcul.
C₂H₅−COOH aq + H₂O(l) =C₂⁄H₅−COO⁻aq +H₃O⁺aq.
En diluant 10 fois la solution, on déplace l'équilibre dans le sens direct.
a =Ka / [H₃O⁺aq] =1,35 10^-5 / 10^−3,94 =0,118.
On prélève 200 mL de la solution S. On pèse une masse égale à 0,192 g de propanoate de sodium C₂H₅−COO⁻,Na⁺ que l’on introduit dans la solution S et on agite. On néglige l’augmentation de volume lors de l’ajout du propanoate de sodium. Le mélange ainsi réalisé sera nommé S₂. Le pH du mélange S₂ est égal à 4,87. On réalise trois expériences en réalisant différents ajouts de solutions dans le mélange S₂. Les résultats sont présentés.

Expérience 1 : ajout de 10 mL de solution d’acide chlorhydrique de concentration 1,0×10⁻² mol·L⁻¹ dans un volume v de S₂	pH mesuré : 4,82
Expérience 2 : ajout de 50 mL d’eau distillée dans un volume v de S₂	pH mesuré = 4,88
Expérience 3 : ajout de 10 mL de solution d’hydroxyde de sodium (base) de concentration 1,0×10⁻² mol·L⁻¹ dans un volume v de S2	pH mesuré = 4,91

9. Justifier que la solution est une solution tampon, en utilisant les résultats des trois expériences.
Lors de l'ajout modéré d'une base forte ou d'un acide fort, le pH de la solution varie très peu. La solution S est une solution tampon.
10. En utilisant la relation suivante, pH=pKa+log[C₂H₅−COO ⁻ (aq) ] / [C₂H₅−COOH](aq)] et les informations précédentes, déterminer une relation entre la valeur de la concentration de l’acide propanoïque et celle de la concentration de sa base conjuguée dans la solution S₂.
log[C₂H₅−COO ⁻ (aq) ] / [C₂H₅−COOH](aq)]= pH-pKa = 4,87 -4,87 =0 = log(1).
.[C₂H₅−COO ⁻ (aq) ] = [C₂H₅−COOH](aq)].