EXERCICE 3 (4 points)
(Mathématiques)
Dans cet exercice, les quatre questions sont indépendantes.
Question 1 Pour cette question, indiquer, en justifiant, la lettre correspondant à la réponse
exacte.
On considère la fonction f définie sur R par f(x) = (2+5x) exp(3x).
On admet que f est dérivable sur R et on note f ′ sa dérivée.
Pour tout x appartenant à R, on a :
Calcul de f '(x) en posant u = 2+5x et v = exp(3x).
u' = 5 ; v' = 3 exp(x).
u'v+v'u = 5 exp(3x) + 3(2+5x) exp(3x) = (11+15x) exp(3x).
Réponse C.
.
Question 2On considère l’équation différentielle (E) : y' = −3y + 5,
où y est une fonction de la variable x, définie et dérivable sur R.
Déterminer les fonctions définies sur R, solutions de l’équation différentielle (E).
Solution générale de y'+3y=0 : f(x) = A exp(-3x) avec A une constante réelle.
Solution particulière de E : g(x) = 5 /3.
Solution générale de E : f(x) +g(x) = A exp(-3x) +5 /3.
Question 3
Déterminer la forme exponentielle du nombre complexe z = −6*3
½ + 6i.
Module de z : ((-6 *3
½)
2 +6
2)
½=144
½ = 12.
z / |z| = -3
½/2 +0,5 i = cos (5
p/6) + i sin (5
p/6).
z = 12 exp(5 i
p / 6).
Question 4
Les fonctions f et g définies sur R respectivement
par f(x) =0,5 x
2+1 et g(x) =x + 5 sont
représentées sur le graphique suivant par la
courbe C, courbe représentative de la fonction f et
la droite
D, courbe représentative de la fonction g.
Lire graphiquement les positions relatives des
courbes représentatives C de la fonction f et
D de
la fonction g puis montrer que l’aire de la partie
colorée comprise entre la courbe C et la droite
D
vaut 18 unités d’aire.
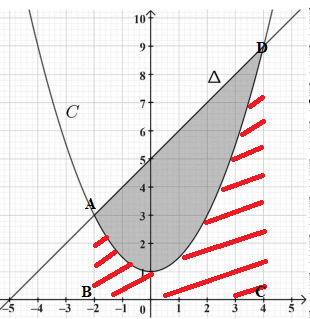
Pou x < -2 et x >4, la courbe C est au dessus de
D.
Pour x appartenant à ]-2 ; 4[, la courbe
D est au dessus de C.
Primitive de f(x) : F(x) = 0,5 / 3 x
3+x.
Aire hachurée en rouge : F(4)-F(-2) =0,5 / 3 *4
3 +4 -(0,5 / 3 *(-2)
3-2)=32 /3 +4 +4 /3+2=18.
Aire du trapèze ABCD : (3+9) * 6 /2 =36.
Aire hachurée en gris : 36-18 = 18 unités d'aire.
EXERCICE 4 : (5 points)
(physique-chimie)
L’importance des coulées en natation.
Lors des Jeux Olympiques de Paris en 2024, le nageur français Léon Marchand a
remporté 4 médailles d’or. Ce sont les coulées réalisées lors de ses courses qui ont
marqué les esprits.
On appelle coulée la phase pendant laquelle le nageur se déplace sous l’eau après un
plongeon ou un virage.
Partie 1 – Étude mécanique des coulées.
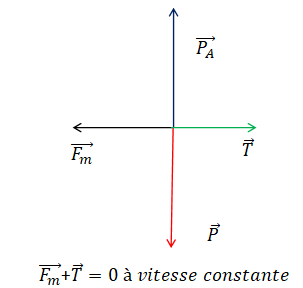
Lorsqu’un nageur de masse m se déplace dans un fluide, il est soumis à plusieurs forces :
- son poids P ;
- la poussée d’Archimède P
A (direction : verticale, sens : du bas vers le haut) ;
- la résultante des forces de frottements ou trainée hydrodynamique T ;
- la résultante des forces motrices F
m exercées par l’eau sur le nageur.
La direction de la résultante des forces de frottements hydrodynamique T et celle de la
résultante des forces motrices F
m sont horizontales.
Q1. Représenter sur un schéma, sans notion d’échelle, les forces auxquelles est soumis
un nageur lors d’une coulée.
On suppose que le nageur effectue une coulée à profondeur constante.
Q2. En appliquant le principe fondamental de la dynamique, établir la relation
mathématique liant les forces T et F
m lorsque le nageur réalise une coulée à profondeur
et à vitesse constantes.
Lors de son titre au 200 m papillon aux championnats du monde à Fukuoka en 2023,
Léon Marchand a effectué une dernière coulée de 13,88 m en 7,46 s.
Q3. Calculer la vitesse moyenne v
1 à laquelle il a effectué cette coulée.
v
1=13,88 / 7,46=1,86 m /s.
On suppose que la coulée a été effectuée à profondeur constante et à une vitesse
constante et égale à v
1. D’autres analyses ont montré que la valeur de la trainée
hydrodynamique peut s’écrire sous la forme T = kv
12, avec k = 22 kg∙m
-1
.
Q4. Montrer que la valeur F
m de la résultante des forces motrices exercées par l’eau sur
le nageur, lors de cette dernière coulée, est voisine de 76 N.
F
m = T = 22 x1,86
2 ~ 76 N.
Q5. Calculer le travail W
m de la force F
m lors de cette coulée, puis sa puissance P
m.
W
m =13,88 F
m =13,88 x 76=1057 ~1,1 10
3 J.
P
m =W
m / durée =1057 / 7,46 = 1,4 10
2 W.
La vitesse moyenne de nage de Léon Marchand lors du dernier 50 m de course est
d’environ v
2 = 1,64 m∙s
-1. Pour parcourir les 13,88 m en nageant à la surface à cette
vitesse, il aurait dû développer une puissance de l’ordre de 225 W.
Q6. Conclure sur l’intérêt des coulées pour les nageurs de compétition.
La glisse en coulée est plus efficace qu'en surface.
Partie 2 – Coulées et acide lactique
Le glucose est une source d’énergie facilement métabolisable par l’organisme humain,
au profit des cellules musculaires. Lors d’un effort sportif, le glucose est dégradé par
l’organisme en acide pyruvique. En l’absence de dioxygène, l’acide pyruvique est à
son tour dégradé en acide lactique. Ces diverses transformations chimiques
permettent à l’organisme de produire l’énergie nécessaire au bon fonctionnement des
muscles.
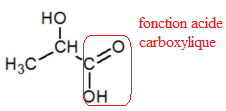
Q7. Justifier que l’acide lactique appartient à la famille des acides carboxyliques.
Dans la suite de l’exercice la molécule d’acide lactique est notée AH. Les ions lactates,
base conjuguée de l’acide lactique sont notés A
-
.
Q8. L’acide lactique réagit avec l’eau présente dans le corps humain pour former des
ions lactate. Écrire l’équation-bilan de cette réaction acido-basique.
AH aq + H
2O(l) = A
-aq + H
3O
+aq.
Lors d'un effort intense, l'augmentation de la quantité d’ions H
3O
+
(aq) dans les cellules
musculaires rend le sang plus acide ce qui peut provoquer une diminution de la
capacité à poursuivre l'effort.
Q9. Indiquer en justifiant comment la production d’ions lactates par l’organisme peut
réguler le pH musculaire en consommant une partie des ions H
3O
+
(aq) produits en
excès lors d’un effort musculaire.
Le lactate agit comme un tampon permettant de réguler le pH musculaire.
A
-aq + H
3O
+aq -->AH aq + H
2O(l).