Mathématiques. Bac G Nouvelle Calédonie 2025.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.
.		 . .


.. ..
......


...
Exercice 1 5 points
   On dispose d’un sac et de deux urnes A et B.
- Le sac contient 4 boules : 1 boule avec la lettre A et 3 boules avec la lettre B.
- L’urne A contient 5 billets : 3 billets de 50 euros et 2 billets de 10 euros.
- L’urne B contient 4 billets : 1 billet de 50 euros et 3 billets de 10 euros.
Un joueur prend au hasard une boule dans le sac :
- si c’est une boule avec la lettre A, il prend au hasard un billet dans l’urne A.
- si c’est une boule avec la lettre B, il prend au hasard un billet dans l’urne B.
 On note les évènements suivants :
 • A : le joueur obtient une boule avec la lettre A.
• C : le joueur obtient un billet de 50 euros.
1. Recopier et compléter l’arbre ci-dessous représentant la situation.

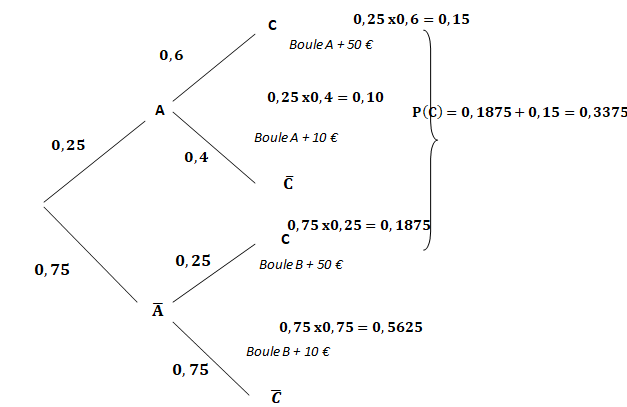2. Quelle est la probabilité de l’évènement « le joueur obtient une boule avec la lettre A et un billet de 50 €?
0,25 x0,6= 0,15.
 3. Démontrer que la probabilité P(C) est égale à 0,337 5.
Formule des probabilités totale : P(A n C) + P (non A n C) =0,15 + 0,1875=0,3375.
 4. Le joueur a obtenu un billet de 10 euros. L’affirmation « Il y a plus de 80% de chances qu’il ait au préalable obtenu une boule avec la lettre B » est-elle vraie ? Justifier.
Pnon C ( non A) =P(non A n non C) / P(non C) =P(non A n non C) / (1- P(C))=0,75 x 0,75 / (1-0,3375)~0,85.
L'affirmation est vraie.
 5. On note X1 la variable aléatoire qui donne la somme, en euros, obtenue par le joueur. Exemple : si le joueur obtient un billet de 50 €, on a X1 = 50. Montrer que l’espérance E(X1) est égale à 23,50 et que la variance V (X1) est égale à 357,75.
Loi de probabilité de X1 :
ki
 10
 50
P(Xi = ki)
 0,6625
 0,3375
E(X1) = 10 x0,6625 +50 x0,3375 =23,5.
V(X1)=E(X12) -[E(X1)]2 =(100 x0,6625 +50 x50 x0,3375)-23,52=357,75.
 6. Après avoir remis la boule dans le sac et le billet dans l’urne où il a été pris, le joueur joue une deuxième partie. On note X2 la variable aléatoire qui donne la somme obtenue par le joueur lors de cette deuxième partie. On note Y la variable aléatoire ainsi définie : Y = X1 + X2.
a. Montrer que E(Y ) = 47.
E(Y) = 2 E(X1) = 2 x23,5 = 47.
b. Expliquer pourquoi on a V (Y ) = V (X1)+V (X2)
Le billet et la boule ont été remis ; les deux tirages sont donc indépendants. Les variables aléatoires X1 et X2 sont donc indépendantes.
V(Y) = V(X1) + V(X2) = 2 x357,75=715,5.
7. Le joueur joue de même une troisième, une quatrième,..., une centième partie. On définit donc de la même façon les variables aléatoires X3, X4, ...,X100. On note Z la variable aléatoire définie par Z = X1 + X2 +...+ X100. Démontrer que la probabilité que Z appartienne à l’intervalle ]1950 ; 2750[ est supérieure ou égale à 0,75.
E(Z) = E(X1) + E(X2) +...+E(X100)=100 x23,5 =2 350.
V(Z) = V(X1) + V(X2) +...+V(X100)=100 x357,75 =35 775.
L'inégalité de Bienaymé-Tchebychev s'écrit : P(|Z-E(Z)| < t) > 1-V(Z) / t2.
P( |Z-2350| < t ) > 1-35 775 / t2.
 |Z-2350| < t est équivalent à : 2350-t < Z < 2350+t.
On cherche P(Z) appartient à ]1950 ; 2350[. On prend t = 400:
P(Z appartient à ]1950 ; 2750[ ) > 1- 35 775 / 4002.
1- 35 775 / 4002.~0,776 > 0,75.
 Donc la probabilité que Z appartienne à l’intervalle ]1 950 ; 2 750[ est supérieure ou égale à 0,75.

Exercice 2 . Géométrie. 4 points.
Dans l’espace rapporté à un repère orthonormé , on considère les points :
A(4 ; −4 ; 4), B(5 ; −3 ; 2), C(6 ; −2; ; 3), D(5; 1; 1)
1. Démontrer que le triangle ABC est rectangle en B.
AB2 =(5-4)2+(-3-(-4))2+(2-4)2=1+1+4=6.
CB2 =(5-6)2+(-3-(-2))2+(2-3)2=1+1+1=3.
AC2 =(6-4)2+(-2-(-4))2+(3-4)2=4+4+1=9.
AC2 =AB2 +CB2 .
D'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en B.

 2. Justifier qu’une équation cartésienne du plan (ABC) est : x − y −8 = 0.

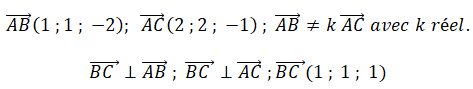
Les points A, B et C n'étant pas alignés, ils définissent un plan. Leurs coordonnées vérifient toute équation cartésienne du plan (ABC).
xA-yA-8 = 4+4-8 =0 est vérifiée.
xB-yB-8 = 5+3-8 =0 est vérifiée.
xC-yC-8 = 6+2-8 =0 est vérifiée.

On note d la droite passant par le point D et orthogonale au plan (ABC).
 a. Déterminer une représentation paramétrique de la droite d.
Coordonnées d'un vecteur directeur de la droite d : 1 ; -1 ; 0.
Représentation paramétrique de cette droite d :
 x = t+xD = t +5 avec t réel.
y = -t +yD = -t+1.
z = zD =1.

b. On note H le projeté orthogonal du point D sur le plan (ABC). Déterminer les coordonnées du point H.
Les coordonnées du point H vérifient à la fois l'équation cartésienne du plan (ABC) et la représentation paramétrique de la droite d.
xH-yH-8=0.
t+5 -(-t+1)-8=0 ; 2t-4=0 ; t = 2.
xH= 2+5 =7 ; yH = -2+1=-1 ; zH = 1.
H( 7 ; -1 ; 1).
 c. Montrer que DH = 2 *2½.
DH2 =(7-5)2+ ( -1-1)2+(1-1)2=4+4=8= 2*22.
DH = 2 *2½.

4. a. Montrer que le volume de la pyramide ABCD est égal à 2. On rappelle que le volume V d’une pyramide se calcule à l’aide de la formule : V = 1 /3 ×B ×h où B est l’aire d’une base de la pyramide et h la hauteur correspondante.
Base  : triangle ABC rectangle en B.
Aire de la base : AB * BC / 2 = 6½ x 3½ / 2 = 18½ /2 =2½ x 3 /2.
Hauteur DH = 2 x 2½.
Volume de cette pyramide : V = 2½ x 3 /2 x 2 x 2½ / 3 =2.

b. On admet que l’aire du triangle BCD est égale à 42½ / 2 . En déduire la valeur exacte de la distance du point A au plan (BCD).
La distance du point A au plan (ABC), notée x, est la hauteur issue de A de la pyramide ABCD
Volume de la pyramide ABCD = aire du triangle BCD * x / 3=2.
x = 2 *3 *2 / 42½ =2 * 6 / (6½ *7½)=2 * 6½ *7½ / 7= 2*42½ / 7.

... =  =
....
Exercice 3. 6 points
On considère n un entier naturel non nul. On considère la fonction fn définie sur l’intervalle [0 ; 1] par : fn(x) = x n e 1−x . On admet que la fonction fn est dérivable sur [0 ; 1] et on note f ′ n sa fonction dérivée.
Partie A.
 Dans cette partie on étudie le cas où n = 1. On étudie donc la fonction f1 définie sur [0 ; 1] par : f1(x) = xe 1−x .
1. Montrer que f ′ 1 (x) est strictement positive pour tout réel x de [0 ; 1[.
 On pose u = x et v = exp(1-x) ; u' = 1 ; v' = -exp(1-x).
f ′ 1 (x)  =u'v+v'u = (1-x)exp(1-x).
exp(1-x) >0 ; 1-x >0 sur [0 ; 1[.
f ′ 1 (x) est strictement positive pour tout réel x de [0 ; 1[.
 
 2. En déduire le tableau de variations de la fonction f1 sur l’intervalle [0 ; 1].

 3. En déduire que l’équation f1(x) = 0,1 admet une unique solution dans l’intervalle [0 ; 1].
La fonction f1 est continue (car dérivable) et strictement croissante sur [0 ; 1], avec f1(0) = 0 < 0,1 et f1(1) = 1 > 0,1 : d’après le corollaire du théorème des valeurs intermédiaires, l’équation f1(x) = 0,1 admet une solution unique dans [0 ; 1].

 Partie B
On considère la suite (un) définie pour tout entier naturel n non nul par

 On admet que u1 = e−2.
1. a. Justifier que pour tout x appartenant à [0 ; 1] et pour tout entier naturel n non nul, 0 < x n+1 < x n.
x >0 ; donc xn >0 ;
0 < x < 1 : 0*  xn < x * xn < 1* xn ; 0 < x n+1 < x n.

b. En déduire que pour tout entier naturel n non nul, 0 < un+1 < un.
e1-x >0 ; 0 < x n+1e1-x < x n e1-x ;
d'après la positivité de l'intégration :

c. Montrer que la suite (un) est convergente.
un+1 < un, la suite (un) est décroissante.
0 < un : la suite est minorée par zéro.
D'après le théorème de la convergence monotone, la suite (un) est convergente.

2. a. À l’aide d’une intégration par parties, démontrer que pour tout entier naturel n non nul on a : un+1 = (n +1)un −1.
On pose u'(x) = e1-x et v(x) = xn+1.
u(x) = -e1-x ; v'(x)=(n+1) xn.

un+1 = (n +1)un −1.

 b. On considère le script Python ci-dessous définissant la fonction suite() :
Recopier et compléter le script Python ci-dessous pour que la fonction suite() renvoie la valeur de
from math import exp
def suite()
 u=exp(1)-2
for n in range (1, 8):
u=(n+1)*u-1
return u

3. a. Démontrer que pour tout entier naturel n non nul on a : un < e / ( n +1).
Dans l'intervalle d'intégration [0 ; 1 ] :
0 < x < 1 ; donc  1-x < 1 ; donc par croissance de la fonction exponentielle e1-x < e.
xn e1-x < xn e.
Par croissance de l'intégration :

b. En déduire la limite de la suite (un).
0 < un ; donc 0 < un < e / (n+1).
e / (n+1) tend vers zéro si n tend vers +oo.
D'après le théorème des gendarmes la limite de un est égale à zéro si n tend vers +oo.

Exercice 4. 5 points
1. On considère la fonction f définie sur l’intervalle ]0 ; +∞[ par : f (x) = ln(x)− x 2 .
Affirmation 1 : la limite en +oo de f(x) est -oo. Vrai.
f(x) = x2(ln(x) / x2 -1).
En -oo : par croissance comparée, la limite  de ln(x) / x2 est nulle.
La limite de (ln(x) / x2 -1). est égale à -1.
La limite de x2 est +oo.
Par produit des limites, la limite de f(x) est -oo.

 2. On considère l’équation différentielle (E) : −2y ′ +3y = sinx +8cos x.
On considère la fonction f définie sur R par : f (x) = 2cos x −sinx.
 Affirmation 2 : La fonction f est solution de l’équation différentielle (E).  Vrai.
f '(x) = -2sin(x) -cos (x).
Repport dans (E) : 4 sin(x)+2cos(x)+6 cos(x) -3sin(x) =sin(x)+8 cos(x) est vérifié.

3. On considère la fonction g définie sur l’intervalle ]0 ; +∞[ par : g(x) = ln(3x +1).
 On considère la suite (un) définie par u0 = 25 et pour tout entier naturel n : un+1 = g(un). On admet que la suite (un) est strictement positive. Affirmation 3 : La suite (un) est décroissante. Vrai.
u0=25 ; u1 =ln(76)~4,3 < 25.
Démonstration par récurrence :
initialisation :  u1 < u0 est vraie.
Hérédité : un+1 < un est supposé vrai.
3 un+1 < 3 un ; 3 un+1 +1< 3 un +1 ;
par croissance de la fonction ln : ln(3 un+1 +1) < ln(3 un +1 ).
un+2 < un+1. La relation est vraie au rang n+1.
Conclusion : la relation est vraie au rang zéro et héréditaire ; la relation est donc vraie pour tout entier n.

4. On considère une fonction affine h définie sur R. On note k la fonction définie sur R par k(x) = x 4 + x 2 +h(x).
Affirmation 4 : La fonction k est convexe sur R. Vrai.
h(x) = ax +b ; k'(x) = 4x3+2x+a.
k"(x) =12 x2+2 > 0.
La dérivée seconde étant positive sur R, la fonction k est convexe sur R.
 
5. Une anagramme d’un mot est le résultat d’une permutation des lettres de ce mot. Exemple : le mot BAC est possède 6 anagrammes : BAC, BCA, ABC, ACB, CAB, CBA.
Affirmation 5 : Le mot EULER possède 120 anagrammes. Faux.
Avec 5 lettres différentes le nombre d'anagrammes est égal à 5! =120.
EULER possédant deux lettres identiques, le nombre d'anagrammes est égal à 5! / 2! =60.





  
menu