Compétition de saut d'obstacles en Hobby Horse. Bac G Asie 09 /2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . .. . . . . .. .. ...... ... Cet exercice comporte trois parties indépendantes. L’objectif de la première partie est de déterminer par effet Doppler la vitesse du véhicule annonçant la compétition grâce à l’effet Doppler. L’objectif de la deuxième partie est de déterminer la qualité du crin synthétique du hobby horse par le phénomène de diffraction. L’objectif de la dernière partie est de déterminer les paramètres permettant d’améliorer le saut d’obstacle par une étude dynamique et cinématique. 1. Annonce de la compétition de hobby horse diffusée par le mégaphone d’une voiture. Pour diffuser l’information de la tenue de la compétition de saut d’obstacles en hobby horse, une voiture munie d’un mégaphone sillonne les rues de la ville dans laquelle l’évènement se déroule. En début d’annonce, une note est jouée pour capter l’attention des auditeurs. La voiture s’approche d’un citadin qui se trouve immobile sur le bord de la route. Ce dernier perçoit la fréquence sonore fR de la note diffusée par le mégaphone vérifiant la relation : fR =vson /(vson - v )∙fE. - fE est la fréquence de l’onde sonore émise par le mégaphone ; - v est la valeur de la vitesse du véhicule qui se rapproche du citadin (par rapport à celui-ci) ; - vson est la célérité du son dans l’air, considérée égale à 340 m∙s–1. Q1. Décrire l’effet Doppler. L'effet Doppler est le décalage de fréquence d'une onde observée entre les mesures à l'émission et à la réception, lorsque la distance entre émetteur et récepteur varie au cours du temps. Q2. À partir de la relation donnée pour la fréquence sonore perçue fR, justifier que le son entendu par le citadin est plus aigu que celui qu’il percevrait si le véhicule était à l’arrêt. Véhicule à l'arrêt : v=0 ; fR =∙fE. La voiture s'approche du citadin : vson - v  < vson ; vson /(vson - v ) > 1 ; fR >∙fE. Le son entendu par le citadin est plus aigu. Q3. En déduire la valeur de la vitesse v du véhicule sachant que le citadin perçoit un son de fréquence fR = 448 Hz et que le mégaphone du véhicule en approche émet un son de fréquence fE = 440 Hz. Indiquer si la voiture respecte ou non la vitesse maximale autorisée dans une zone limitée à 30 km∙h–1. vson - v =vson fE / fR ; v = vson (1-fE / fR )=340 (1-440 / 448)= 6,07 m /s ou 6,07 x3,6=21,9 km / h < vitesse maximale autorisée. 2. Préparation avant la compétition de hobby horse. Certains hobby horses ont une crinière composée de crins synthétiques. Afin de comparer le diamètre des crins synthétiques utilisés à celui des crins de cheval, on réalise l’expérience de diffraction schématisée. On utilise une diode laser de longueur d’onde l et un crin synthétique de diamètre a. Un écran est placé à une distance D du crin. La largeur L de la tache centrale de la figure de diffraction ainsi obtenue est mesurée directement sur l'écran. q est l’angle caractéristique de diffraction, de valeur très inférieure à un radian. Il a pour expression : q = l/a . Données : - distance crin-écran D = 2,00 m et son incertitude-type u(D) = 0,01 m ; - diode laser utilisée de longueur d’onde l = 650 nm et son incertitude-type u(l) = 10 nm ; - largeur de la tache centrale mesurée L = 1,80 cm et son incertitude-type u(L) = 0,05 cm ; - on se place dans l’approximation des petits angles telle que tan q ≈ q. - pour discuter de l’accord du résultat d’une mesure avec une valeur de référence, on utilise le quotient | x-xréf| / u(x)  avec x, la valeur mesurée, xréf la valeur de référence et u(x), l’incertitude-type associée à la valeur mesurée x. Q4. À l’aide de la figure , établir l’expression du diamètre a du crin synthétique en fonction de l, D et L. tan q ~ q = ½L / D. q = l/a ½L / D = l/a a = 2 l D / L . Q5. À l’aide des données, montrer que la valeur du diamètre a du crin synthétique utilisé pour fabriquer la crinière du hobby horse est voisine de 144 μm. a=2 x650 10-9 x 2,00 / 0,018=1,44 10-4 m =144 µm Q6. À l’aide des données, calculer la valeur de l’incertitude-type u(a) du diamètre du crin synthétique utilisé, donnée par la relation :u(a) = 144x[(u(l)/ l)2 +(u(L)/L)2+(u(D)/D)2]½. Préciser si le diamètre du crin synthétique choisi convient pour simuler le crin réel d’un cheval dont le diamètre de référence est égal à 140 μm. u(a) =ax[(10/ 650)2 +(0,05/1,8)2+(0,01/2)2]½=144 x3,2 10-2 =4,6 µ ~5 µm. a = 144 ±5 µm. Le diamètre du crin synthétique choisi convient pour simuler le crin réel d’un cheval. ... =  = .... 3. Étude cinématique du saut d’obstacles en hobby horse. Le saut d’obstacles en hobby horse est une discipline qui se rapproche du saut de haies en athlétisme, mais avec une difficulté supplémentaire puisqu’il faut tenir d’une main le bâton et de l’autre les rênes, ce qui ne permet donc pas d’équilibrer le corps en utilisant les bras comme balancier. On appellera hobbyhorseur le système {hobby horse + cavalier}. Ce système de masse m est modélisé par un point matériel assimilé à son centre de masse M. L’étude se fait dans le référentiel terrestre considéré comme galiléen. À l’instant t = 0, le hobbyhorseur ne touche plus le sol, il est à la verticale du point O, engagé dans son saut par-dessus l’obstacle constitué par la barre horizontale, placée à une hauteur H. Le centre de masse M(t=0) du hobbyhorseur a alors pour coordonnées x0 = 0 et y0 = h et sa vitesse initiale est représentée par le vecteur vitesse v0 incliné d’un angle a par rapport à l’horizontale. L’obstacle est à une distance x = D du point O. On suppose que la trajectoire du système s'effectue dans le plan xOy. 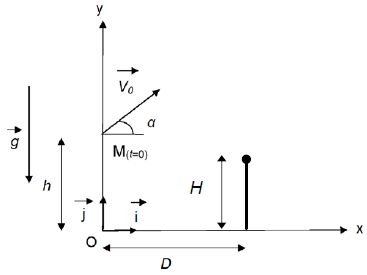Durant le saut, l’action exercée par l’air sur le système est considérée comme négligeable. On modélise la situation du saut d’obstacle sur la figure. Q7. En appliquant la deuxième loi de Newton dans le référentiel terrestre, déterminer les coordonnées ax(t) et ay(t) du vecteur accélération du centre de masse M du hobbyhorseur. Le système n'étant soumis qu'à son poids, verticale, vers le bas, valeur mg,, la seconde loi de Newton conduit à : ax =0 ; ay = -g. Q8. Établir les équations horaires x(t) et y(t) décrivant le mouvement du centre de masse M du hobbyhorseur lors du saut. La vitesse est une primitive de l'accélération : vx = constante ; vy = -gt + constante. A l'instant initial : vx = v0 cos a ; vy = v0 sin a ; vy = -gt +v0 sin a ; La position est une primitive de la vitesse : x = v0 cos a t+constante. y = -½gt2 +v0 sin a t+ constante. A l'instant initial : x0 = 0 ; x = v0 cos a t ; y0 = h ; y = -½gt2 +v0 sin a t+ h. Q9. Montrer que l’équation de la trajectoire du centre de masse M du hobbyhorseur s’écrit sous la forme : y(x) = - g/(v02 cos2(a)∙ x2 + tan(a) ∙ x + h. t = x/ ( v0 cos a ).  Repport dans y : y = -½gx2 / ( v0 cos a )2.+x tan a + h. Données : - à l'instant initial, le hobbyhorseur se trouve au point M(t=0) tel que OM(t=0) = h = 1,19 m ; - la distance D entre le point O et la base du support de la barre d’obstacle horizontale à franchir est D = 50,0 cm ; - les jambes du hobbyhorseur sont repliées au maximum lors du saut et occupent un espace de 30 cm en-dessous de son centre de masse M ; La trajectoire du centre de masse M du hobbyhorseur est modélisée par l’équation suivante, avec les coordonnées x et y exprimées en m : y(x) = - 0,590 x2 + 0,566 x + 1,19. Q10. Déterminer si le hobbyhorseur franchira ou non la barre d’obstacle horizontale, placée à une hauteur H = 1,00 m du sol. x = D = 0,50 m ; y(0,5) =- 0,590 *0,52 + 0,566 *0,5 + 1,19~1,33 m. 1,33-0,30=1,03 m > 1,0 m : l'obstacle est franchi. Pour la question suivante, le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée Q11. À l’aide des données, calculer la valeur de l’angle a puis celle de la valeur de la vitesse initiale v0 avec lesquelles le hobbyhorseur aborde l’obstacle. Indiquer comment le hobbyhorseur peut faire évoluer ces paramètres pour modifier sa trajectoire afin de sauter une barre d’obstacle de hauteur plus élevée. tan a = 0,566 ; a ~29,5 °. -½g / ( v0 cos a )2.= -0,590. 4,905 / (0,87 v0)2 = 0,590 ; (0,87 v0)2 =4,905 / 0,590  =8,31 ; v02 =8,31 /0,872 =10,98 ; v0 = 3,31 m /s. y = -½gx2 / ( v0 cos a )2.+x tan a + h. Pour une valeur de x donnée : pour augmenter h, il faut augmenter v0 et dans une moindre mesure augmenter l'angle a. 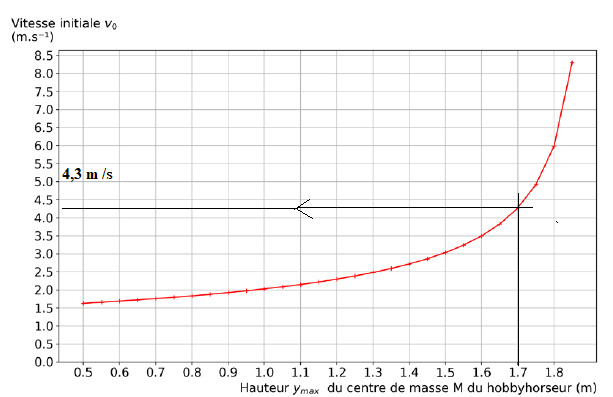Le hobbyhorseur réalise un deuxième saut. La figure  représente l’évolution de la vitesse initiale v0 en fonction de la hauteur maximale ymax du centre de masse M du même hobbyhorseur avec un angle a' par rapport au sol de 55°, une distance D de valeur égale à 50,0 cm ainsi qu’une hauteur initiale telle que OM(t=0) = h = 1,19 m. Le record du monde de saut d’obstacles en hobby horse a été établi à une hauteur d’obstacle de 1,40 m en 2019 par Marie Karkkainen lors du championnat du monde de la discipline en Finlande. Q12. À partir de la figure , déterminer la valeur de la vitesse initiale v0 avec laquelle le hobbyhorseur doit arriver sur l’obstacle pour espérer égaler le record mondial. Indiquer si cela est réalisable par ce hobbyhorseur sachant qu’habituellement lors des entraînements, sa vitesse initiale v0 est comprise entre 11,5 et 13,5 km∙h–1. Position du centre de masse 1,40 +0,30 ( longueur des jambes repliées) = 1,70 m 4,3 x3,6 ~15,5 km / h, valeur supérieure à ces vitesses d'nentraînement. Il ne pourra pas égaler le record.

menu