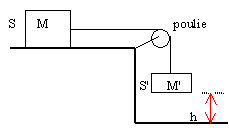
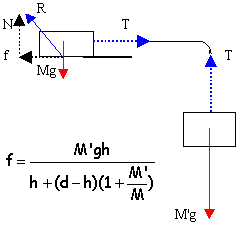
th de l'énergie cinétique - travaild'une force cours exercices En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. ..
. .
Dans un repère galiléen, la variation d'énergie cinétique(J) d'un solide entre 2 instants est égale à la somme des travaux des forces extérieures appliquées durant cet intervalle de temps	le travail d'une force constante ne dépend que des positions de départ et d'arrivée, peu importe le chemin suivi.
travail du poids sur le trajet A B mg(hA- hB) avec h=altitude quand on monte le travail du poids est négatif	la force magnétique, perpendiculaire au vecteur vitesse ne travaille pas.
travail de la force électrique sur le trajet AB charge* tension UAB
exercice 1 balle et rebond Une balle de masse m=100g est lachée sans vitesse d'une hauteur h=1 m. g=9,8 ms-2. La balle rebondit sur le sol. L'énergie cinétique juste après le rebond est égale à l'énergie cinétique juste avant multipliée par une constante k=0,9. Quelle est la vitesse de la balle juste après un rebond ? Quelle est l'altitude maxi atteinte après un rebond ? Quelle est la durée de la seconde descente ? Reprendre les deux questions précédentes mais après le 5 ème rebond. corrigé juste avant le premier rebond l'énergie potentielle initiale est sous forme cinétique 0,5 mv²=mgh =0,1*1*9,8=0,98 J juste après le premier rebond l'énergie cinétique vaut 0,98*0,9= 0,882 J d'où la vitesse après rebond: v²=0,882*2/0,1 ; v=4,2 ms-1. à l'altitude maximale après rebond l'énergie se trouve sous forme potentielle. 0,882=mg h' ; h'=0,882/(0,1*9,8)= 0,9 m durée de la chute libre lors de la seconde descente h'=0,5*9,8 t² ; t²=0,9/4,9 ; temps =0,428 s au dela du 5 ème rebond énergie cinétique juste aprés ce 5ème rebond = E initiale fois 0,95. 0,98*0,95=0,578 J d'où la vitesse v²=0,578*2/0,1=11,56 ; v=3,4 ms-1. 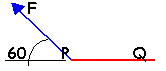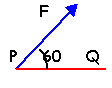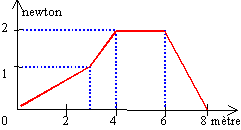altitude= altitude de départ *0,9 5 = 0,59 m ou bien 0,578=mgh durée: 0,59=0,5*9,8 t² ; t=0,346 s exercice 2 travail d'une force quelconque On considère une force F, (sa valeur ne dépend que de la distance x),de direction et de sens constants. Sous l'action de cette force une particule se déplace parallèlement à la force de P en Q. Le schéma donne les variations de la valeur de F en fonction de la distance. Quel est la valeur du travail de F au cours du déplacement?2 J ; 4 j ; 9 J ; 16 J. Une force constante de valeur 5N travaille sur une distance PQ=35 cm de P vers Q. Le travail de cette force est égal à -1,51 J. Quel schéma correspond à cette valeur ? corrigé La valeur de la force ne dépend que de la distance x; le travail est égal à l'aire de la surface comprise entre la courbe et l'axe des x. La lecture sur le graphe donne 9J Le travail d'une force constante est égale au produit scalaire du vecteur force par le vecteur déplacement. 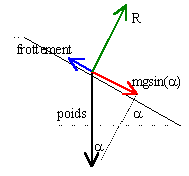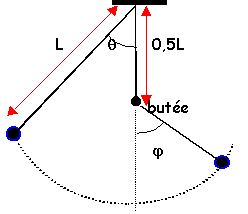valeur de la force (N)fois valeur du déplacement (m)fois cosinus de l'angle de ces deux vecteurs (1) donne 5*0,35 cos(60) =0,875 J (2) donne 5*0,35 cos(150) = -1,51 J (3) donne 5*0,35 cos(120) = -0,875 J exercice 3 un pendule et une butée longueur L=1 m ; angle q=45° ; m=100 g ; on lache le pendule sans vitesse initiale. Les frottements son négligés. Quelle est l'amplitude angulaire jmax du coté droit de la figure ? Que devient jmax si l'angle q est divisé par deux ? Quelle est la période de ce pendule ? Quelle est la vitese maxi au passage à la verticale ? corrigé A l'amplitude angulaire, l'énergie du pendule est sous forme potentielle de pesanteur. L'énergie se conserve en l'absence de frottements. L'altitude maxi à droite est égale à l'altidude maxi à gauche. Origine des altitudes: point le plus bas. L(1-cos(45)) = 0,5L(1-cos(jmax)) 1-cos(45) = 0,5(1-cos(jmax)) cos(jmax)=(cos(45)-0,5)*2=0,414 ; jmax=65,5° si l'angle q est divisée par 2 : cos(jmax)=(cos(22,5)-0,5)*2=0,848 ; jmax=32° Période de ce pendule période (s)= 2*3,14 fois rac. carrée(longueur(m)/ 9,8) à gauche de la verticale: longueur =L=1m , à droite longueur=0,5 m longueur période durée mvt à gauche 1 2 0,5 à droite 0,5 1,42 0,355 période :2( 0,5+0,354)=1,71 s Au passage à la verticale, l'énergie est sous forme cinétique et la vitesse est maximale 0,5 m v²max= énergie potentielle de départ =mgL(1-cos(45)) v²max=2*gL(1-cos(45))=5,74 ; vmax=2,39 ms-1. 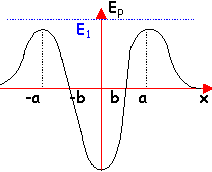exercice 4 diagramme énergétique Un mobile a une trajectoire rectiligne suivant Ox. Il est soumis à des forces telles que son énergie mécanique reste constante. Le graphe ci contre représente son énergie potentielle en fonction de x. Dans les trois 1ère questions l'énergie mécanique vaut E1 et elle est nulle à la 4 ème question. Pour quell(s) abscisse(s) la vitesse est-elle maxi ? Lorsque le mobile est très loin de l'origine des axes, la vitesse est elle nulle ?. Dans quel intervalle le mobile ralentit. Sur quel intervalle se déplace le mobile? corrigé L'énergie mécanique est la somme de l'énergie cinétique (liée à la vitesse) et de l'énergie potentielle. En conséquence, la vitesse est maxi si l'énergie potentielle est minimale; x=0 Très loin de l'origine O, l'énergie potentielle est nulle et l'énergie cinétique vaut E1.En conséquence, la vitesse n'est pas nulle. Si la vitesse diminue , l'énergie cinétique diminue et l'énergie potentielle augmente. ] -infini; -a] et [0 ; a[ La somme des énergies cinétique et potentielle est nulle et de plus l'énergie cinétique est toujours positive. Ep+Ec=0 ; Ep=-Ec avec Ec positive. l'énergie potentielle est négative et le solide se déplace sur [-b ; +b]. exercice 5 lancer vertical Une flèche de masse 25g est lancée verticalement vers le haut à partir d'un poit A situé à 1,8 m au dessus du sol, avec une vitesse de 12 ms-1. En absence de frottement la hauteur maximale atteinte est de: 6,73 m ;9,15 m ; 10,42 m ; 7,35 m ; 24,3 m. corrigé   Energie mécanique au départ (le sole est l'origine des altitudes): 0,5 m v2 +mgh0 Energie mécanique au point le lus haut (vitesse nulle): mghmax L'énergie mécanique se conserve : 0,5 m v2 +mgh0=mghmax soit 0,5 v2+gh0=ghmax hmax=h0+0,5 v2 /g = 1,8+0,5*144/9,8=9,15 m exercice 6 plan incliné avec frottement Un solide de masse m =200g descend un plan AB=50 cm incliné d'un angle a =30°sur l'horizontale .Au passage en A sa vitesse est 2 ms-1 et en B 2,83 ms-1 . La force de frottement a une valeur constante g=10ms-2. La direction du vesteur accélération est verticale (répondre vrai ou faux) La valeur de l'accélération du solide est 1 ms.-2 La valeur de la force de frottement est 0,2 N Du fait de la force de frottement le solide finira par s'arrêter corrigé Lors d'une chute libre, l'accélération est verticale . Ici l'accélération est parallèle au plan , dirigée vers le bas V2B - V2A =2*accélération*AB (V2B - V2A) / (2AB) a =4 ms-2 suivant la ligne de plus grande pente , la seconde loi de Newton s'écrit : -f+mgsin(a)=ma d'où f=m(gsin(a)-a) 0,2*(10*0,5-4) f=0,2N Le solide ne peut s'arrêter sous l'effet des frottements ; ces derniers restent inférieurs à mgsin(a) . D'autre part la vitese augmente lors de la descente . 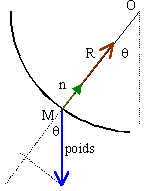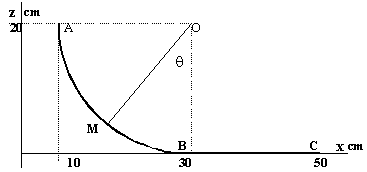exercice 7 solide sur une piste verticale incurvée - frottements Un solide S,de masse m=500g glisse sur une piste ABC située dans un plan vertical. La partie Ab est un quart de cerclede rayon r=20cm. Sur cette partie AB les frottements sont négligeables. La partie BC est horizontale et BC=20 cm. Le mobile part de A sans vitesse initiale, il descnd et s'immobilise en C la vitesse en A est égale à 7,12 km h-1. l'expression de la vitesse au carrée en M est égale à : 2g OA cos(q) si q=20° , l'action du support en M est 13,8 N En supposant la force de frottement constante sur la partie BC, on peut en déduire que sa valeur est 5000N corrigé vrai la variation d'énergie cinétique entre A et B est égal au travail du poids (l 'action du plan , perpendiculaire au plan ne travaille pas) 0,5 mv2B=mg OB ; v2=2gOB=2*9,8*0,2 ; v=7,12 km h-1 vrai entre A et M l'énergie mécanique se conserve. mgOA=mgOA(1-cos(q))+0,5 mv2M v2M=2g*OA cos(q) vrai écrire la 2ème loi de Newton suivant l'axe n de la base de Frenet -mgcos(q)+R= mv2M / OA remplacer v2M par l'expression ci dessus R=3mgcos(q)=13,8 N faux entre B et C seul les frottements travaillent ; la variation d'énergie cinétique est égale au travail des frottements -0,5mv2B= -f* BC f=0,5*0,5*1,982 /0,2=4,88 N 1 m s-1 =3,6 km h-1 exercice 8 mouvement sur deux plans inclinés 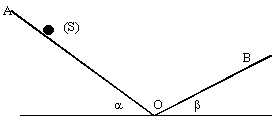Un solide S assimilable à une masse ponctuelle m=50g glisse sans frottement sur deux plaques inclinées. La rupture de pente n'entrîne pas de perte d'énergie mécanique . S est laché sans vitesse initiale. L'altitude de A , notée hA est supérieure à celle de B. Si S est laché de A, sa vitesse au point O est Laché de A, le temps mis par S pour arriver en O est indépendant de sa masse m. Si S est laché de B, le système(solide pesant et plans inclinés) est un oscillateur mécanique. 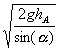Si S est laché de A, le système(solide pesant et plans inclinés) est un oscillateur mécanique corrigé faux l'énergie mécanique en A est mghA=mg OA sin(a) l'énergie mécanique en O est 0,5 mv2 l'énergie mécanique se conserve v2=2ghA=2g OA sin(a) faux la masse intervient dans l'expression de l'énergie cinétique ou potentielle. l'accélération de S est gsin(a); la durée du parcours OA est indépendante de la masse. La 3 ème affirmation est exacte, l'altitude de B est inférieure à celle de A et au départ il n'y a pas de vitesse. La 4 ème affirmation est fausse, l'altitude de A est supérieure à celle deB; arrivé en B le solide quitte le plan et tombe en chute libre. exercice 9 Déterminer une force de frottement fil inextensible et sans masse. Poulie sans frottement et masse négligeable. S'chute d'une hauteur h et S glisse d'une distance d avant de s'arrêter. vitesse départ nulle. Les frottements sont supposés constants sur le plan horizontal. Ecrire le th. de l'énergie cinétique pour le système {S , fil et S'}. Exprimer la valeur de la force de frottement f en fonction de M, M',d ,h, g Calculer f si M=1 kg; M'=5 kg; h=0,1 m; d=0,3 m; Calculer la vitese maxi atteinte. calculer l'accélération (1ère phase du mouvement) Calculer la tension du fil. corrigé parcours h : variation énergie cinétique : 0,5 (M+M')v² travaux des forces : -f h + M'gh 0,5 (M+M')v²= -f h + M'gh (1) parcours d- h : variation énergie cinétique : - 0,5 Mv² travaux des forces : -f ( d-h) - 0,5 Mv² = -f ( d-h) (2) f=3,84 N. V²= 2f / M (d-h) d'où Vmaxi= 1,24 ms-1. a =V²/(2h) = 7,68 ms-2 2 ème loi de Newton appliquée à S sur un axe horizontal -f + T= Ma T = Ma + f = 11,5 N   retour - menu