En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
..
..
| .
. |
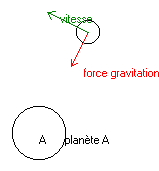
accélération = champ de gravitation à l'altitude considérée
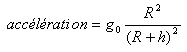
![]()
![]()
![]()
|
|
|
||||||||||||||
|
Un satellite de la terre décrit une orbite circulaire dans le plan de l'équateur terrestre. Sa période est notée T. L'altitude du satellite est 640 km : rayon terrestre R=6400 km ; g=9,8 ms-2 . Le mouvement du satellite est uniforme (répondre vrai ou faux) Si l'altitude double, alors T2 est multipliée par 2 1/3. La vitesse du satellite
sur sa trajectoire est : La période du satellite est supérieure à 1 heure |
|||||||||||||||
|
|
|||||||||||||||
|
|
|
||||||||||||||
|
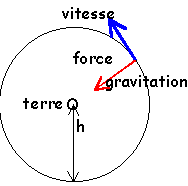
La norme du vecteur vitesse est constante, donc le mouvement est uniforme
La circonférence de rayon R+h= 7,04 106 est parcourue à la vitesse v pendant T seconde. |
|||||||||||||||
|
|
|
||||||||||||||
|
|
 |
||||||||||||||
|
|||||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
||||||||||||
|
vrai il tourne avec la même vitesse angulaire que la terre et paraît fixe pour un observateur terrestre. vitesse angulaire (rad s-1)=2 *3,14 divisé par la période (s) 6,28/8,6 104 vrai voir la 3 ème loi de Kepler rayon3=(8,6 104)2 /10-13 faux c'est un relais pour les télécommunications car il paraît fixe pour un observateur terrestre. |
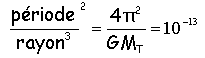 |
||||||||||||||
|
|
|||||||||||||||
|
|
|
||||||||||||||
|
Loi des périodes : les carrés des temps de révolution des planètes sont proportionnels aux cubes des grands axes des orbites.
|
|||||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
||||||||||||
La force n'est pas changée car toutes les distances sont comptées à partir du centre de la planète, la masse étant ramenée au centre (corps à symétrie sphérique)
Les forces de gravitation sont proportionnelles aux masses des planètes (donc 95 fois plus grande pour saturne) et inversement proportionnelles aux carrés des distances (donc 905² fois plus petite pour saturne) 95 / 905²=1,16 10-4 |
|||||||||||||||
|
|
|||||||||||||||
|
|
|
||||||||||||||
|
|||||||||||||||
|
|
|||||||||||||||
|
|
|
||||||||||||||
|
vitesse ms-1 = w*rayon m accélération centripète ms-2 = w² rayon
|
|||||||||||||||
|
|
|||||||||||||||
|
|||||||||||||||
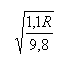
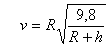 R+h=6400+640=1,1R ;
v=6,4
106*1,179 10-3
=7551
ms-1 =2097 kmh-1.
R+h=6400+640=1,1R ;
v=6,4
106*1,179 10-3
=7551
ms-1 =2097 kmh-1.
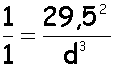 d=9,54
u.a
d=9,54
u.a