|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. ..
.. |
||||||||||||||||
|
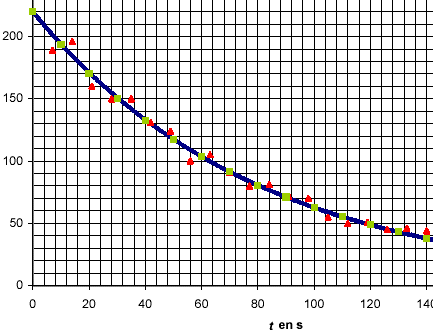
Courbe de décroissance radioactive par la méthode d'Euler : Le professeur propose à l'élève d'obtenir un ensemble de points qui modélise cette décroissance en utilisant la méthode d'Euler. Pour cela on note m(t) le nombre d'évènements détectés à la date t et m(t+Dt) celui qui correspond à la date t + D t et on écrit m(t+Dt) - m(t) = D m . Dt est appelé "pas de résolution" de la méthode d'Euler. On fait l'hypothèse que le radon 220 est seul responsable de la radioactivité de l'échantillon. On en déduit que D m est proportionnel à la fois à m(t) et à D t ; la constante de proportionnalité est -l avec l = 0,0125 s-1 constante radioactive du radon 220. Prendre pour valeur à l'origine la valeur m0 = 220 évènements détectés par seconde.
Dm= -l m Dt. La durée de l'étude est t =140 s, l'ordre de grandeur d'un pas souhaitable est t/100. La valeur la plus proche est 0,5 s. 1 µs est un pas trop petit, la durée du calcul serait trop grande. Avec 20 s le pas serait trop grand et le résultat non satisfaisant. (peu de points pour tracer une courbe ) à t=0 : meuler (0) = 220 Dm= -l m Dt = -0,0125*220*0,5 = -1,375 m(0+Dt) = m(0) + D m = 220-1,375 = 218,625 soit 219. à t=0,5 : meuler (0,5) = 218,625 Dm= -l m Dt = -0,0125*218,625*0,5 = -1,366 m(0,5+Dt) = m(0,5) + D m = 218,625-1,366 = 217,259 soit 217. Les points obtenus avec la méthode d.Euler sont compatibles avec les points expérimentaux. L'hypothèse du 3. paraît acceptable : le radon 220 est bien le seul responsable de la radioactivité de l'échantillon. dm / dt = -l m soit dm/dt + l m=0 m = m0 e-lt ; dm/dt = -l m0 e-lt repport dans l'équation différentielle : -l m0 e-lt + lm0 e-lt = 0 quel que soit t t=0 : mth = m0 =220. t = 10s : mth = 220 e (-0,0125*10) = 194,14 ( 194) t = 20s : mth = 220 e (-0,0125*20) = 171,33 ( 171) les points mth coincident avec les points meuler. La méthode d'Euler permet de trouver une solution approchée de l'équation différentielle. La méthode d'Euler nécessite de connaître les conditions initiales ainsi qu'une relation entre la grandeur étudiée et sa variation. |
||||||||||||||||
|
|