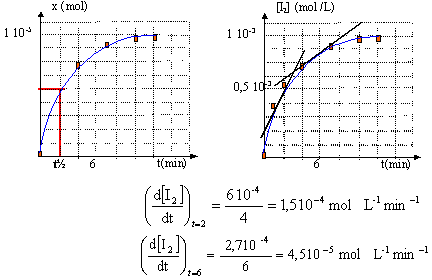|
chimie bac :
transformations chimiques : spectrophotométrie
fiche
bac
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
..
..
|
|
oxydation d'un
alcool :
Dans un bécher, introduit : 50 mL d'une solution
de permanganate de potassium de concentration 0,20 m/L et 50
mL d'une solution d'acide sulfurique de concentration 2,0
mol/L. Puis mettre sous agitation. Prélever 1,0 mL de
propan-2-ol pur ; à la date t=0 (déclencher le
chronomètre), ajouter l'alcool au contenu du
bécher.
Prélever rapidement un volume V=10 mL du
mélange contenu dans le bécher et l'introduire
dans un petit bécher. Renouveler 8 fois cette
opération pour préparer huit petits
béchers. A la date t1=1 minute, ajouter
rapidement au contenu de l'un des béchers environ 40
mL d'eau glacée (cela s'appelle une trempe). Titrer
les ions permanganate restant par une solution de sulfate de
fer (II) de concentration c'=0,50 mol/L. Relever le volume
équivalent v'éq.
Recommencer les opérations
précédentes aux différentes dates
indiquées dans le tableau ci-dessous.
Le tableau ci-dessous regroupe les résultats des
différents titrages : v'éq est le volume de
solution d'ions fer (II) ajouté à
l'équivalence.
|
t(min)
|
1
|
2
|
3
|
4
|
6
|
10
|
15
|
20
|
|
v'éq(mL)
|
8,6
|
7,8
|
7,4
|
6,9
|
6,3
|
5,6
|
5,2
|
5
|
- Ecrire l'équation de réaction (1)
d'oxydation du propan-2-ol par les ions
permanganate.
- Ecrire l'équation de la réaction (2)
entre les ions de fer (II) et les ions permanganate, qui
sert, de support au titrage.
- Dresser le tableau d'évaluation de la
réaction (2). En déduire l'expression de n
= nMnO4-(aq) , quantité d'ions
permanganate restant à la date t dans les 100 mL
du mélange réactionnel, en fonction de c'
et v'éq . Regrouper les
résultats sous forme d'un tableau.
- Dresser le tableau d'évolution de la
réaction (1). En déduire une relation qui
exprime l'avancement x en fonction de n =
nMnO4-(aq) et n0, quantité
initiale d'ions permanganate. Calculer x à chaque
date. Regrouper les résultats dans un
tableau.
- Tracer la représentation graphique
x=f(t).
- Quel est le réactif limitant dans la
réaction (1) ? Que vaut l'avancement maximal de
cette réaction supposée totale ?
Déterminer le temps de demi-réaction.
- Comment préparer un volume de 500 mL des
solutions de permanganate de potassium et de sulfate de
fer (II) ?
- Quel intérêt d'effectuer une trempe
avant de faire les titrages ? Comment détecter
l'équivalence ?
Données : * propan-2-ol :
CH3-CHOH-CH3 Densité=d=0,8
masse molaire :M=64g/mol
* permanganate de potassium : KMnO4 masse
molaire : M=158g/mol
* sulfate de fer (ll) hydraté : FeSO4
,5H2O masse molaire M=242 g/mol.
* couples oxydant/réducteur qui intervient :
Fe 3+ (aq) / Fe 2+ (aq) ;
MnO4 -(aq) / Mn2+(aq)
CH3 -CO-CH3 /
CH3-CHOH-CH3
corrigé
5 fois { CH3-CHOH-CH3
-->CH3 -CO-CH3 + 2H+ +
2e- }oxydation
2 fois { MnO4 -+8H+ +
5e- -->Mn2++ 4H2O }
réduction
5 CH3-CHOH-CH3
+2MnO4 -+6H+ -->
5CH3 -CO-CH3 +2Mn2++
8H2O (1)
Fe 2+ -->Fe 3+ + e-
oxydation
MnO4 -+8H+ +5 Fe
2+ -->5Fe 3+ +2Mn2++
4H2O (2)
|
5 Fe 2+ ajouté
|
MnO4 -
|
|
t=0
|
0
|
n
|
|
t
|
c' v
|
n-c'v/5
|
|
équivalence
|
c'véq
|
0= n-c'véq/5
|
d'où n = 0,2 c'véq mmol dans 10 mL
si le volume est en mL et c' en mol/L.
et dans 100 mL de solution : n= 2 c'véq
= 2*0,5 véq =
véq mmol.
alcool : 1mL donc 0,8 g soit 0,8 / 64 = 0,0125 mol = 12,5
mmol
MnO4 - : n0 =50 * 0,2 =
10 mmol initial
|
5 alcool
|
2MnO4 -
|
|
t=0
|
12,5 mmol
|
n0=10
|
|
t
|
12,5-5x
|
n0- 2x=10-2x
|
|
équivalence
|
12,5-5xmax
|
10-2xmax
|
d'oùxmax = 12,5/5 = 2,5 mmol ( alcool en
défaut), réactif limitant
à la date t : n0- 2x = véq
(mmol) soit x = (véq
-n0) / 2 mmol.
|
t(min)
|
1
|
2
|
3
|
4
|
6
|
10
|
15
|
20
|
|
x mmol
|
0,7
|
1,1
|
1,3
|
1,55
|
1,85
|
2,2
|
2,4
|
2,5
|
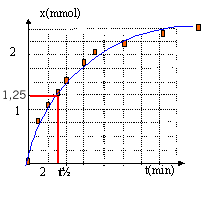
t½ voisin de 3 min, durée au bout de laquelle
l'avancement est égal à la moitié de
l'avancement final
préparer 500 mL de chaque solution :
0,1 mol permanganate de potassium dans 0,5 L donc peser :
158*0,1 = 15,8 g de solide puis dissoudre dans l'eau .
0,25 mol sulfate de fer dans 0,5 L donc peser 242*0,25 =
60,5 g de solide.
trempe : on réalise un blocage
cinétique de la réaction (1) ce qui nous
laisse le temps de doser les ions permanganate restant.
les ions permanganate jouent un double rôle :
réactif et indicateur de fin de réaction :la
couleur de la solution passe de du violet à
l'incolore à l'équivalence. ( solution de
sulfate de fer dans la burette)
|
|
réduction du diiode par
le zinc :
On plonge une lame de zinc dans une solution de diiode de
concentration c=0,02 mol/L et de volume V=200mL. Le zinc
appartient au couple Zn2+ (aq) / Zn (s) et le
diiode au couple I2 (aq) / I- (aq)
.
- Ecrire l'équation de la réaction
d'oxydoréduction qui se produit quand on met en
présence le zinc et le diiode.
- Dans une expérience préliminaire, on
étalonne un spectrophotomètre avec des
solutions étalon de diiode de concentration
connue. Soit A l'absorbance. Les résultats sont
regroupés dans le tableau
ci-dessous.
|
c( mol/L)
|
2 10-4
|
5 10-4
|
8 10-4
|
10 10-4
|
12 10-4
|
|
A
|
0,21
|
0,55
|
0,88
|
1,1
|
1,32
|
-Tracer la représentation graphique A= f ( c )
-Trouver l'équation de cette représentation
graphique.
-Quelle est l'utilité de cette expérience
préliminaire ?
- Pour étudier la cinétique de la
réaction, on prélève 5,0 mL du
mélange réactionnel que l'on place dans une
fiole jaugée de 100 mL. Aux dates t
indiquées dans le tableau ci-dessous, on ajoute de
l'eau distillée glacée dans la fiole
jusqu'au trait diluée et on la place dans le
spectrophotomètre. On mesure l'absorbance A de la
solution diluée.
|
t(s)
|
0
|
30
|
60
|
100
|
200
|
300
|
400
|
600
|
800
|
1000
|
1200
|
1400
|
|
A
|
1,1
|
0,88
|
0,77
|
0,67
|
0,52
|
0,42
|
0,35
|
0,24
|
0,17
|
0,12
|
0,1
|
0,08
|
- Déterminer pour chaque valeur de t, la
concentration du diiode dans la solution
diluée.
- En déduire la concentration du diiode dans le
mélange réactionnel à chaque date
t.
- Dresser le tableau d'évolution du système
chimique au cours de la transformation.
- En déduire la valeur de l'avancement x à
chaque date t (regrouper les résultats dans un
tableau).Remarque : Le zinc est en grand
excès.
- Tracer la représentation graphique x=f(t).
- Déterminer le temps de demi-réaction
sachant que la transformation est totale.
- Evaluer la vitesse de réaction aux dates t=100s
et t=500s. Conclure sur l'évolution de cette
vitesse de réaction.
corrigé
Zn (s) + I2 (aq) à Zn2+
(aq) + 2I- (aq)
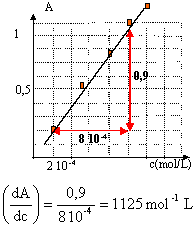
étalonage du spectrophotomètre.
c = A / 1125 mol/L ou bien A= 1125 c.
en tenant compte du facteur de dilution : 100 / 5 = 20,
[I2]= 20A/1125 = 0,018 A
|
t(s)
|
0
|
30
|
60
|
100
|
200
|
300
|
400
|
600
|
800
|
1000
|
1200
|
1400
|
|
[I2] mol/L
|
20 10-3
|
16 10-3
|
13,6 10-3
|
12 10-3
|
9,2 10-3
|
7,4 10-3
|
6,2 10-3
|
4,2 10-3
|
3 10-3
|
2,2 10-3
|
1,8 10-3
|
1,4 10-3
|
Qté diiode initial : 20 10-3 *0,2 = 4
10-3 = 4 mmol
|
Zn
|
I2
|
Zn2+
|
2I-
|
|
initial
|
excès
|
4 10-3 mol
|
0
|
0
|
|
en cours
|
|
4 10-3 -x
|
x
|
2x
|
|
fin
|
|
4 10-3
-xmax=0
|
4 mmol
|
8 mmol
|
xmax= 4 10-3 mol = 4 mmol
4 10-3 -x = nI2 avec nI2
=[I2] * 0,2
4 10-3 -x =[I2] * 0,2 soit
x = 4 10-3 -[I2] * 0,2
|
t(s)
|
0
|
30
|
60
|
100
|
200
|
300
|
400
|
600
|
800
|
1000
|
1200
|
1400
|
|
x mol
|
0
|
0,8 10-3
|
1,3 10-3
|
1,6 10-3
|
2,2 10-3
|
2,5 10-3
|
2,8 10-3
|
3,2 10-3
|
3,4 10-3
|
3,56 10-3
|
3,64 10-3
|
3,72 10-3
|
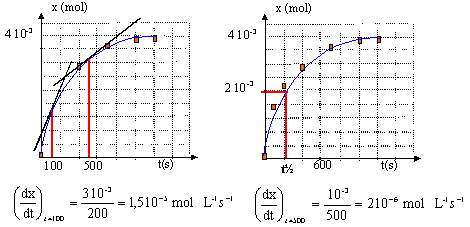
t½ voisin de 200 s, durée au bout de laquelle
l'avancement est égal à la moitié de
l'avancement final
la vitesse de la réaction ( coefficients
directeurs des tangentes à la courbe) diminue au
cours du temps car les concentrations des réactifs
diminuent.
|
|
cinétique de la
réaction des ion iodure avec l'eau
oxygénée :
L'ion iodure est le réducteur du couple
I2 (aq) / I- (aq). L'eau
oxygénée, ou peroxyde d'hydrogène
H2O2, est l'oxydant du couple
H2O2 (aq) / H2O.
- Ecrire l'équation de la réaction
d'oxydoréduction entre les ions iodure et l'eau
oxygénée en milieu acide.
- Pour suivre la cinétique de la
réaction, on commence par étonner le
spectrophotomètre avec des solutions de diiode de
concentration c connue. Les résultats sont
regroupés ci-dessous.
|
c mol/L
|
1 10-4
|
2 10-4
|
4 10-4
|
6 10-4
|
8 10-4
|
10 10-4
|
|
A
|
0,188
|
0,378
|
0,749
|
1,128
|
1,501
|
1,878
|
- Tracer le représentation graphique A=f (c).
- Trouver son équation.
- La loi de Beer-Lambert est-elle vérifiée
?
- Pour étudier la réaction, on
opère de la façon suivante.
- On prépare, dans un bécher, un volume
v1 = 5,0 mL d'une solution S1
d'iodure de potassium de concentration c1=0,02
mol/L, auquel on ajoute 1 cristal de chlorure de fer
(II). Les ions fer (II) permettent
d'accélérer la réaction car les
concentrations sont faibles. Ils n'intervient pas dans
l'équation de la réaction.
- Dans un autre bécher, on place un volume
v2=5,0 mL d'une solution S2 d'eau
oxygénée acidifiée de concentration
c2=2,0 x10-3 mol/L.
- A la date t=0, on mélange les contenus des 2
béchers et agite. Très rapidement, on place
une partie du mélange dans une cuve que l'on
introduit dans le spectrophotomètre. On relie le
spectrophotomètre à un ordinateur et on
obtient la courbe ci-dessous.
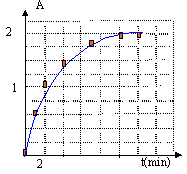
- Déduire de cette courbe, la
représentation graphique
[I2(aq)]=f(t) (on travaillera sur une
dizaine de points).
- Quel est la réactif limitant ?
- Dresser le tableau d'évolution du système
chimique.
- Dans la cuve du spectrophotomètre, la
réaction avance de la même façon que
dans le milieu réactionnel. Déterminer
l'avancement x de la réaction en fonction de
[I2 (aq)] et de
V=v1+v2, volume total du
mélange réactionnel. Calculer x pour les
mêmes points que ceux utilisés dans la
question 3.
- Tracer la représentation graphique x=f(t).
- Déterminer le temps de dem-réaction.
- Evaluer la vitesse de réaction aux dates t=2.0
minutes et t=6.0 minutes.
- Interpréter l'évolution de la
vitesse.
corrigé
2I--->I2+2e-
oxydation
H2O2 + 2H+
+2e---> 2H2O réduction
H2O2 + 2H+
+2I--->I2+2H2O
|
c mol/L
|
1 10-4
|
2 10-4
|
4 10-4
|
6 10-4
|
8 10-4
|
10 10-4
|
|
A
|
0,188
|
0,378
|
0,749
|
1,128
|
1,501
|
1,878
|
|
A/c
|
1880
|
1890
|
1872
|
1880
|
1876
|
1878
|
absorbance et concentration du diiode sont proportionnelles
: la loi de Beer-Lambert est vérifiée.
A= 1880 c
à l'instant initial, les quantités de
matière sont :
ion iodure : 0,02* 5 10-3 = 10-4
mol
eau oxygénée : 2 10-3 * 5
10-3 = 10-5 mol
|
H2O2
|
2I-
|
I2
|
|
initial
|
10-5 mol
|
10-4 mol
|
0
|
|
en cours
|
10-5 -x
|
10-4 - 2x
|
x
|
|
fin
|
10-5 -xmax=0
|
10-4 - 2xmax
|
xmax=10-5
mol
|
H2O2 est le réactif
limitant.
à partir de la courbe A=f(t) on obtient
[I2]=f(t) en divisant l'absorbance A par
1880.
[I2]= x /
(v1+v2) = x / (5+5) 10-3 =
100 x d'où x = [I2]/100
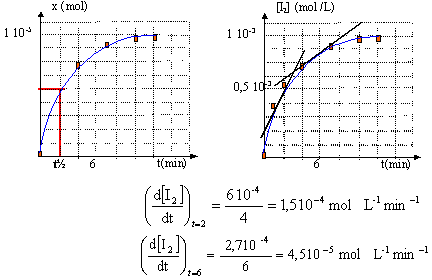
|
|
réduction du
diiode
Le " lugol " est une solution antiseptique à base
de diiode I2. Quand on plonge une lame de zinc
dans cette solution, on peut observer, au bout d'un temps
assez long, une décoloration et une attaque du zinc.
L'équation de la réaction est : Zn (s) +
I2 (aq) à Zn2+ (aq) +
2I- (aq)
Pour étudier cette réaction, on suit
l'évolution de la quantité de matière
de diiode présente en fonction du temps. Au bout de
cette expérience, la température est de
20°C. La concentration initiale du diiode est
c0=0,020 mol/L. On effectue 12
prélèvements de volume v0 = 20mL
que l'on place dans 12 béchers. A la date t=0, on
introduit, dans chaque bécher, deux morceaux de
grenaille de zinc (le diiode est alors le réactif
limitant). A chaque date indiquée dans le tableau
ci-dessous, on place rapidement un des béchers dans
la glace, puis on titre le diiode restant par une solution
de thiosulfate de sodium de concentration c=0,020 mol/L.
L'équation de la réaction de titrage est :
2S2O32- (aq) +
I2 (aq) -->
S4O62-(aq)+ 2I-
(aq).
Les résultats des titrages sont indiqués
dans le tableau ci-dessous où véq
représente le volume de sodium de thiosulfate de
sodium versé à
l'équivalence.
|
t(s)
|
30
|
60
|
100
|
200
|
300
|
400
|
600
|
800
|
1000
|
1200
|
1400
|
1600
|
|
véq(mL)
|
31,6
|
27,4
|
24,2
|
19
|
15,2
|
12,5
|
8,4
|
5,8
|
4,2
|
3,2
|
2,6
|
2,2
|
- Calculer la quantité de matière
initiale de diiode notée n0.
- Exprimer nI2(aq), quantité de
matière de diiode à la date t en fonction
de c et de véq. Calculer
nI2(aq), à chaque date. Regrouper les
résultats sous forme d'un tableau.
- Dresser le tableau d'avancement de la
réaction. En déduire une relation entre
nI2(aq) restant à la date t,
n0 et l'avancement x. Calculer x à
chaque date. Regrouper les résultats sous forme
d'un tableau.
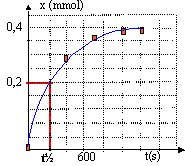
- Tracer la représentation graphique
x=f(t).
- Le diiode est le réactif limitant. Calculer
l'avancement maximal, en déduire le temps de
demi-réaction.
- On a placé les béchers dans la glace
avant d'effectuer le titrage. Comment appelle-t-on cette
opération ?
- Le thiosulfate de sodium est hydraté. Sa
formule est Na2S2O3,
2H2O. Quelle masse de solide a-t-il fallu pour
préparer 500 mL de solution de concentration 0,020
mol/L ?
-Faire le schéma annoté du montage qui sert
au titrage.Comment détecter l'équivalence
?
corrigé
n0 =0,02 * 20 10-3 = 4
10-4 mol.
|
2S2O32-
ajouté
|
I2
|
S4O62-
|
2I-
|
|
initial
|
0
|
nI2 mol.
|
0
|
0
|
|
en cours
|
c v = 0,02 v
|
nI2 - 0,01 v
|
0,01 v
|
0,02 v
|
|
équivalence
|
c véq = 0,02
véq
|
nI2 - 0,01
véq=0
|
0,01 véq
|
0,02 véq
|
à la date t , nI2 =
½ cvéq = 0,01 véq
|
t(s)
|
30
|
60
|
100
|
200
|
300
|
400
|
600
|
800
|
1000
|
1200
|
1400
|
1600
|
|
nI2 mmol
|
0,316
|
0,274
|
0,242
|
0,19
|
0,152
|
0,125
|
0,084
|
0,058
|
0,042
|
0,032
|
0,026
|
0,022
|
Zn (s) + I2 (aq) à Zn2+ (aq) +
2I- (aq)
|
Zn (s)
|
I2
|
|
initial
|
excès
|
n0
|
|
en cours
|
|
n0 -x = nI2
|
|
fin
|
|
n0 -xmax=0
|
x = n0 - nI2 = 0,4 -nI2
mmol
|
t(s)
|
30
|
60
|
100
|
200
|
300
|
400
|
600
|
800
|
1000
|
1200
|
1400
|
1600
|
|
x mmol
|
0,084
|
0,126
|
0,16
|
0,21
|
0,25
|
0,28
|
0,32
|
0,34
|
0,36
|
0,37
|
0,375
|
0,38
|
trempe ou blocage cinétique de la
réaction
préparer 500 mL de chaque solution :
0,1 mol thiosulfate de sodium dans 0,5 L
masse molaire : 2*23+2*32+3*16+2*18 = 194g/ mol
donc peser : 194*0,01 = 1,94 g de solide puis dissoudre
dans 0,5 L d'eau .
la burette contient la solution de thiosulfate de sodium
de concentration connue.
le bécher contient la solution de diiode à
doser + empois d'amidon ( en présence de diiode ,
l'empois d'amidon donne un couleur violette eintense)
agitateur magnétique.
retour
- menu
|
|